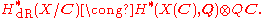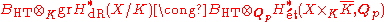P-adic Hodge theory
Encyclopedia
In mathematics
, p-adic Hodge theory is a theory that provides a way to classify and study p-adic Galois representations of characteristic 0
local field
s with residual characteristic p (such as Qp
). The theory has its beginnings in Jean-Pierre Serre
and John Tate
's study of Tate module
s of abelian varieties
and the notion of Hodge–Tate representation. Hodge–Tate representations are related to certain decompositions of p-adic cohomology
theories analogous to the Hodge decomposition, hence the name p-adic Hodge theory. Further developments were inspired by properties of p-adic Galois representations arising from the étale cohomology
of varieties
. Jean-Marc Fontaine introduced many of the basic concepts of the field.
of K) will be a continuous representation ρ : GK→ GL(V) where V is a finite-dimensional vector space
over Qp. The collection of all p-adic representations of K form an abelian category
denoted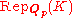
in this article. p-adic Hodge theory provides subcollections of p-adic representations based on how nice they are, and also provides faithful functors to categories of linear algebra
ic objects that are easier to study. The basic classification is as follows:
where each collection is a full subcategory properly contained in the next. In order, these are the categories of cristalline representations, semistable representations, de Rham representations, Hodge–Tate representations, and all p-adic representations. In addition, two other categories of representations can be introduced, the potentially cristalline representations Reppcris(K) and the potentially semistable representations Reppst(K). The latter strictly contains the former which in turn generally strictly contains Repcris(K); additionally, Reppst(K) generally strictly contains Repst(K), and is contained in RepdR(K) (with equality when the residue field of K is finite, a statement called the p-adic monodromy theorem).
by GK and some linear algebraic structure and to consider so-called Dieudonné modules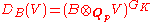
(where B is a period ring, and V is a p-adic representation) which no longer have a GK-action, but are endowed with linear algebraic structures inherited from the ring B. In particular, they are vector spaces over the fixed field
. This construction fits into the formalism of B-admissible representations
introduced by Fontaine. For a period ring like the aforementioned ones B∗ (for ∗ = HT, dR, st, cris), the category of p-adic representations Rep∗(K) mentioned above is the category of B∗-admissible
ones, i.e. those p-adic representations V for which
or, equivalently, the comparison morphism
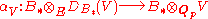
is an isomorphism
.
This formalism (and the name period ring) grew out of a few results and conjectures regarding comparison isomorphisms in arithmetic and complex geometry
:
To improve the Hodge–Tate conjecture to one involving the de Rham cohomology (not just its associated graded), Fontaine constructed a filtered ring BdR whose associated graded is BHT and conjectured the following (called CdR) for any smooth proper scheme X over K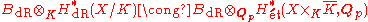
as filtered vector spaces with GK-action. In this way, BdR could be said to contain all (p-adic) periods required to compare algebraic de Rham cohomology with p-adic étale cohomology, just as the complex numbers above were used with the comparison with singular cohomology. This is where BdR obtains its name of ring of p-adic periods.
Similarly, to formulate a conjecture explaining Grothendieck's mysterious functor, Fontaine introduced a ring Bcris with GK-action, a "Frobenius" φ, and a filtration after extending scalars from K0 to K. He conjectured the following (called Ccris) for any smooth proper scheme X over K with good reduction
as vector spaces with φ-action, GK-action, and filtration after extending scalars to K (here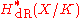
is given its structure as a K0-vector space with φ-action given by its comparison with crystalline cohomology). Both the CdR and the Ccris conjectures were proved by Faltings.
Upon comparing these two conjectures with the notion of B∗-admissible representations above, it is seen that if X is a proper smooth scheme over K (with good reduction) and V is the p-adic Galois representation obtained as is its ith p-adic étale cohomology group, then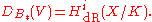
In other words, the Dieudonné modules should be thought of as giving the other cohomologies related to V.
In the late eighties, Fontaine and Uwe Jannsen formulated another comparison isomorphism conjecture, Cst, this time allowing X to have semi-stable reduction. Fontaine constructed a ring Bst with GK-action, a "Frobenius" φ, a filtration after extending scalars from K0 to K (and fixing an extension of the p-adic logarithm), and a "monodromy operator" N. When X has semi-stable reduction, the de Rham cohomology can be equipped with the φ-action and a monodromy operator by its comparison with the log-crystalline cohomology first introduced by Osamu Hyodo. The conjecture then states that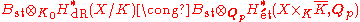
as vector spaces with φ-action, GK-action, filtration after extending scalars to K, and monodromy operator N. This conjecture was proved in the late nineties by Takeshi Tsuji.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, p-adic Hodge theory is a theory that provides a way to classify and study p-adic Galois representations of characteristic 0
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s with residual characteristic p (such as Qp
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
). The theory has its beginnings in Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
and John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
's study of Tate module
Tate module
In mathematics, a Tate module of an abelian group, named for John Tate, is a module constructed from an abelian group A. Often, this construction is made in the following situation: G is a commutative group scheme over a field K, Ks is the separable closure of K, and A = G...
s of abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
and the notion of Hodge–Tate representation. Hodge–Tate representations are related to certain decompositions of p-adic cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
theories analogous to the Hodge decomposition, hence the name p-adic Hodge theory. Further developments were inspired by properties of p-adic Galois representations arising from the étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
of varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. Jean-Marc Fontaine introduced many of the basic concepts of the field.
General classification of
p-adic representations Let K be a local field of residue field k of characteristic p. In this article, a p-adic representation of K (or of GK, the absolute Galois groupAbsolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of K) will be a continuous representation ρ : GK→ GL(V) where V is a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over Qp. The collection of all p-adic representations of K form an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
denoted
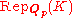in this article. p-adic Hodge theory provides subcollections of p-adic representations based on how nice they are, and also provides faithful functors to categories of linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
ic objects that are easier to study. The basic classification is as follows:
- Repcris(
where each collection is a full subcategory properly contained in the next. In order, these are the categories of cristalline representations, semistable representations, de Rham representations, Hodge–Tate representations, and all p-adic representations. In addition, two other categories of representations can be introduced, the potentially cristalline representations Reppcris(K) and the potentially semistable representations Reppst(K). The latter strictly contains the former which in turn generally strictly contains Repcris(K); additionally, Reppst(K) generally strictly contains Repst(K), and is contained in RepdR(K) (with equality when the residue field of K is finite, a statement called the p-adic monodromy theorem).
Period rings and comparison isomorphisms in arithmetic geometry
The general strategy of p-adic Hodge theory, introduced by Fontaine, is to construct certain so-called period rings such as BdR, Bst, Bcris, and BHT which have both an actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by GK and some linear algebraic structure and to consider so-called Dieudonné modules
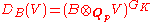
(where B is a period ring, and V is a p-adic representation) which no longer have a GK-action, but are endowed with linear algebraic structures inherited from the ring B. In particular, they are vector spaces over the fixed field
. This construction fits into the formalism of B-admissible representationsB-admissible representation
In mathematics, the formalism of B-admissible representations provides constructions of full Tannakian subcategories of the category of representations of a group G on finite-dimensional vector spaces over a given field E. In this theory, B is chosen to be a so-called -regular ring, i.e...
introduced by Fontaine. For a period ring like the aforementioned ones B∗ (for ∗ = HT, dR, st, cris), the category of p-adic representations Rep∗(K) mentioned above is the category of B∗-admissible
B-admissible representation
In mathematics, the formalism of B-admissible representations provides constructions of full Tannakian subcategories of the category of representations of a group G on finite-dimensional vector spaces over a given field E. In this theory, B is chosen to be a so-called -regular ring, i.e...
ones, i.e. those p-adic representations V for which
or, equivalently, the comparison morphism
B-admissible representation
In mathematics, the formalism of B-admissible representations provides constructions of full Tannakian subcategories of the category of representations of a group G on finite-dimensional vector spaces over a given field E. In this theory, B is chosen to be a so-called -regular ring, i.e...
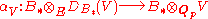
is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
This formalism (and the name period ring) grew out of a few results and conjectures regarding comparison isomorphisms in arithmetic and complex geometry
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
:
- If X is a proper smooth schemeScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
over CComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, there is a classical comparison isomorphism between the algebraic de Rham cohomology of X over C and the singular cohomology of X(C)
-
- This isomorphism can be obtained by considering a pairingPairingThe concept of pairing treated here occurs in mathematics.-Definition:Let R be a commutative ring with unity, and let M, N and L be three R-modules.A pairing is any R-bilinear map e:M \times N \to L...
obtained by integratingIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s in the algebraic de Rham cohomology over cyclesAlgebraic cycleIn mathematics, an algebraic cycle on an algebraic variety V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology of V that is directly accessible in algebraic geometry...
in the singular cohomology. The result of such an integration is called a period and is generally a complex number. This explains why the singular cohomology must be tensoredExtension of scalarsIn abstract algebra, extension of scalars is a means of producing a module over a ring S from a module over another ring R, given a homomorphism f : R \to S between them...
to C, and from this point of view, C can be said to contain all the periods necessary to compare algebraic de Rham cohomology with singular cohomology, and could hence be called a period ring in this situation.- In the mid sixties, Tate conjectured that a similar isomorphism should hold for proper smooth schemes X over K between algebraic de Rham cohomology and p-adic étale cohomology (the Hodge–Tate conjecture, also called CHT). Specifically, let CK be the completion of an algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K, let CK(i) denote CK where the action of GK is via g·z = χ(g)ig·z (where χ is the p-adic cyclotomic characterCyclotomic characterIn number theory, a cyclotomic character is a character of a Galois group giving the Galois action on a group of roots of unity. As a one-dimensional representation over a ring R, its representation space is generally denoted by R .-p-adic cyclotomic character:If p is a prime, and G is the absolute...
, and i is an integer), and let
. Then there is a functorial isomorphism
- In the mid sixties, Tate conjectured that a similar isomorphism should hold for proper smooth schemes X over K between algebraic de Rham cohomology and p-adic étale cohomology (the Hodge–Tate conjecture, also called CHT). Specifically, let CK be the completion of an algebraic closure
- of graded vector spaceGraded vector spaceIn mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
s with GK-action (the de Rham cohomology is equipped with the Hodge filtration, and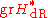
is its associated graded). This conjecture was proved by Gerd FaltingsGerd FaltingsGerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
in the late eighties after partial results by several other mathematicians (including Tate himself).- By combining the comparison of crystalline cohomologyCrystalline cohomologyIn mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
of an X over K which has good reduction with both algebraic de Rham cohomology and p-adic étale cohomology, a comparison isomorphism is obtained between algebraic de Rham cohomology and p-adic étale cohomology. Alexander GrothendieckAlexander GrothendieckAlexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
conjectured that there should be a way to go directly from algebraic de Rham cohomology to p-adic étale cohomology without going through crystalline cohomology. He termed this suggested relation the mysterious functor.
- By combining the comparison of crystalline cohomology
To improve the Hodge–Tate conjecture to one involving the de Rham cohomology (not just its associated graded), Fontaine constructed a filtered ring BdR whose associated graded is BHT and conjectured the following (called CdR) for any smooth proper scheme X over K
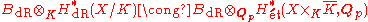
as filtered vector spaces with GK-action. In this way, BdR could be said to contain all (p-adic) periods required to compare algebraic de Rham cohomology with p-adic étale cohomology, just as the complex numbers above were used with the comparison with singular cohomology. This is where BdR obtains its name of ring of p-adic periods.
Similarly, to formulate a conjecture explaining Grothendieck's mysterious functor, Fontaine introduced a ring Bcris with GK-action, a "Frobenius" φ, and a filtration after extending scalars from K0 to K. He conjectured the following (called Ccris) for any smooth proper scheme X over K with good reduction
as vector spaces with φ-action, GK-action, and filtration after extending scalars to K (here
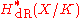is given its structure as a K0-vector space with φ-action given by its comparison with crystalline cohomology). Both the CdR and the Ccris conjectures were proved by Faltings.Upon comparing these two conjectures with the notion of B∗-admissible representations above, it is seen that if X is a proper smooth scheme over K (with good reduction) and V is the p-adic Galois representation obtained as is its ith p-adic étale cohomology group, then
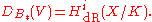
In other words, the Dieudonné modules should be thought of as giving the other cohomologies related to V.
In the late eighties, Fontaine and Uwe Jannsen formulated another comparison isomorphism conjecture, Cst, this time allowing X to have semi-stable reduction. Fontaine constructed a ring Bst with GK-action, a "Frobenius" φ, a filtration after extending scalars from K0 to K (and fixing an extension of the p-adic logarithm), and a "monodromy operator" N. When X has semi-stable reduction, the de Rham cohomology can be equipped with the φ-action and a monodromy operator by its comparison with the log-crystalline cohomology first introduced by Osamu Hyodo. The conjecture then states that
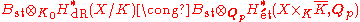
as vector spaces with φ-action, GK-action, filtration after extending scalars to K, and monodromy operator N. This conjecture was proved in the late nineties by Takeshi Tsuji.