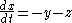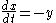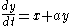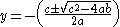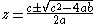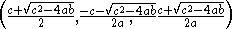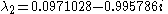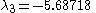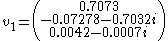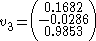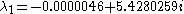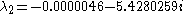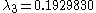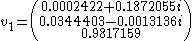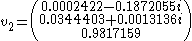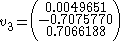Rössler attractor
Encyclopedia


Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
for the Rössler system, a system of three non-linear ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s. These differential equations define a continuous-time dynamical system that exhibits chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
dynamics associated with the fractal properties of the attractor. Some properties of the Rössler system can be deduced via linear methods such as eigenvectors, but the main features of the system require non-linear methods such as Poincaré map
Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
s and bifurcation diagram
Bifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values of a system as a function of a bifurcation parameter in the system...
s. The original Rössler paper says the Rössler attractor was intended to behave similarly to the Lorenz attractor
Lorenz attractor
The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
, but also be easier to analyze qualitatively. An orbit within the attractor follows an outward spiral close to the
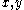 plane around an unstable fixed point. Once the graph spirals out enough, a second fixed point influences the graph, causing a rise and twist in the
plane around an unstable fixed point. Once the graph spirals out enough, a second fixed point influences the graph, causing a rise and twist in the  -dimension. In the time domain, it becomes apparent that although each variable is oscillating within a fixed range of values, the oscillations are chaotic. This attractor has some similarities to the Lorenz attractor, but is simpler and has only one manifold
-dimension. In the time domain, it becomes apparent that although each variable is oscillating within a fixed range of values, the oscillations are chaotic. This attractor has some similarities to the Lorenz attractor, but is simpler and has only one manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. Otto Rössler
Otto Rössler
Otto E. Rössler is a German biochemist and is notable for his work on chaos theory and his theoretical equation known as the Rössler attractor.-Biography:...
designed the Rössler attractor in 1976, but the originally theoretical equations were later found to be useful in modeling equilibrium in chemical reactions. The defining equations are:
Rössler studied the chaotic attractor with
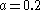 ,
, 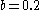 , and
, and 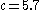 , though properties of
, though properties of 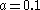 ,
, 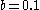 , and
, and 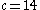 have been more commonly used since.
have been more commonly used since.An analysis
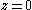 , allows examination of the behavior on the
, allows examination of the behavior on the 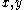 plane
planeThe stability in the
 plane can then be found by calculating the eigenvalues of the Jacobian
plane can then be found by calculating the eigenvalues of the JacobianJacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
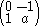 , which are
, which are 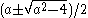 . From this, we can see that when
. From this, we can see that when 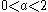 , the eigenvalues are complex and both have a positive real component, making the origin unstable with an outwards spiral on the
, the eigenvalues are complex and both have a positive real component, making the origin unstable with an outwards spiral on the 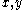 plane. Now consider the
plane. Now consider the  plane behavior within the context of this range for
plane behavior within the context of this range for  . So long as
. So long as  is smaller than
is smaller than  , the
, the  term will keep the orbit close to the
term will keep the orbit close to the 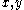 plane. As the orbit approaches
plane. As the orbit approaches  greater than
greater than  , the
, the  -values begin to climb. As
-values begin to climb. As  climbs, though, the
climbs, though, the  in the equation for
in the equation for 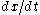 stops the growth in
stops the growth in  .
.Fixed points
In order to find the fixed points, the three Rössler equations are set to zero and the ( ,
,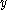 ,
, ) coordinates of each fixed point were determined by solving the resulting equations. This yields the general equations of each of the fixed point coordinates:
) coordinates of each fixed point were determined by solving the resulting equations. This yields the general equations of each of the fixed point coordinates:
Which in turn can be used to show the actual fixed points for a given set of parameter values:
As shown in the general plots of the Rössler Attractor above, one of these fixed points resides in the center of the attractor loop and the other lies comparatively removed from the attractor.
Eigenvalues and eigenvectors
The stability of each of these fixed points can be analyzed by determining their respective eigenvalues and eigenvectors. Beginning with the Jacobian: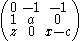
the eigenvalues can be determined by solving the following cubic:
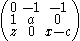
For the centrally located fixed point, Rössler’s original parameter values of a=0.2, b=0.2, and c=5.7 yield eigenvalues of:
(Using Mathematica 7)
The magnitude of a negative eigenvalue characterizes the level of attraction along the corresponding eigenvector. Similarly the magnitude of a positive eigenvalue characterizes the level of repulsion along the corresponding eigenvector.
The eigenvectors corresponding to these eigenvalues are:
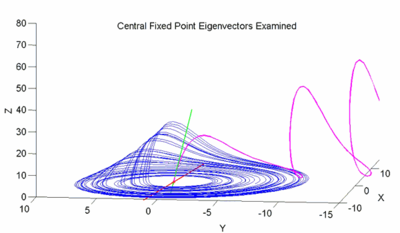
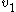 and
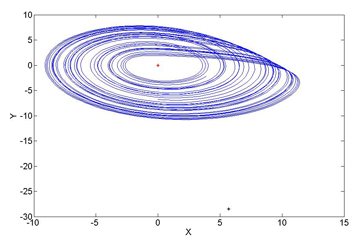
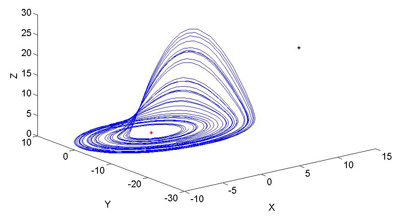
and 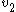 ) are responsible for the steady outward slide that occurs in the main disk of the attractor. The last eigenvalue/eigenvector pair is attracting along an axis that runs through the center of the manifold and accounts for the z motion that occurs within the attractor. This effect is roughly demonstrated with the figure below.
) are responsible for the steady outward slide that occurs in the main disk of the attractor. The last eigenvalue/eigenvector pair is attracting along an axis that runs through the center of the manifold and accounts for the z motion that occurs within the attractor. This effect is roughly demonstrated with the figure below.The figure examines the central fixed point eigenvectors. The blue line corresponds to the standard Rössler attractor generated with
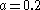 ,
, 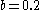 , and
, and 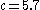 . The red dot in the center of this attractor is
. The red dot in the center of this attractor is 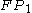 . The red line intersecting that fixed point is an illustration of the repulsing plane generated by
. The red line intersecting that fixed point is an illustration of the repulsing plane generated by 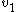 and
and 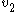 . The green line is an illustration of the attracting
. The green line is an illustration of the attracting 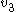 . The magenta line is generated by stepping backwards through time from a point on the attracting eigenvector which is slightly above
. The magenta line is generated by stepping backwards through time from a point on the attracting eigenvector which is slightly above 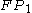 – it illustrates the behavior of points that become completely dominated by that vector. Note that the magenta line nearly touches the plane of the attractor before being pulled upwards into the fixed point; this suggests that the general appearance and behavior of the Rössler attractor is largely a product of the interaction between the attracting
– it illustrates the behavior of points that become completely dominated by that vector. Note that the magenta line nearly touches the plane of the attractor before being pulled upwards into the fixed point; this suggests that the general appearance and behavior of the Rössler attractor is largely a product of the interaction between the attracting  and the repelling
and the repelling  and
and 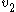 plane. Specifically it implies that a sequence generated from the Rössler equations will begin to loop around
plane. Specifically it implies that a sequence generated from the Rössler equations will begin to loop around 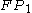 , start being pulled upwards into the
, start being pulled upwards into the 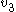 vector, creating the upward arm of a curve that bends slightly inward toward the vector before being pushed outward again as it is pulled back towards the repelling plane.
vector, creating the upward arm of a curve that bends slightly inward toward the vector before being pushed outward again as it is pulled back towards the repelling plane.For the outlier fixed point, Rössler’s original parameter values of
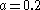 ,
, 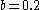 , and
, and  yield eigenvalues of:
yield eigenvalues of:
The eigenvectors corresponding to these eigenvalues are:
Although these eigenvalues and eigenvectors exist in the Rössler attractor, their influence is confined to iterations of the Rössler system whose initial conditions are in the general vicinity of this outlier fixed point. Except in those cases where the initial conditions lie on the attracting plane generated by
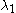 and
and 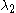 , this influence effectively involves pushing the resulting system towards the general Rössler attractor. As the resulting sequence approaches the central fixed point and the attractor itself, the influence of this distant fixed point (and its eigenvectors) will wane.
, this influence effectively involves pushing the resulting system towards the general Rössler attractor. As the resulting sequence approaches the central fixed point and the attractor itself, the influence of this distant fixed point (and its eigenvectors) will wane.Poincaré map
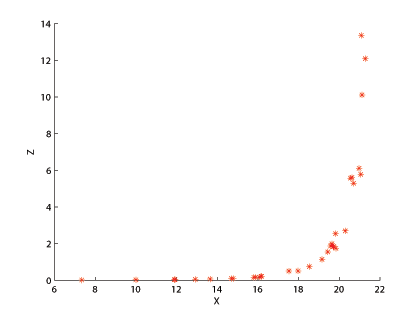
Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
is constructed by plotting the value of the function every time it passes through a set plane in a specific direction. An example would be plotting the
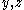 value every time it passes through the
value every time it passes through the  plane where
plane where  is changing from negative to positive, commonly done when studying the Lorenz attractor. In the case of the Rössler attractor, the
is changing from negative to positive, commonly done when studying the Lorenz attractor. In the case of the Rössler attractor, the 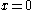 plane is uninteresting, as the map always crosses the
plane is uninteresting, as the map always crosses the 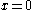 plane at
plane at 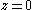 due to the nature of the Rössler equations. In the
due to the nature of the Rössler equations. In the 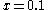 plane for
plane for  ,
, 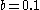 ,
, 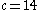 , the Poincaré map shows the upswing in
, the Poincaré map shows the upswing in  values as
values as  increases, as is to be expected due to the upswing and twist section of the Rössler plot. The number of points in this specific Poincaré plot is infinite, but when a different
increases, as is to be expected due to the upswing and twist section of the Rössler plot. The number of points in this specific Poincaré plot is infinite, but when a different  value is used, the number of points can vary. For example, with a
value is used, the number of points can vary. For example, with a  value of 4, there is only one point on the Poincaré map, because the function yields a periodic orbit of period one, or if the
value of 4, there is only one point on the Poincaré map, because the function yields a periodic orbit of period one, or if the  value is set to 12.8, there would be six points corresponding to a period six orbit.
value is set to 12.8, there would be six points corresponding to a period six orbit.Mapping local maxima

 against the immediately preceding local maxima. When visualized, the plot resembled the tent map, implying that similar analysis can be used between the map and attractor. For the Rössler attractor, when the
against the immediately preceding local maxima. When visualized, the plot resembled the tent map, implying that similar analysis can be used between the map and attractor. For the Rössler attractor, when the 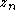 local maximum is plotted against the next local
local maximum is plotted against the next local  maximum,
maximum,  , the resulting plot
, the resulting plot(shown here for
 ,
, 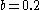 ,
, 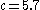 ) is unimodal, resembling a skewed Henon map. Knowing that the Rössler attractor can be used to create a pseudo 1-d map, it then follows to use similar analysis methods. The bifurcation diagram is specifically a useful analysis method.
) is unimodal, resembling a skewed Henon map. Knowing that the Rössler attractor can be used to create a pseudo 1-d map, it then follows to use similar analysis methods. The bifurcation diagram is specifically a useful analysis method.Variation of parameters
Rössler attractor's behavior is largely a factor of the values of its constant parameters ,
,  , and
, and  . In general, varying each parameter has a comparable effect by causing the system to converge toward a periodic orbit, fixed point, or escape towards infinity, however the specific ranges and behaviors induced vary substantially for each parameter. Periodic orbits, or "unit cycles," of the Rössler system are defined by the number of loops around the central point that occur before the loops series begins to repeat itself.
. In general, varying each parameter has a comparable effect by causing the system to converge toward a periodic orbit, fixed point, or escape towards infinity, however the specific ranges and behaviors induced vary substantially for each parameter. Periodic orbits, or "unit cycles," of the Rössler system are defined by the number of loops around the central point that occur before the loops series begins to repeat itself.Bifurcation diagram
Bifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values of a system as a function of a bifurcation parameter in the system...
s are a common tool for analyzing the behavior of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, of which the Rössler attractor is one. They are created by running the equations of the system, holding all but one of the variables constant and varying the last one. Then, a graph.is plotted of the points that a particular value for the changed variable visits after transient factors have been neutralised. Chaotic regions are indicated by filled-in regions of the plot.
Varying a
Here,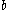 is fixed at 0.2,
is fixed at 0.2,  is fixed at 5.7 and
is fixed at 5.7 and  changes. Numerical examination of the attractor's behavior over changing
changes. Numerical examination of the attractor's behavior over changing  suggests it has a disproportional influence over the attractor's behavior. The results of the analysis are:
suggests it has a disproportional influence over the attractor's behavior. The results of the analysis are:
-
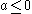 : Converges to the centrally located fixed point
: Converges to the centrally located fixed point -
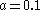 : Unit cycle of period 1
: Unit cycle of period 1 -
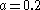 : Standard parameter value selected by Rössler, chaotic
: Standard parameter value selected by Rössler, chaotic -
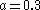 : Chaotic attractor, significantly more Möbius stripMöbius stripThe Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
: Chaotic attractor, significantly more Möbius stripMöbius stripThe Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
-like (folding over itself). -
 : Similar to .3, but increasingly chaotic
: Similar to .3, but increasingly chaotic -
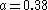 : Similar to .35, but increasingly chaotic.
: Similar to .35, but increasingly chaotic.
Varying b
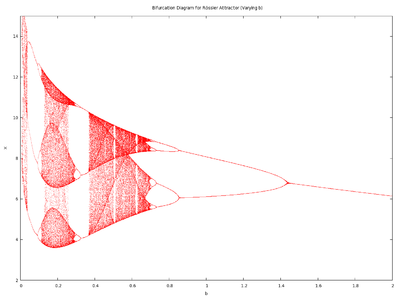
 is fixed at 0.2,
is fixed at 0.2,  is fixed at 5.7 and
is fixed at 5.7 and 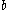 changes. As shown in the accompanying diagram, as
changes. As shown in the accompanying diagram, as 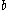 approaches 0 the attractor approaches infinity (note the upswing for very small values of
approaches 0 the attractor approaches infinity (note the upswing for very small values of 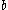 . Comparative to the other parameters, varying
. Comparative to the other parameters, varying 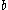 generates a greater range when period-3 and period-6 orbits will occur. In contrast to
generates a greater range when period-3 and period-6 orbits will occur. In contrast to  and
and  , higher values of
, higher values of 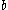 converge to period-1, not to a chaotic state.
converge to period-1, not to a chaotic state.Varying c
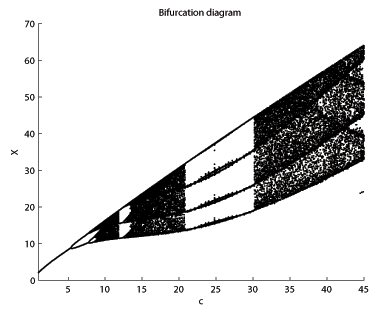
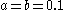 and
and  changes. The bifurcation diagram
changes. The bifurcation diagramBifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values of a system as a function of a bifurcation parameter in the system...
reveals that low values of
 are periodic, but quickly become chaotic as
are periodic, but quickly become chaotic as  increases. This pattern repeats itself as
increases. This pattern repeats itself as  increases – there are sections of periodicity interspersed with periods of chaos, and the trend is towards higher-period orbits as
increases – there are sections of periodicity interspersed with periods of chaos, and the trend is towards higher-period orbits as  increases. For example, the period one orbit only appears for values of
increases. For example, the period one orbit only appears for values of  around 4 and is never found again in the bifurcation diagram. The same phenomenon is seen with period three; until
around 4 and is never found again in the bifurcation diagram. The same phenomenon is seen with period three; until 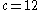 , period three orbits can be found, but thereafter, they do not appear.
, period three orbits can be found, but thereafter, they do not appear.A graphical illustration of the changing attractor over a range of
 values illustrates the general behavior seen for all of these parameter analyses – the frequent transitions between periodicity and aperiodicity.
values illustrates the general behavior seen for all of these parameter analyses – the frequent transitions between periodicity and aperiodicity.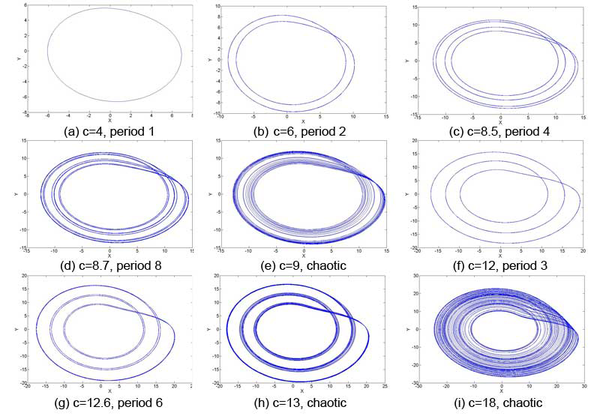
 is varied over a range of values. These images were generated with
is varied over a range of values. These images were generated with 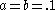 .
.
 , period-1 orbit.
, period-1 orbit.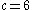 , period-2 orbit.
, period-2 orbit.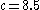 , period-4 orbit.
, period-4 orbit.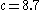 , period-8 orbit.
, period-8 orbit.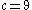 , sparse chaotic attractor.
, sparse chaotic attractor.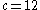 , period-3 orbit.
, period-3 orbit.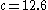 , period-6 orbit.
, period-6 orbit.-
 , sparse chaotic attractor.
, sparse chaotic attractor. 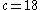 , filled-in chaotic attractor.
, filled-in chaotic attractor.
Links to other topics
The banding evident in the Rössler attractor is similar to a Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
rotated about its midpoint. Additionally, the half-twist in the Rössler attractor makes it similar to a Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
.
See also
- Lorenz attractorLorenz attractorThe Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
- List of chaotic maps
- Chaos theoryChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
- Dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
- Fractals
- Otto RösslerOtto RösslerOtto E. Rössler is a German biochemist and is notable for his work on chaos theory and his theoretical equation known as the Rössler attractor.-Biography:...