
Limit set
Encyclopedia
In mathematics
, especially in the study of dynamical system
s, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time. Limit sets are important because they can be used to understand the long term behavior of a dynamical system.
In general limits sets can be very complicated as in the case of strange attractors, but for 2-dimensional dynamical systems the Poincaré–Bendixson theorem
provides a simple characterization of all possible limit sets as a union of fixed points and periodic orbits.
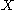 be a metric space
be a metric space
, and let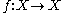 be a continuous function
be a continuous function
. The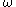 -limit set of
-limit set of 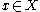 , denoted by
, denoted by 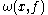 , is the set of cluster points of the forward orbit
, is the set of cluster points of the forward orbit 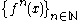 of the iterated function
of the iterated function
 . Hence,
. Hence, 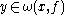 if and only if
if and only if
there is a strictly increasing sequence of natural numbers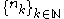 such that
such that 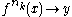 as
as 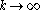 . Another way to express this is
. Another way to express this is
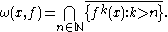
The points in the limit set are non-wandering (but may not be recurrent point
s).
If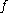 is a homeomorphism
is a homeomorphism
(that is, a bicontinuous bijection), then the -limit set is defined in a similar fashion, but for the backward orbit; i.e.
-limit set is defined in a similar fashion, but for the backward orbit; i.e. 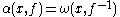 .
.
Both sets are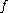 -invariant, and if
-invariant, and if 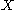 is compact
is compact
, they are compact and nonempty.
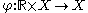 , a point x and an orbit
, a point x and an orbit
γ through x, we call a point y an ω-limit point of γ if there exists a sequence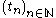 in R so that
in R so that
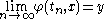 .
.
Analogously we call y an α-limit point if there exists a sequence in R so that
in R so that
 .
.
The set of all ω-limit points (α-limit points) for a given orbit γ is called ω-limit set (α-limit set) for γ and denoted limω γ (limα γ).
If the ω-limit set (α-limit set) is disjunct from the orbit γ, that is limω γ ∩ γ = ∅ (limα γ ∩ γ = ∅) , we call limω γ (limα γ) a ω-limit cycle (α-limit cycle).
Alternatively the limit sets can be defined as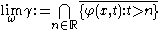
and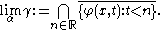
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the study of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time. Limit sets are important because they can be used to understand the long term behavior of a dynamical system.
Types
- fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s - periodic orbits
- limit cycles
- attractorAttractorAn attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
s.
In general limits sets can be very complicated as in the case of strange attractors, but for 2-dimensional dynamical systems the Poincaré–Bendixson theorem
Poincaré–Bendixson theorem
In mathematics, the Poincaré–Bendixson theorem is a statement about the long-term behaviour of orbits of continuous dynamical systems on the plane.-Theorem:...
provides a simple characterization of all possible limit sets as a union of fixed points and periodic orbits.
Definition for iterated functions
Let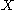 be a metric space
be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, and let
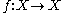 be a continuous function
be a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. The
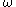 -limit set of
-limit set of 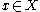 , denoted by
, denoted by 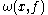 , is the set of cluster points of the forward orbit
, is the set of cluster points of the forward orbit 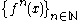 of the iterated function
of the iterated functionIterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
 . Hence,
. Hence, 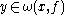 if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there is a strictly increasing sequence of natural numbers
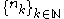 such that
such that 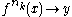 as
as 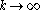 . Another way to express this is
. Another way to express this is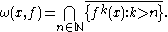
The points in the limit set are non-wandering (but may not be recurrent point
Recurrent point
In mathematics, a recurrent point for function f is a point that is in the limit set of the iterated function f. Any neighborhood containing the recurrent point will also contain iterates of it as well.-Definition:...
s).
If
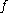 is a homeomorphism
is a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
(that is, a bicontinuous bijection), then the
 -limit set is defined in a similar fashion, but for the backward orbit; i.e.
-limit set is defined in a similar fashion, but for the backward orbit; i.e. 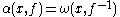 .
.Both sets are
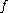 -invariant, and if
-invariant, and if 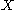 is compact
is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, they are compact and nonempty.
Definition for flows
Given a real dynamical system (T, X, φ) with flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
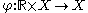 , a point x and an orbit
, a point x and an orbitOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
γ through x, we call a point y an ω-limit point of γ if there exists a sequence
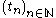 in R so that
in R so that
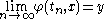 .
.Analogously we call y an α-limit point if there exists a sequence
 in R so that
in R so that
 .
.The set of all ω-limit points (α-limit points) for a given orbit γ is called ω-limit set (α-limit set) for γ and denoted limω γ (limα γ).
If the ω-limit set (α-limit set) is disjunct from the orbit γ, that is limω γ ∩ γ = ∅ (limα γ ∩ γ = ∅) , we call limω γ (limα γ) a ω-limit cycle (α-limit cycle).
Alternatively the limit sets can be defined as
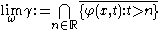
and
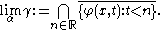
Examples
- For any periodic orbit γ of a dynamical system, limω γ = limα γ = γ
- For any fixed pointFixed point"Fixed point" has many meanings in science, most of them mathematical.* Fixed point * Fixed-point combinator* Fixed-point arithmetic, a manner of doing arithmetic on computers* Benchmark , fixed points used by geodesists...
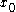 of a dynamical system, limω
of a dynamical system, limω 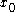 = limα
= limα 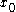 =
= 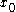
Properties
- limω γ and limα γ are closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
- if X is compact then limω γ and limα γ are nonempty, compact and connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
- limω γ and limα γ are φ-invariant, that is φ(R × limω γ) = limω γ and φ(R × limα γ) = limα γ
See also
- Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
- Stable setStable manifoldIn mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
- Limit cycle
- Periodic pointPeriodic pointIn mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
- Non-wandering set
- Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...

