
Stable manifold
Encyclopedia
In mathematics
, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor
or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set
.
or has discrete-time dynamics. Similar notions apply for systems whose time evolution is given by a flow
.
Let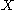 be a topological space
be a topological space
, and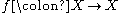 a homeomorphism
a homeomorphism
. If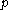 is a fixed point
is a fixed point
for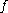 , the stable set of
, the stable set of 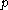 is defined by
is defined by
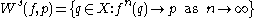
and the unstable set of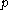 is defined by
is defined by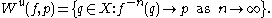
Here,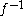 denotes the inverse
denotes the inverse
of the function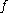 , i.e.
, i.e.
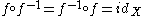 , where
, where 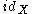 is the identity map on
is the identity map on 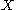 .
.
If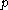 is a periodic point
is a periodic point
of least period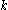 , then it is a fixed point of
, then it is a fixed point of 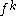 , and the stable and unstable sets of
, and the stable and unstable sets of 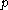 are
are
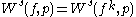
and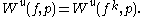
Given a neighborhood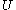 of
of 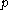 , the local stable and unstable sets of
, the local stable and unstable sets of 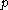 are defined by
are defined by
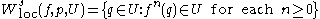
and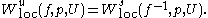
If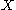 is metrizable, we can define the stable and unstable sets for any point by
is metrizable, we can define the stable and unstable sets for any point by
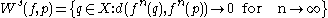
and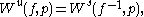
where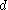 is a metric
is a metric
for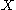 . This definition clearly coincides with the previous one when
. This definition clearly coincides with the previous one when 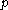 is a periodic point.
is a periodic point.
Suppose now that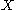 is a compact
is a compact
smooth manifold, and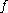 is a
is a 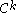 diffeomorphism
diffeomorphism
,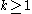 . If
. If 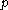 is a hyperbolic periodic point, the stable manifold theorem
is a hyperbolic periodic point, the stable manifold theorem
assures that for some neighborhood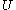 of
of 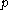 , the local stable and unstable sets are
, the local stable and unstable sets are 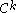 embedded disks, whose tangent space
embedded disks, whose tangent space
s at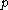 are
are 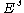 and
and 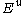 (the stable and unstable spaces of
(the stable and unstable spaces of 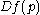 ), respectively; moreover, they vary continuously (in a certain sense) in a neighborhood of
), respectively; moreover, they vary continuously (in a certain sense) in a neighborhood of 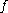 in the
in the 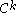 topology of
topology of 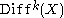 (the space of all
(the space of all 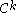 diffeomorphisms from
diffeomorphisms from 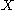 to itself). Finally, the stable and unstable sets are
to itself). Finally, the stable and unstable sets are 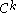 injectively immersed disks. This is why they are commonly called stable and unstable manifolds. This result is also valid for nonperiodic points, as long as they lie in some hyperbolic set
injectively immersed disks. This is why they are commonly called stable and unstable manifolds. This result is also valid for nonperiodic points, as long as they lie in some hyperbolic set
(stable manifold theorem for hyperbolic sets).
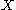 is a (finite dimensional) vector space and
is a (finite dimensional) vector space and 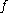 an isomorphism, its stable and unstable sets are called stable space and unstable space, respectively.
an isomorphism, its stable and unstable sets are called stable space and unstable space, respectively.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set
Hyperbolic set
In dynamical systems theory, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle may be split into two invariant subbundles, one of which is contracting and the other is expanding under f, with respect to some...
.
Definition
The following provides a definition for the case of a system that is either an iterated functionIterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
or has discrete-time dynamics. Similar notions apply for systems whose time evolution is given by a flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
.
Let
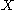 be a topological space
be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, and
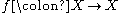 a homeomorphism
a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. If
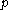 is a fixed point
is a fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
for
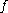 , the stable set of
, the stable set of 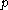 is defined by
is defined by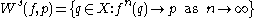
and the unstable set of
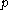 is defined by
is defined by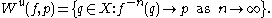
Here,
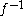 denotes the inverse
denotes the inverseInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of the function
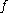 , i.e.
, i.e.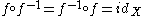 , where
, where 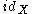 is the identity map on
is the identity map on 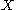 .
.If
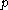 is a periodic point
is a periodic pointPeriodic point
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
of least period
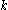 , then it is a fixed point of
, then it is a fixed point of 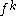 , and the stable and unstable sets of
, and the stable and unstable sets of 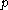 are
are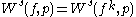
and
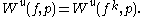
Given a neighborhood
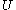 of
of 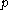 , the local stable and unstable sets of
, the local stable and unstable sets of 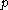 are defined by
are defined by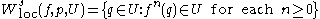
and
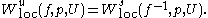
If
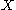 is metrizable, we can define the stable and unstable sets for any point by
is metrizable, we can define the stable and unstable sets for any point by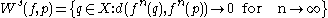
and
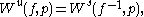
where
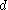 is a metric
is a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
for
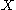 . This definition clearly coincides with the previous one when
. This definition clearly coincides with the previous one when 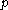 is a periodic point.
is a periodic point.Suppose now that
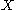 is a compact
is a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
smooth manifold, and
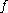 is a
is a 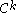 diffeomorphism
diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
,
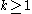 . If
. If 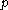 is a hyperbolic periodic point, the stable manifold theorem
is a hyperbolic periodic point, the stable manifold theoremStable manifold theorem
In mathematics, especially in the study of dynamical systems and differential equations, the stable manifold theorem is an important result about the structure of the set of orbits approaching a given hyperbolic fixed point.- Stable manifold theorem :...
assures that for some neighborhood
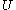 of
of 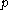 , the local stable and unstable sets are
, the local stable and unstable sets are 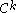 embedded disks, whose tangent space
embedded disks, whose tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s at
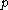 are
are 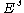 and
and 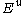 (the stable and unstable spaces of
(the stable and unstable spaces of 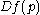 ), respectively; moreover, they vary continuously (in a certain sense) in a neighborhood of
), respectively; moreover, they vary continuously (in a certain sense) in a neighborhood of 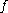 in the
in the 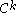 topology of
topology of 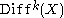 (the space of all
(the space of all 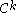 diffeomorphisms from
diffeomorphisms from 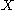 to itself). Finally, the stable and unstable sets are
to itself). Finally, the stable and unstable sets are 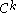 injectively immersed disks. This is why they are commonly called stable and unstable manifolds. This result is also valid for nonperiodic points, as long as they lie in some hyperbolic set
injectively immersed disks. This is why they are commonly called stable and unstable manifolds. This result is also valid for nonperiodic points, as long as they lie in some hyperbolic setHyperbolic set
In dynamical systems theory, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle may be split into two invariant subbundles, one of which is contracting and the other is expanding under f, with respect to some...
(stable manifold theorem for hyperbolic sets).
Remark
If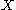 is a (finite dimensional) vector space and
is a (finite dimensional) vector space and 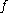 an isomorphism, its stable and unstable sets are called stable space and unstable space, respectively.
an isomorphism, its stable and unstable sets are called stable space and unstable space, respectively.

