
Topological algebra
Encyclopedia
In mathematics
, a topological algebra A over a topological field K is a topological vector space
together with a continuous multiplication
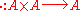

that makes it an algebra
over K. A unital associative
topological algebra is a topological ring
.
An example of a topological algebra is the algebra C[0,1] of continuous real-valued functions on the closed unit interval [0,1],
or more generally any Banach algebra
.
The term was coined by David van Dantzig
; it appears in the title of his doctoral dissertation
(1931).
The natural notion of subspace in a topological algebra is that of a (topologically) closed subalgebra
. A topological algebra A is said to be generated by a subset S if A itself is the smallest closed subalgebra of A that contains S. For example by the Stone–Weierstrass theorem, the set {id[0,1]} consisting only of the identity function id[0,1] is a generating set of the Banach algebra C[0,1].
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a topological algebra A over a topological field K is a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
together with a continuous multiplication
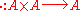

that makes it an algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over K. A unital associative
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
topological algebra is a topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
.
An example of a topological algebra is the algebra C[0,1] of continuous real-valued functions on the closed unit interval [0,1],
or more generally any Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
.
The term was coined by David van Dantzig
David van Dantzig
David van Dantzig was a Dutch mathematician, well known for the construction in topology of the dyadic solenoid....
; it appears in the title of his doctoral dissertation
Thesis
A dissertation or thesis is a document submitted in support of candidature for an academic degree or professional qualification presenting the author's research and findings...
(1931).
The natural notion of subspace in a topological algebra is that of a (topologically) closed subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
. A topological algebra A is said to be generated by a subset S if A itself is the smallest closed subalgebra of A that contains S. For example by the Stone–Weierstrass theorem, the set {id[0,1]} consisting only of the identity function id[0,1] is a generating set of the Banach algebra C[0,1].

