Gieseking manifold
Encyclopedia
In mathematics
, the Gieseking manifold, is a cusped hyperbolic
3-manifold
of finite volume. It is non-orientable
and has the smallest volume among non-compact hyperbolic manifolds, having volume approximately 1.01494161. It was discovered by .
The Gieseking manifold can be constructed by removing the vertices from a tetrahedron
, then gluing the faces together in pairs using affine-linear maps. Label the vertices 0, 1, 2, 3. Glue the face with vertices 0,1,2 to the face with vertices 3,1,0 in that order. Glue the face 0,2,3 to the face 3,2,1 in that order. In the hyperbolic structure of the Gieseking manifold, this ideal tetrahedron is the canonical polyhedral decomposition of Epstein-Penner. Moreover, the angle made by the faces is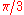
. The triangulation has one tetrahedron, two faces, one edge and no vertices, so all the edges of the original tetrahedron are glued together.
The Gieseking manifold has a double cover homeomorphic
to the figure eight knot complement
. The underlying compact manifold has boundary a Klein bottle
, and the first homology group of the Gieseking manifold is the integers.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Gieseking manifold, is a cusped hyperbolic
Hyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
of finite volume. It is non-orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
and has the smallest volume among non-compact hyperbolic manifolds, having volume approximately 1.01494161. It was discovered by .
The Gieseking manifold can be constructed by removing the vertices from a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, then gluing the faces together in pairs using affine-linear maps. Label the vertices 0, 1, 2, 3. Glue the face with vertices 0,1,2 to the face with vertices 3,1,0 in that order. Glue the face 0,2,3 to the face 3,2,1 in that order. In the hyperbolic structure of the Gieseking manifold, this ideal tetrahedron is the canonical polyhedral decomposition of Epstein-Penner. Moreover, the angle made by the faces is
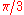. The triangulation has one tetrahedron, two faces, one edge and no vertices, so all the edges of the original tetrahedron are glued together.The Gieseking manifold has a double cover homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the figure eight knot complement
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
. The underlying compact manifold has boundary a Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, and the first homology group of the Gieseking manifold is the integers.