
Sphere theorem (3-manifolds)
Encyclopedia
In mathematics, in the topology
of 3-manifold
s, the sphere theorem of gives conditions for elements of the second homotopy group of a 3-manifold to be represented by embedded spheres.
One example is the following:
Let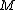 be an orientable 3-manifold such that
be an orientable 3-manifold such that 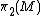 is not the trivial group. Then there exists a non-zero element of
is not the trivial group. Then there exists a non-zero element of
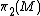 having a representative that is an embedding
having a representative that is an embedding
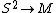 .
.
The proof of this version can be based on transversality
methods, see Batude below.
Another more general version (also called the projective plane theorem due to Epstein) is:
Let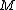 be any 3-manifold and
be any 3-manifold and 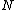 a
a 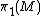 -invariant
-invariant
subgroup of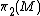 . If
. If 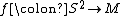 is a general position
is a general position
map such that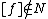 and
and 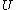 is any neighborhood of the singular set
is any neighborhood of the singular set 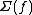 , then there is a map
, then there is a map 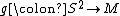 satisfying
satisfying
quoted in Hempel (p. 54)
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s, the sphere theorem of gives conditions for elements of the second homotopy group of a 3-manifold to be represented by embedded spheres.
One example is the following:
Let
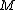 be an orientable 3-manifold such that
be an orientable 3-manifold such that 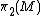 is not the trivial group. Then there exists a non-zero element of
is not the trivial group. Then there exists a non-zero element of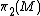 having a representative that is an embedding
having a representative that is an embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
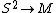 .
.The proof of this version can be based on transversality
Transversality theorem
In differential topology, the transversality theorem, also known as the Thom Transversality Theorem, is a major result that describes the transversal intersection properties of a smooth family of smooth maps...
methods, see Batude below.
Another more general version (also called the projective plane theorem due to Epstein) is:
Let
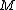 be any 3-manifold and
be any 3-manifold and 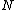 a
a 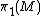 -invariant
-invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
subgroup of
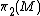 . If
. If 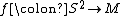 is a general position
is a general positionGeneral position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
map such that
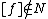 and
and 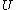 is any neighborhood of the singular set
is any neighborhood of the singular set 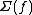 , then there is a map
, then there is a map 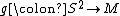 satisfying
satisfying ,
,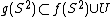 ,
,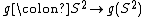 is a covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
is a covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
, and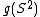 is a 2-sided2-sidedIn topology, a compact codimension one submanifold F of a manifold M is said to be 2-sided in M when there is an embeddingwith h=x for each x\in F andIn other words, if its normal bundle is trivial....
is a 2-sided2-sidedIn topology, a compact codimension one submanifold F of a manifold M is said to be 2-sided in M when there is an embeddingwith h=x for each x\in F andIn other words, if its normal bundle is trivial....
submanifold (2-sphere or projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
) of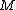 .
.
quoted in Hempel (p. 54)

