
I-bundle
Encyclopedia

In mathematics, an I-bundle is a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
whose fiber is an interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
and whose base is a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. Any kind of interval, open, closed, semi-open, semi-closed, open-bounded, compact, even rays, can be the fiber.
Two simple examples of I-bundles are the annulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
and the Möbius band
Mobius Band
Mobius Band is an electronic rock trio from Brooklyn, New York consisting of Noam Schatz , Peter Sax , and Ben Sterling .-History:...
, the only two possible I-bundles over the circle
 . The annulus is a trivial or untwisted bundle because it corresponds to the Cartesian product
. The annulus is a trivial or untwisted bundle because it corresponds to the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
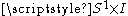 , and the Möbius band is a non-trivial or twisted bundle. Both bundles are 2-manifolds, but the annulus is an orientable manifold while the Möbius band is a non-orientable manifold.
, and the Möbius band is a non-trivial or twisted bundle. Both bundles are 2-manifolds, but the annulus is an orientable manifold while the Möbius band is a non-orientable manifold.Curiously, there are only two kinds of I-bundles when the base manifold is any surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
but the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
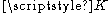 . That surface has three I-bundles: the trivial bundle
. That surface has three I-bundles: the trivial bundle 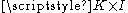 and two twisted bundles.
and two twisted bundles.Together with the Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s, I-bundles are fundamental elementary building blocks for the description of three dimensional spaces. These observations are simple well known facts on elementary 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s.
Line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s are both I-bundles and vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s of rank one.
When considering I-bundles, one is interested mostly in their topological properties and not their possible vector properties, as we might be for line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s.
External links
- Example of use of I-bundles, nice pdf-slide presentation by Jeff Boerner at Dept. of Math, University of Iowa.
- I-bundles over the Klein-Bottle, "elementary" work on the orientable I-bundle over K, by Maria Rita Casali, Dipartimento di Matematica Pura e Applicata, Università di Modena e Reggio Emilia.

