
Trigenus
Encyclopedia
In low-dimensional topology
, the trigenus of a closed
3-manifold
is an invariant consisting of an ordered triple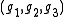 . It is obtained by minimizing the genera of three orientable handle bodies
. It is obtained by minimizing the genera of three orientable handle bodies
— with no intersection between their interiors— which decompose the manifold as far as the Heegaard
genus need only two.
That is, a decomposition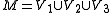 with
with
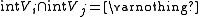
for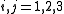 and being
and being 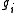 the genus of
the genus of 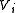 .
.
For orientable spaces,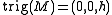 ,
,
where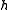 is
is 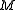 's Heegaard genus.
's Heegaard genus.
For non-orientable spaces the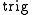 has the form
has the form 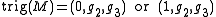
depending on the
image of the first Stiefel–Whitney characteristic class
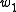 under a Bockstein homomorphism
under a Bockstein homomorphism
, respectively for
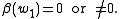
It has been proved that the number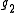 has a relation with the concept of Stiefel–Whitney surface, that is, an orientable surface
has a relation with the concept of Stiefel–Whitney surface, that is, an orientable surface 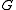 which is embedded in
which is embedded in 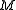 , has minimal genus and represents the first Stiefel–Whitney class under the duality map
, has minimal genus and represents the first Stiefel–Whitney class under the duality map 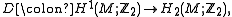 , that is,
, that is, 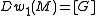 . If
. If 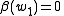 then
then 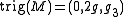 , and if
, and if 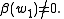
then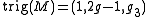 .
.
Low-dimensional topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...
, the trigenus of a closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
is an invariant consisting of an ordered triple
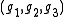 . It is obtained by minimizing the genera of three orientable handle bodies
. It is obtained by minimizing the genera of three orientable handle bodiesHandlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
— with no intersection between their interiors— which decompose the manifold as far as the Heegaard
Heegaard splitting
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
genus need only two.
That is, a decomposition
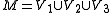 with
with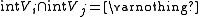
for
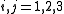 and being
and being 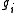 the genus of
the genus of 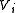 .
.For orientable spaces,
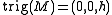 ,
,where
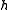 is
is 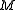 's Heegaard genus.
's Heegaard genus.For non-orientable spaces the
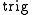 has the form
has the form 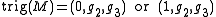
depending on the
image of the first Stiefel–Whitney characteristic class
Stiefel–Whitney class
In mathematics, in particular in algebraic topology and differential geometry, the Stiefel–Whitney class is an example of a \mathbb Z_2characteristic class associated to real vector bundles.-General presentation:...
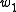 under a Bockstein homomorphism
under a Bockstein homomorphismBockstein homomorphism
In homological algebra, the Bockstein homomorphism, introduced by , is a connecting homomorphism associated with a short exact sequenceof abelian groups, when they are introduced as coefficients into a chain complex C, and which appears in the homology groups as a homomorphism reducing degree by...
, respectively for
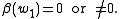
It has been proved that the number
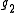 has a relation with the concept of Stiefel–Whitney surface, that is, an orientable surface
has a relation with the concept of Stiefel–Whitney surface, that is, an orientable surface 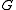 which is embedded in
which is embedded in 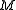 , has minimal genus and represents the first Stiefel–Whitney class under the duality map
, has minimal genus and represents the first Stiefel–Whitney class under the duality map 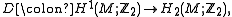 , that is,
, that is, 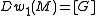 . If
. If 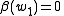 then
then 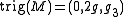 , and if
, and if 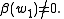
then
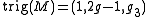 .
.
