Hyperbolic Dehn surgery
Encyclopedia
In mathematics
, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifold
s from a given cusped hyperbolic 3-manifold. Hyperbolic Dehn surgery exists only in dimension three and is one which distinguishes hyperbolic geometry
in three dimensions from other dimensions.
Such an operation is often also called hyperbolic Dehn filling, as Dehn surgery
proper refers to a "drill and fill" operation on a link which consists of drilling out a neighborhood of the link and then filling back in with solid tori. Hyperbolic Dehn surgery actually only involves "filling".
We will generally assume that a hyperbolic 3-manifold is complete.
Suppose M is a cusped hyperbolic 3-manifold with n cusps. M can be thought of, topologically, as the interior of a compact manifold with toral boundary. Suppose we have chosen a meridian and longitude for each boundary torus, i.e. simple closed curves that are generators for the fundamental group of the torus. Let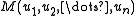
denote the manifold obtained from M by filling in the i-th boundary torus with a solid torus using the slope 
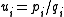where each pair 
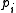and 
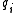are coprime integers. We allow a 
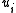to be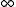 
which means we do not fill in that cusp, i.e. do the "empty" Dehn filling. So M = 
.
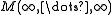We equip the space H of finite volume hyperbolic 3-manifolds with the geometric topology.
Thurston's hyperbolic Dehn surgery theorem states: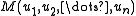
is hyperbolic as long as a finite set of slopes 
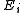is avoided for the i-th cusp for each i. In addition, 
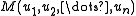converges to M in H as all 
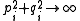for all 
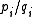corresponding to non-empty Dehn fillings 
.
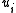This theorem is due to William Thurston
and fundamental to the theory of hyperbolic 3-manifolds. It shows that nontrivial limits exist in H. Troels Jorgensen's study of the geometric topology further shows that all nontrivial limits arise by Dehn filling as in the theorem.
Another important result by Thurston is that volume decreases under hyperbolic Dehn filling. In fact, the theorem states that volume decreases under topological Dehn filling, assuming of course that the Dehn-filled manifold is hyperbolic. The proof relies on basic properties of the Gromov norm
.
Jørgensen also showed that the volume function on this space is a continuous
, proper
function. Thus by the previous results, nontrivial limits in H are taken to nontrivial limits in the set of volumes. In fact, one can further conclude, as did Thurston, that the set of volumes of finite volume hyperbolic 3-manifolds has ordinal type
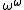. This result is known as the Thurston-Jørgensen theorem. Further work characterizing this set was done by Gromov.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifold
Hyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
s from a given cusped hyperbolic 3-manifold. Hyperbolic Dehn surgery exists only in dimension three and is one which distinguishes hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
in three dimensions from other dimensions.
Such an operation is often also called hyperbolic Dehn filling, as Dehn surgery
Dehn surgery
In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a specific construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link...
proper refers to a "drill and fill" operation on a link which consists of drilling out a neighborhood of the link and then filling back in with solid tori. Hyperbolic Dehn surgery actually only involves "filling".
We will generally assume that a hyperbolic 3-manifold is complete.
Suppose M is a cusped hyperbolic 3-manifold with n cusps. M can be thought of, topologically, as the interior of a compact manifold with toral boundary. Suppose we have chosen a meridian and longitude for each boundary torus, i.e. simple closed curves that are generators for the fundamental group of the torus. Let
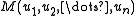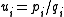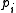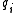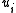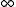denote the manifold obtained from M by filling in the i-th boundary torus with a solid torus using the slope where each pair and are coprime integers. We allow a to be which means we do not fill in that cusp, i.e. do the "empty" Dehn filling. So M = 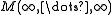.We equip the space H of finite volume hyperbolic 3-manifolds with the geometric topology.
Thurston's hyperbolic Dehn surgery theorem states:
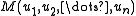is hyperbolic as long as a finite set of slopes 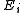is avoided for the i-th cusp for each i. In addition, converges to M in H as all 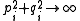for all 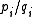corresponding to non-empty Dehn fillings 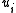.This theorem is due to William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
and fundamental to the theory of hyperbolic 3-manifolds. It shows that nontrivial limits exist in H. Troels Jorgensen's study of the geometric topology further shows that all nontrivial limits arise by Dehn filling as in the theorem.
Another important result by Thurston is that volume decreases under hyperbolic Dehn filling. In fact, the theorem states that volume decreases under topological Dehn filling, assuming of course that the Dehn-filled manifold is hyperbolic. The proof relies on basic properties of the Gromov norm
Gromov norm
In mathematics, the Gromov norm of a compact oriented n-manifold is a norm on the homology given by minimizing the sum of the absolute values of the coefficients over all singular chains representing a cycle...
.
Jørgensen also showed that the volume function on this space is a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, proper
Proper map
In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
function. Thus by the previous results, nontrivial limits in H are taken to nontrivial limits in the set of volumes. In fact, one can further conclude, as did Thurston, that the set of volumes of finite volume hyperbolic 3-manifolds has ordinal type
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
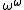. This result is known as the Thurston-Jørgensen theorem. Further work characterizing this set was done by Gromov.