
Quantum triviality
Encyclopedia
In a quantum field theory
, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. If
the only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting. Thus, surprisingly, a classical theory that appears to describe interacting particles can, when
realized as a quantum field theory, become a "trivial" theory of noninteracting free particles. This phenomenon is referred to as quantum triviality. Strong evidence supports the idea that a field theory involving only a scalar Higgs boson
is trivial in four spacetime dimensions, but the situation for realistic models including other particles in addition to the Higgs boson is not known in general. Nevertheless, because the Higgs boson plays a central role in the Standard Model
of particle physics
, the question of triviality in Higgs models is of great importance.
This Higgs triviality is similar to the Landau pole
problem in quantum electrodynamics
, where this quantum theory may be inconsistent at very high momentum scales unless the renormalized charge is set to zero, i.e., unless the field theory has no interactions. The Landau pole question is generally considered to be of minor academic interest for quantum electrodynamics because of the inaccessibly large momentum scale at which the inconsistency appears. This is not however the case in theories that involve the elementary scalar Higgs boson, as the momentum scale at which a "trivial" theory exhibits inconsistencies that may be accessible to present experimental efforts such as at the LHC
. In these Higgs theories, the interactions of the Higgs particle with itself are posited to generate the masses of the W and Z bosons
, as well as lepton
masses like those of the electron
and muon
. If realistic models of particle physics such as the Standard Model suffer from triviality issues, the idea of an elementary scalar Higgs particle may have to be modified or abandoned.
The situation becomes more complex in theories that involve other particles however. In fact, the addition of other particles can turn a trivial theory into a nontrivial one, at the cost of introducing constraints. Depending on the details of the theory, the Higgs mass can be bounded or even predictable. These quantum triviality constraints are in sharp contrast to the picture one derives at the classical level, where the Higgs mass is a free parameter.
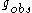 with the “bare” charge
with the “bare” charge 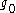

where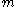 is the mass of the particle, and
is the mass of the particle, and 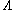 is the momentum cut-off. If
is the momentum cut-off. If  is finite, then
is finite, then  tends to zero in the limit of infinite cut-off
tends to zero in the limit of infinite cut-off 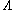 . In fact, the proper interpretation of Eq.1 consists in its inversion, so that
. In fact, the proper interpretation of Eq.1 consists in its inversion, so that  (related to the length scale
(related to the length scale 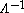 ) is chosen to give a correct value of
) is chosen to give a correct value of 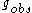 :
:
The growth of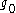 with
with 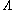 invalidates Eqs. 1 & 2 in the region
invalidates Eqs. 1 & 2 in the region 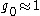 (since they were obtained for
(since they were obtained for 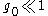 ) and existence of the “Landau pole" in Eq.2 has no physical sense. The actual behavior of the charge
) and existence of the “Landau pole" in Eq.2 has no physical sense. The actual behavior of the charge 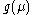 as a function of the momentum scale
as a function of the momentum scale  is determined by the Gell-Mann–Low equation
is determined by the Gell-Mann–Low equation
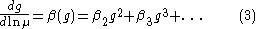
which gives Eqs.1,2 if it is integrated under conditions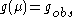 for
for 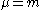 and
and 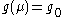 for
for  , when only the term with
, when only the term with  is retained in the right hand side. The general behavior of
is retained in the right hand side. The general behavior of 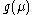 depends on the appearance of the function
depends on the appearance of the function  . According to classification by Bogoliubov and Shirkov, there are three qualitatively different situations:
. According to classification by Bogoliubov and Shirkov, there are three qualitatively different situations:
(a) if has a zero at the finite value
has a zero at the finite value 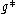 , then growth of
, then growth of 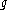 is saturated, i.e.
is saturated, i.e. 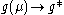 for
for 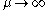 ;
;
(b) if is non-alternating and behaves as
is non-alternating and behaves as 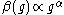 with
with 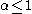 for large
for large 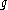 , then the growth of
, then the growth of 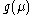 continues to infinity;
continues to infinity;
(c) if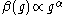 with
with  for large
for large  , then
, then 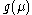 is divergent at finite value
is divergent at finite value  and the real Landau pole arises: the theory is internally inconsistent due to indeterminacy of
and the real Landau pole arises: the theory is internally inconsistent due to indeterminacy of 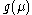 for
for  .
.
The latter case corresponds to the quantum triviality in full theory (beyond its perturbation context), as can be seen by a reductio ad absurdum
. Indeed, if is finite, the theory is internally inconsistent. The only way to avoid it, is to tend
is finite, the theory is internally inconsistent. The only way to avoid it, is to tend  to infinity, which is possible only for
to infinity, which is possible only for 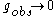 .
.
Formula (1) is interpreted differently in the theory of critical phenomena. In this case, and
and 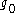 have a direct physical sense, being related to the lattice spacing and the coefficient in the effective Landau Hamiltonian. The trivial theory with
have a direct physical sense, being related to the lattice spacing and the coefficient in the effective Landau Hamiltonian. The trivial theory with 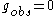 is obtained in the limit
is obtained in the limit 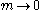 , which corresponds to the critical point. Such triviality has a physical sense and corresponds to absence of interaction between large-scale fluctuations of the order parameter. The fundamental question arises, if such triviality holds for arbitrary (and not only small) values of
, which corresponds to the critical point. Such triviality has a physical sense and corresponds to absence of interaction between large-scale fluctuations of the order parameter. The fundamental question arises, if such triviality holds for arbitrary (and not only small) values of 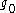 ? This question was investigated by Kenneth G. Wilson using the real-space renormalization group and strong evidence for the positive answer was obtained. Subsequent numerical investigations of the lattice field theory
? This question was investigated by Kenneth G. Wilson using the real-space renormalization group and strong evidence for the positive answer was obtained. Subsequent numerical investigations of the lattice field theory
confirmed Wilson’s conclusion.
However, it should be noted that “Wilson triviality” signifies only that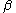 -function is non-alternating and has not non-trivial zeros: it excludes only the case (a) in the Bogoliubov and Shirkov classification. The “true” quantum triviality is a more strong property, corresponding to the case (c). If “Wilson triviality” is confirmed by numerous investigations and can be considered as firmly established, the evidence of “true triviality” is scarce and allows a different interpretation. As a result, the question of whether the Standard Model
-function is non-alternating and has not non-trivial zeros: it excludes only the case (a) in the Bogoliubov and Shirkov classification. The “true” quantum triviality is a more strong property, corresponding to the case (c). If “Wilson triviality” is confirmed by numerous investigations and can be considered as firmly established, the evidence of “true triviality” is scarce and allows a different interpretation. As a result, the question of whether the Standard Model
of particle physics
is nontrivial (and whether elementary scalar Higgs particles can exist) remains an important unresolved question. The evidence in favor of its positive solution has appeared recently
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. If
the only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting. Thus, surprisingly, a classical theory that appears to describe interacting particles can, when
realized as a quantum field theory, become a "trivial" theory of noninteracting free particles. This phenomenon is referred to as quantum triviality. Strong evidence supports the idea that a field theory involving only a scalar Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
is trivial in four spacetime dimensions, but the situation for realistic models including other particles in addition to the Higgs boson is not known in general. Nevertheless, because the Higgs boson plays a central role in the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, the question of triviality in Higgs models is of great importance.
This Higgs triviality is similar to the Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
problem in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, where this quantum theory may be inconsistent at very high momentum scales unless the renormalized charge is set to zero, i.e., unless the field theory has no interactions. The Landau pole question is generally considered to be of minor academic interest for quantum electrodynamics because of the inaccessibly large momentum scale at which the inconsistency appears. This is not however the case in theories that involve the elementary scalar Higgs boson, as the momentum scale at which a "trivial" theory exhibits inconsistencies that may be accessible to present experimental efforts such as at the LHC
LHC
LHC may refer to:* Large Hadron Collider, a particle accelerator and collider located on the Franco-Swiss border near Geneva, SwitzerlandLHC also may refer to:* La hora Chanante, a Spanish comedy television show...
. In these Higgs theories, the interactions of the Higgs particle with itself are posited to generate the masses of the W and Z bosons
W and Z bosons
The W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
, as well as lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
masses like those of the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
and muon
Muon
The muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
. If realistic models of particle physics such as the Standard Model suffer from triviality issues, the idea of an elementary scalar Higgs particle may have to be modified or abandoned.
The situation becomes more complex in theories that involve other particles however. In fact, the addition of other particles can turn a trivial theory into a nontrivial one, at the cost of introducing constraints. Depending on the details of the theory, the Higgs mass can be bounded or even predictable. These quantum triviality constraints are in sharp contrast to the picture one derives at the classical level, where the Higgs mass is a free parameter.
Triviality and the renormalization group
The first evidence of possible triviality of quantum field theories was obtained by Landau, Abrikosov, Khalatnikov who obtained the following relation of the observable charge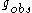 with the “bare” charge
with the “bare” charge 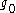

where
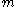 is the mass of the particle, and
is the mass of the particle, and 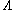 is the momentum cut-off. If
is the momentum cut-off. If  is finite, then
is finite, then  tends to zero in the limit of infinite cut-off
tends to zero in the limit of infinite cut-off 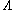 . In fact, the proper interpretation of Eq.1 consists in its inversion, so that
. In fact, the proper interpretation of Eq.1 consists in its inversion, so that  (related to the length scale
(related to the length scale 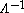 ) is chosen to give a correct value of
) is chosen to give a correct value of 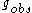 :
:The growth of
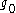 with
with 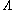 invalidates Eqs. 1 & 2 in the region
invalidates Eqs. 1 & 2 in the region 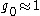 (since they were obtained for
(since they were obtained for 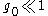 ) and existence of the “Landau pole" in Eq.2 has no physical sense. The actual behavior of the charge
) and existence of the “Landau pole" in Eq.2 has no physical sense. The actual behavior of the charge 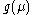 as a function of the momentum scale
as a function of the momentum scale  is determined by the Gell-Mann–Low equation
is determined by the Gell-Mann–Low equationRenormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
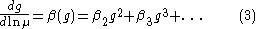
which gives Eqs.1,2 if it is integrated under conditions
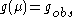 for
for 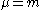 and
and 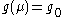 for
for  , when only the term with
, when only the term with  is retained in the right hand side. The general behavior of
is retained in the right hand side. The general behavior of 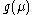 depends on the appearance of the function
depends on the appearance of the function  . According to classification by Bogoliubov and Shirkov, there are three qualitatively different situations:
. According to classification by Bogoliubov and Shirkov, there are three qualitatively different situations:(a) if
 has a zero at the finite value
has a zero at the finite value 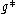 , then growth of
, then growth of 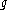 is saturated, i.e.
is saturated, i.e. 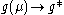 for
for 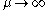 ;
;(b) if
 is non-alternating and behaves as
is non-alternating and behaves as 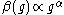 with
with 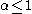 for large
for large 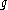 , then the growth of
, then the growth of 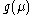 continues to infinity;
continues to infinity;(c) if
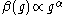 with
with  for large
for large  , then
, then 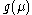 is divergent at finite value
is divergent at finite value  and the real Landau pole arises: the theory is internally inconsistent due to indeterminacy of
and the real Landau pole arises: the theory is internally inconsistent due to indeterminacy of 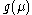 for
for  .
.The latter case corresponds to the quantum triviality in full theory (beyond its perturbation context), as can be seen by a reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
. Indeed, if
 is finite, the theory is internally inconsistent. The only way to avoid it, is to tend
is finite, the theory is internally inconsistent. The only way to avoid it, is to tend  to infinity, which is possible only for
to infinity, which is possible only for 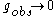 .
.Formula (1) is interpreted differently in the theory of critical phenomena. In this case,
 and
and 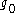 have a direct physical sense, being related to the lattice spacing and the coefficient in the effective Landau Hamiltonian. The trivial theory with
have a direct physical sense, being related to the lattice spacing and the coefficient in the effective Landau Hamiltonian. The trivial theory with 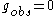 is obtained in the limit
is obtained in the limit 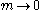 , which corresponds to the critical point. Such triviality has a physical sense and corresponds to absence of interaction between large-scale fluctuations of the order parameter. The fundamental question arises, if such triviality holds for arbitrary (and not only small) values of
, which corresponds to the critical point. Such triviality has a physical sense and corresponds to absence of interaction between large-scale fluctuations of the order parameter. The fundamental question arises, if such triviality holds for arbitrary (and not only small) values of 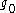 ? This question was investigated by Kenneth G. Wilson using the real-space renormalization group and strong evidence for the positive answer was obtained. Subsequent numerical investigations of the lattice field theory
? This question was investigated by Kenneth G. Wilson using the real-space renormalization group and strong evidence for the positive answer was obtained. Subsequent numerical investigations of the lattice field theoryLattice field theory
In physics, lattice field theory is the study of lattice models of quantum field theory, that is, of field theory on a spacetime that has been discretized onto a lattice. Although most lattice field theories are not exactly solvable, they are of tremendous appeal because they can be studied by...
confirmed Wilson’s conclusion.
However, it should be noted that “Wilson triviality” signifies only that
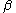 -function is non-alternating and has not non-trivial zeros: it excludes only the case (a) in the Bogoliubov and Shirkov classification. The “true” quantum triviality is a more strong property, corresponding to the case (c). If “Wilson triviality” is confirmed by numerous investigations and can be considered as firmly established, the evidence of “true triviality” is scarce and allows a different interpretation. As a result, the question of whether the Standard Model
-function is non-alternating and has not non-trivial zeros: it excludes only the case (a) in the Bogoliubov and Shirkov classification. The “true” quantum triviality is a more strong property, corresponding to the case (c). If “Wilson triviality” is confirmed by numerous investigations and can be considered as firmly established, the evidence of “true triviality” is scarce and allows a different interpretation. As a result, the question of whether the Standard ModelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
is nontrivial (and whether elementary scalar Higgs particles can exist) remains an important unresolved question. The evidence in favor of its positive solution has appeared recently


