Mass gap
Encyclopedia
In quantum field theory
, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest particle.
Since exact energy eigenstates are infinitely spread out and are therefore usually excluded from a formal mathematical description, a stronger definition is that the mass gap is the greatest lower bound of the energy of any state which is orthogonal to the vacuum.
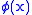, we can say that the theory has a mass gap if the two-point function
has the property
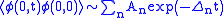
with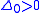
being the lowest energy value in the spectrum of the Hamiltonian and thus the mass gap. This quantity, easy to generalize to other fields, is what is generally measured in lattice computations. It was proved in this way that Yang-Mills theory develops a mass gap. The corresponding time-ordered value, the propagator
, will have the property
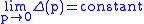
with the constant being finite. A typical example is offered by a free massive particle and, in this case, the constant has the value 1/m2. In the same limit, the propagator for a massless particle is singular.
or Higgs mechanism
. In the former case, one has to cope with the appearance of massless excitations, Goldstone boson
s, that are removed in the latter case due to gauge freedom. Quantization preserves this property.
A quartic massless scalar field theory develops a mass gap already at classical level. Let us consider the equation
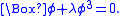
This equation has the exact solution
-- where
and 
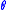are integration constants, and sn is a Jacobi elliptic function
-- provided
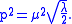
At the classical level, a mass gap appears while, at quantum level, one has a tower of excitations and this property of the theory is preserved after quantization in the limit of momenta going to zero.
While lattice computations have suggested that Yang-Mills theory indeed has a mass gap and a tower of excitations, a theoretical proof is still missing. This is one of the Clay Institute
Millennium problems
and it remains an open problem. Such states for Yang-Mills theory should be physical states, named glueball
s, and should be observable in the laboratory.
holds, at this stage we exclude gauge theories
, the spectral density function can take a very simple form with a discrete spectrum starting with a mass gap
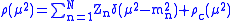
being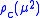
the contribution from multi-particle part of the spectrum. In this case, the propagator will take the simple form
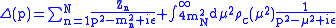
being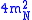
approximatively the starting point of the multi-particle sector. Now, using the fact that
we arrive at the following conclusion for the constants in the spectral density
.
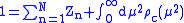This could not be true in a gauge theory
. Rather it must be proved that a Källén-Lehmann representation for the propagator
holds also for this case. Absence of multi-particle contributions implies that the theory is trivial
, as no bound states appear in the theory and so there is no interaction, even if the theory has a mass gap. In this case we have immediately the propagator
just setting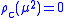
in the formulas above.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest particle.
Since exact energy eigenstates are infinitely spread out and are therefore usually excluded from a formal mathematical description, a stronger definition is that the mass gap is the greatest lower bound of the energy of any state which is orthogonal to the vacuum.
Mathematical definitions
For a given real field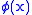, we can say that the theory has a mass gap if the two-point functionCorrelation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
has the property
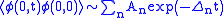
with
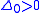being the lowest energy value in the spectrum of the Hamiltonian and thus the mass gap. This quantity, easy to generalize to other fields, is what is generally measured in lattice computations. It was proved in this way that Yang-Mills theory develops a mass gap. The corresponding time-ordered value, the propagatorPropagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
, will have the property
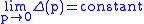
with the constant being finite. A typical example is offered by a free massive particle and, in this case, the constant has the value 1/m2. In the same limit, the propagator for a massless particle is singular.
Examples from classical theories
An example of mass gap arising for massless theories, already at the classical level, can be seen in spontaneous breaking of symmetrySpontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
or Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
. In the former case, one has to cope with the appearance of massless excitations, Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
s, that are removed in the latter case due to gauge freedom. Quantization preserves this property.
A quartic massless scalar field theory develops a mass gap already at classical level. Let us consider the equation
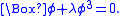
This equation has the exact solution
-- where
and 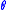are integration constants, and sn is a Jacobi elliptic functionJacobi's elliptic functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...
-- provided
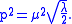
At the classical level, a mass gap appears while, at quantum level, one has a tower of excitations and this property of the theory is preserved after quantization in the limit of momenta going to zero.
While lattice computations have suggested that Yang-Mills theory indeed has a mass gap and a tower of excitations, a theoretical proof is still missing. This is one of the Clay Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
Millennium problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
and it remains an open problem. Such states for Yang-Mills theory should be physical states, named glueball
Glueball
In particle physics, a glueball is a hypothetical composite particle. It consists solely of gluon particles, without valence quarks. Such a state is possible because gluons carry color charge and experience the strong interaction...
s, and should be observable in the laboratory.
Källén-Lehmann representation
If Källén-Lehmann spectral representationKällén-Lehmann spectral representation
Källén-Lehmann spectral representation gives a general expression for the two-point function of an interacting quantum field theory as a sum of free propagators. It was discovered by Gunnar Källén and Harry Lehmann independently...
holds, at this stage we exclude gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, the spectral density function can take a very simple form with a discrete spectrum starting with a mass gap
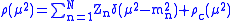
being
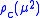the contribution from multi-particle part of the spectrum. In this case, the propagator will take the simple form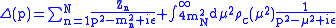being
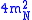approximatively the starting point of the multi-particle sector. Now, using the fact thatwe arrive at the following conclusion for the constants in the spectral density
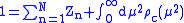.This could not be true in a gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
. Rather it must be proved that a Källén-Lehmann representation for the propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
holds also for this case. Absence of multi-particle contributions implies that the theory is trivial
Quantum triviality
In a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
, as no bound states appear in the theory and so there is no interaction, even if the theory has a mass gap. In this case we have immediately the propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
just setting
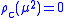in the formulas above.External links
- Sadun, Lorenzo. Yang-Mills and the Mass Gap. Video lecture outlining the nature of the mass gap problem within the Yang-Mills formulation.
- Mass gaps for scalar field theories on Dispersive Wiki
See also
- Yang–Mills existence and mass gapYang–Mills existence and mass gapIn mathematics, the Yang-Mills existence and mass gap problem is an unsolved problem and one of the seven Millennium Prize Problems defined by the Clay Mathematics Institute which has offered a prize of US$1,000,000 to a person solving it....
- Scalar field theoryScalar field theoryIn theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
- Spontaneous symmetry breakingSpontaneous symmetry breakingSpontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
- Correlation function (quantum field theory)Correlation function (quantum field theory)In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
- Källén-Lehmann spectral representationKällén-Lehmann spectral representationKällén-Lehmann spectral representation gives a general expression for the two-point function of an interacting quantum field theory as a sum of free propagators. It was discovered by Gunnar Källén and Harry Lehmann independently...
- Quantum trivialityQuantum trivialityIn a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...