Aharonov-Bohm effect
Encyclopedia
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–Bohm effect, is a quantum mechanical
phenomenon in which an electrically charged
particle
is affected by an electromagnetic field
(E, B), despite being confined to a region in which both the magnetic field
B and electric field
E are zero. The underlying mechanism is the coupling
of the electromagnetic potential with the complex phase of a charged particle's wavefunction
, and the Aharonov–Bohm effect is accordingly illustrated by interference experiments
.
The most commonly described case, sometimes called the Aharonov–Bohm solenoid effect, takes place when the wave function of a charged particle passing around a long solenoid
experiences a phase shift
as a result of the enclosed magnetic field, despite the magnetic field being negligible in the region through which the particle passes and the particle's wavefunction being negligible inside the solenoid. This phase shift has been observed experimentally. There are also magnetic Aharonov–Bohm effects on bound energies and scattering cross sections, but these cases have not been experimentally tested. An electric Aharonov–Bohm phenomenon was also predicted, in which a charged particle is affected by regions with different electrical potentials but zero electric field, but this has no experimental confirmation yet. A separate "molecular" Aharonov–Bohm effect was proposed for nuclear motion in multiply connected regions, but this has been argued to be a different kind of geometric phase
as it is "neither nonlocal nor topological", depending only on local quantities along the nuclear path.
Werner Ehrenberg and Raymond E. Siday first predicted the effect in 1949, and similar effects were later published by Yakir Aharonov
and David Bohm
in 1959. After publication of the 1959 paper, Bohm was informed of Ehrenberg and Siday's work, which was acknowledged and credited in Bohm and Aharanov's subsequent 1961 paper. A general review can be found in Peshkin and Tonomura (1989).
of a scalar potential (Coulomb's electrostatic potential, entirely analogous, mathematically, to the classical gravitational potential) and a stationary magnetic field as the curl of a vector potential (then a new concept - the idea of a scalar potential was already well accepted by analogy with the gravitational potential). The language of potentials generalised seamlessly to the fully dynamic case but, since all physical effects were describable in terms of the fields which were the derivatives of the potentials, potentials (unlike fields) were not uniquely determined by physical effects (potentials were only defined up to an arbitrary additive constant electrostatic potential and an irrotational stationary magnetic vector potential).
The Aharonov–Bohm effect is important conceptually because it bears on three issues apparent in the recasting of (Maxwell
's) classical electromagnetic theory
as a gauge theory
, which before the advent of quantum mechanics could be argued to be a mathematical reformulation with no physical consequences. The Aharonov-Bohm thought experiment
s and their experimental realization imply that the issues were not just philosophical.
The three issues are:
Because of reasons like these, the Aharonov–Bohm effect was chosen by the New Scientist
magazine as one of the "seven wonders of the quantum world".
s, E and B, were physical and that the electromagnetic potentials, Φ and A, were purely mathematical constructs (Φ and A being non-unique, in addition to not appearing in the Lorentz Force
formula). The non-uniqueness of the electromagnetic potentials is a manifestation of electromagnetic gauge freedom, with the electric and magnetic fields and forces being gauge invariant and therefore directly observable (the E and B fields do appear in the Lorentz force formula).
, is not just a computational aid to the Newtonian approach
, based on forces. Thus the Aharonov–Bohm effect validates the view that forces are an incomplete way to formulate physics, and potential energies must be used instead. In fact Richard Feynman
complained that he had been taught electromagnetism from the perspective of E and B, and he wished later in life he had been taught to think in terms of the A field instead, as this would be more fundamental. In Feynman's path-integral view of dynamics
, the A field directly changes the phase of an electron wave function, and it is these changes in phase that lead to measurable quantities.
, A, must be used instead. By Stokes' theorem
, the magnitude of the Aharonov–Bohm effect can be calculated using the E and B fields alone, or using the A 4-potential alone. But when using just the E and B fields, the effect depends on the field values in a region from which the test particle is excluded, not only classically but also quantum mechanically. In contrast, when using just the electromagnetic four-potential A the effect only depends on the A potential in the region where the test particle is allowed. Therefore we can either abandon the principle of locality
(which most physicists are reluctant to do) or we are forced to accept that the electromagnetic 4-potential - composed of Φ and A - offers a more complete description of electromagnetism than the electric and magnetic fields can. In classical electromagnetism
the two descriptions were equivalent. With the addition of quantum theory, though, the electromagnetic potentials Φ and A are seen as being more fundamental. The E and B fields can be derived from the 4-potential, but the 4-potential, by gauge freedom, cannot be derived from the E and B fields.
for the electromagnetic potential, of which the magnetic vector potential A forms part.
Electromagnetic theory implies that a particle with electric charge q travelling along some path P in a region with zero magnetic field
B, but non-zero A (by
), acquires a phase shift 
, given in SI
units by
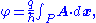
Therefore particles, with the same start and end points, but travelling along two different routes will acquire a phase difference Δφ determined by the magnetic flux
ΦB through the area between the paths (via Stokes' theorem
and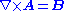
), and given by:
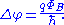
In quantum mechanics
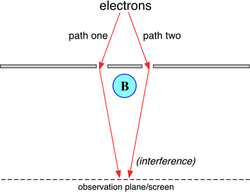
the same particle can travel between two points by a variety of paths. Therefore this phase difference can be observed by placing a solenoid
between the slits of a double-slit experiment
(or equivalent). An ideal solenoid (i.e. infinitely long and with a perfectly uniform current distribution) encloses a magnetic field B, but does not produce any magnetic field outside of its cylinder, and thus the charged particle (e.g. an electron
) passing outside experiences no magnetic field B. However, there is a (curl-free) vector potential A outside the solenoid with an enclosed flux, and so the relative phase of particles passing through one slit or the other is altered by whether the solenoid current is turned on or off. This corresponds to an observable shift of the interference fringes on the observation plane.
The same phase effect is responsible for the quantized-flux
requirement in superconducting
loops. This quantization occurs because the superconducting wave function must be single valued: its phase difference Δφ around a closed loop must be an integer multiple of 2π (with the charge for the electron Cooper pair
s), and thus the flux Φ must be a multiple of h/2e. The superconducting flux quantum was actually predicted prior to Aharonov and Bohm, by F. London in 1948 using a phenomenological model.
The magnetic Aharonov–Bohm effect was experimentally confirmed by Osakabe et al. (1986), following much earlier work summarized in Olariu and Popèscu (1984). Its scope and application continues to expand. Webb et al. (1985) demonstrated Aharonov–Bohm oscillations in ordinary, non-superconducting metallic rings; for a discussion, see Schwarzschild (1986) and Imry & Webb (1989). Bachtold et al. (1999) detected the effect in carbon nanotubes; for a discussion, see Kong et al. (2004).
argument that the existence of a magnetic monopole
can be accommodated by the existing magnetic source-free Maxwell's equations
if both electric and magnetic charges are quantized.
A magnetic monopole implies a mathematical singularity in the vector potential, which can be expressed as a Dirac string
of infinitesimal diameter that contains the equivalent of all of the 4πg flux from a monopole "charge" g. The Dirac string starts from, and terminates on, a magnetic monopole. Thus, assuming the absence of an infinite-range scattering effect by this arbitrary choice of singularity, the requirement of single-valued wave functions (as above) necessitates charge-quantization. That is,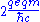
must be an integer (in cgs
units) for any electric charge qe and magnetic charge qm.
Like the electromagnetic potential A the Dirac string is not gauge invariant (it moves around with fixed endpoints under a gauge transformation) and so is also not directly measurable.
From the Schrödinger equation
, the phase of an eigenfunction with energy E goes as
. The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V (zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
where t is the time spent in the potential.
The initial theoretical proposal for this effect suggested an experiment where charges pass through conducting cylinders along two paths, which shield the particles from external electric fields in the regions where they travel, but still allow a varying potential to be applied by charging the cylinders. This proved difficult to realize, however. Instead, a different experiment was proposed involving a ring geometry interrupted by tunnel barriers, with a bias voltage V relating the potentials of the two halves of the ring. This situation results in an Aharonov–Bohm phase shift as above, and was observed experimentally in 1998.
s and the Aharonov–Bohm effect. Application of these rings used as light capacitors or buffers includes photonic computing
and communications technology. Analysis and measurement of geometric phases in mesoscopic rings is ongoing.
of a flat complex line bundle
. The U(1)-connection
on this line bundle is given by the electromagnetic four-potential
A as
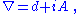where d means partial derivation in the Minkowski space
. The curvature form
of the connection,
, is the electromagnetic field strength
, where
is the 1-form corresponding to the four-potential. The holonomy
of the connection,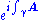
around a closed loop 
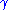is, as a consequence of Stokes' theorem
, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is
; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding number
around the tube and is, by definition, the monodromy of the flat connection.
In any simply connected region outside of the tube we can find a gauge transformation
(acting on wave functions and connections) that gauges away the vector potential. However, if the monodromy is non trivial, there is no such gauge transformation for the whole outside region.
If we want to ignore the physics inside the conductor and only describe the physics in the outside region, it becomes natural to mathematically describe the quantum electron by a section in a complex line bundle with an "external" connection
rather than an external EM field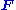 
(by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor 
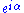, which results in a shift in the interference pattern.
Effects with similar mathematical interpretation can be found in other fields. For example, in classical statistical physics, quantization of a molecular motor motion in a stochastic environment can be interpreted as an Aharonov–Bohm effect induced by a gauge field acting in the space of control parameters.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
phenomenon in which an electrically charged
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
particle
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
is affected by an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
(E, B), despite being confined to a region in which both the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B and electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E are zero. The underlying mechanism is the coupling
Coupling (physics)
In physics, two systems are coupled if they are interacting with each other. Of special interest is the coupling of two vibratory systems by means of springs or magnetic fields, etc...
of the electromagnetic potential with the complex phase of a charged particle's wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
, and the Aharonov–Bohm effect is accordingly illustrated by interference experiments
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
.
The most commonly described case, sometimes called the Aharonov–Bohm solenoid effect, takes place when the wave function of a charged particle passing around a long solenoid
Solenoid
A solenoid is a coil wound into a tightly packed helix. In physics, the term solenoid refers to a long, thin loop of wire, often wrapped around a metallic core, which produces a magnetic field when an electric current is passed through it. Solenoids are important because they can create...
experiences a phase shift
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
as a result of the enclosed magnetic field, despite the magnetic field being negligible in the region through which the particle passes and the particle's wavefunction being negligible inside the solenoid. This phase shift has been observed experimentally. There are also magnetic Aharonov–Bohm effects on bound energies and scattering cross sections, but these cases have not been experimentally tested. An electric Aharonov–Bohm phenomenon was also predicted, in which a charged particle is affected by regions with different electrical potentials but zero electric field, but this has no experimental confirmation yet. A separate "molecular" Aharonov–Bohm effect was proposed for nuclear motion in multiply connected regions, but this has been argued to be a different kind of geometric phase
Geometric phase
In classical and quantum mechanics, the geometric phase, Pancharatnam–Berry phase , Pancharatnam phase or most commonly Berry phase, is a phase acquired over...
as it is "neither nonlocal nor topological", depending only on local quantities along the nuclear path.
Werner Ehrenberg and Raymond E. Siday first predicted the effect in 1949, and similar effects were later published by Yakir Aharonov
Yakir Aharonov
Yakir Aharonov is an Israeli physicist specializing in quantum physics. He is a Professor of Theoretical Physics and the James J. Farley Professor of Natural Philosophy at Chapman University in California. He is also a distinguished professor in Perimeter Institute.He also serves as a professor...
and David Bohm
David Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
in 1959. After publication of the 1959 paper, Bohm was informed of Ehrenberg and Siday's work, which was acknowledged and credited in Bohm and Aharanov's subsequent 1961 paper. A general review can be found in Peshkin and Tonomura (1989).
Significance
In the 18th and 19th centuries, physics was dominated by Newtonian dynamics, with its emphasis on forces. Electromagnetic phenomena were elucidated by a series of experiments involving the measurement of forces between charges, currents and magnets in various configurations. Eventually, a description arose according to which charges, currents and magnets acted as local sources of propagating force fields, which then acted on other charges and currents locally through the Lorentz force law. In this framework, because one of the observed properties of the electric field was that it was irrotational, and one of the observed properties of the magnetic field was that it was divergenceless, it was possible to express an electrostatic field as the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar potential (Coulomb's electrostatic potential, entirely analogous, mathematically, to the classical gravitational potential) and a stationary magnetic field as the curl of a vector potential (then a new concept - the idea of a scalar potential was already well accepted by analogy with the gravitational potential). The language of potentials generalised seamlessly to the fully dynamic case but, since all physical effects were describable in terms of the fields which were the derivatives of the potentials, potentials (unlike fields) were not uniquely determined by physical effects (potentials were only defined up to an arbitrary additive constant electrostatic potential and an irrotational stationary magnetic vector potential).
The Aharonov–Bohm effect is important conceptually because it bears on three issues apparent in the recasting of (Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
's) classical electromagnetic theory
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
as a gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, which before the advent of quantum mechanics could be argued to be a mathematical reformulation with no physical consequences. The Aharonov-Bohm thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
s and their experimental realization imply that the issues were not just philosophical.
The three issues are:
- whether potentials are "physical" or a just convenient tool for calculating force fields;
- whether actionAction (physics)In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
principles are fundamental; - the principle of localityPrinciple of localityIn physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
.
Because of reasons like these, the Aharonov–Bohm effect was chosen by the New Scientist
New Scientist
New Scientist is a weekly non-peer-reviewed English-language international science magazine, which since 1996 has also run a website, covering recent developments in science and technology for a general audience. Founded in 1956, it is published by Reed Business Information Ltd, a subsidiary of...
magazine as one of the "seven wonders of the quantum world".
Potentials vs. fields
The Aharonov–Bohm effect illustrates the physicality of electromagnetic potentials, Φ and A, whereas previously it was possible to argue that only the electromagnetic fieldElectromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
s, E and B, were physical and that the electromagnetic potentials, Φ and A, were purely mathematical constructs (Φ and A being non-unique, in addition to not appearing in the Lorentz Force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
formula). The non-uniqueness of the electromagnetic potentials is a manifestation of electromagnetic gauge freedom, with the electric and magnetic fields and forces being gauge invariant and therefore directly observable (the E and B fields do appear in the Lorentz force formula).
Global action vs. local forces
Similarly, the Aharonov–Bohm effect illustrates that the Lagrangian approach to dynamics, based on energiesAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
, is not just a computational aid to the Newtonian approach
Newtonian dynamics
In physics, the Newtonian dynamics is understood as the dynamics of a particle or a small body according to Newton's laws of motion.-Mathematical generalizations:...
, based on forces. Thus the Aharonov–Bohm effect validates the view that forces are an incomplete way to formulate physics, and potential energies must be used instead. In fact Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
complained that he had been taught electromagnetism from the perspective of E and B, and he wished later in life he had been taught to think in terms of the A field instead, as this would be more fundamental. In Feynman's path-integral view of dynamics
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
, the A field directly changes the phase of an electron wave function, and it is these changes in phase that lead to measurable quantities.
Locality of electromagnetic effects
The Aharonov–Bohm effect shows that the local E and B fields do not contain full information about the electromagnetic field, and the electromagnetic four-potentialElectromagnetic four-potential
The electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
, A, must be used instead. By Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
, the magnitude of the Aharonov–Bohm effect can be calculated using the E and B fields alone, or using the A 4-potential alone. But when using just the E and B fields, the effect depends on the field values in a region from which the test particle is excluded, not only classically but also quantum mechanically. In contrast, when using just the electromagnetic four-potential A the effect only depends on the A potential in the region where the test particle is allowed. Therefore we can either abandon the principle of locality
Principle of locality
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
(which most physicists are reluctant to do) or we are forced to accept that the electromagnetic 4-potential - composed of Φ and A - offers a more complete description of electromagnetism than the electric and magnetic fields can. In classical electromagnetism
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
the two descriptions were equivalent. With the addition of quantum theory, though, the electromagnetic potentials Φ and A are seen as being more fundamental. The E and B fields can be derived from the 4-potential, but the 4-potential, by gauge freedom, cannot be derived from the E and B fields.
Magnetic solenoid effect
The magnetic Aharonov–Bohm effect can be seen as a result of the requirement that quantum physics be invariant with respect to the gauge choiceGauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
for the electromagnetic potential, of which the magnetic vector potential A forms part.
Electromagnetic theory implies that a particle with electric charge q travelling along some path P in a region with zero magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B, but non-zero A (by
), acquires a phase shift , given in SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units by
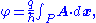
Therefore particles, with the same start and end points, but travelling along two different routes will acquire a phase difference Δφ determined by the magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
ΦB through the area between the paths (via Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
and
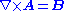), and given by: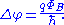Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
the same particle can travel between two points by a variety of paths. Therefore this phase difference can be observed by placing a solenoid
Solenoid
A solenoid is a coil wound into a tightly packed helix. In physics, the term solenoid refers to a long, thin loop of wire, often wrapped around a metallic core, which produces a magnetic field when an electric current is passed through it. Solenoids are important because they can create...
between the slits of a double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
(or equivalent). An ideal solenoid (i.e. infinitely long and with a perfectly uniform current distribution) encloses a magnetic field B, but does not produce any magnetic field outside of its cylinder, and thus the charged particle (e.g. an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
) passing outside experiences no magnetic field B. However, there is a (curl-free) vector potential A outside the solenoid with an enclosed flux, and so the relative phase of particles passing through one slit or the other is altered by whether the solenoid current is turned on or off. This corresponds to an observable shift of the interference fringes on the observation plane.
The same phase effect is responsible for the quantized-flux
Magnetic flux quantum
The magnetic flux quantum Φ0 is the quantum of magnetic flux passing through a superconductor. The phenomenon of flux quantization was discovered B. S. Deaver and W. M. Fairbank and, independently, by R. Doll and M. Nabauer, in 1961...
requirement in superconducting
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
loops. This quantization occurs because the superconducting wave function must be single valued: its phase difference Δφ around a closed loop must be an integer multiple of 2π (with the charge for the electron Cooper pair
Cooper pair
In condensed matter physics, a Cooper pair or BCS pair is two electrons that are bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper...
s), and thus the flux Φ must be a multiple of h/2e. The superconducting flux quantum was actually predicted prior to Aharonov and Bohm, by F. London in 1948 using a phenomenological model.
The magnetic Aharonov–Bohm effect was experimentally confirmed by Osakabe et al. (1986), following much earlier work summarized in Olariu and Popèscu (1984). Its scope and application continues to expand. Webb et al. (1985) demonstrated Aharonov–Bohm oscillations in ordinary, non-superconducting metallic rings; for a discussion, see Schwarzschild (1986) and Imry & Webb (1989). Bachtold et al. (1999) detected the effect in carbon nanotubes; for a discussion, see Kong et al. (2004).
Monopoles and Dirac strings
The magnetic Aharonov–Bohm effect is also closely related to Dirac'sPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
argument that the existence of a magnetic monopole
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
can be accommodated by the existing magnetic source-free Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
if both electric and magnetic charges are quantized.
A magnetic monopole implies a mathematical singularity in the vector potential, which can be expressed as a Dirac string
Dirac string
In physics, a Dirac string is a fictitious one-dimensional curve in space, conceived of by the physicist Paul Dirac, stretching between two Dirac magnetic monopoles with opposite magnetic charges, or from one magnetic monopole out to infinity. The gauge potential cannot be defined on the Dirac...
of infinitesimal diameter that contains the equivalent of all of the 4πg flux from a monopole "charge" g. The Dirac string starts from, and terminates on, a magnetic monopole. Thus, assuming the absence of an infinite-range scattering effect by this arbitrary choice of singularity, the requirement of single-valued wave functions (as above) necessitates charge-quantization. That is,
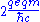must be an integer (in cgsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
units) for any electric charge qe and magnetic charge qm.
Like the electromagnetic potential A the Dirac string is not gauge invariant (it moves around with fixed endpoints under a gauge transformation) and so is also not directly measurable.
Electric effect
Just as the phase of the wave function depends upon the magnetic vector potential, it also depends upon the scalar electric potential. By constructing a situation in which the electrostatic potential varies for two paths of a particle, through regions of zero electric field, an observable Aharonov–Bohm interference phenomenon from the phase shift has been predicted; again, the absence of an electric field means that, classically, there would be no effect.From the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, the phase of an eigenfunction with energy E goes as
. The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V (zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:where t is the time spent in the potential.
The initial theoretical proposal for this effect suggested an experiment where charges pass through conducting cylinders along two paths, which shield the particles from external electric fields in the regions where they travel, but still allow a varying potential to be applied by charging the cylinders. This proved difficult to realize, however. Instead, a different experiment was proposed involving a ring geometry interrupted by tunnel barriers, with a bias voltage V relating the potentials of the two halves of the ring. This situation results in an Aharonov–Bohm phase shift as above, and was observed experimentally in 1998.
Aharonov–Bohm nano rings
Nano rings were created by accident while intending to make quantum dots. They have interesting optical properties associated with excitonExciton
An exciton is a bound state of an electron and hole which are attracted to each other by the electrostatic Coulomb force. It is an electrically neutral quasiparticle that exists in insulators, semiconductors and some liquids...
s and the Aharonov–Bohm effect. Application of these rings used as light capacitors or buffers includes photonic computing
Photonic computing
Today's computers use the movement of electrons in-and-out of transistors to do logic. Optical or Photonic computing is intended to use photons or light particles, produced by lasers or diodes, in place of electrons...
and communications technology. Analysis and measurement of geometric phases in mesoscopic rings is ongoing.
Mathematical interpretation
In the terms of modern differential geometry, the Aharonov–Bohm effect can be understood to be the monodromyMonodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
of a flat complex line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
. The U(1)-connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on this line bundle is given by the electromagnetic four-potential
Electromagnetic four-potential
The electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
A as
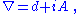where d means partial derivation in the Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. The curvature formCurvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
of the connection,
, is the electromagnetic field strengthField strength
In physics, the field strength of a field is the magnitude of its vector value.In theoretical physics, field strength is another name for the curvature form...
, where
is the 1-form corresponding to the four-potential. The holonomyHolonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
of the connection,
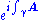around a closed loop 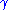is, as a consequence of Stokes' theoremStokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is
; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberWinding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
around the tube and is, by definition, the monodromy of the flat connection.
In any simply connected region outside of the tube we can find a gauge transformation
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
(acting on wave functions and connections) that gauges away the vector potential. However, if the monodromy is non trivial, there is no such gauge transformation for the whole outside region.
If we want to ignore the physics inside the conductor and only describe the physics in the outside region, it becomes natural to mathematically describe the quantum electron by a section in a complex line bundle with an "external" connection
rather than an external EM field 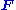(by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor 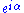, which results in a shift in the interference pattern.Effects with similar mathematical interpretation can be found in other fields. For example, in classical statistical physics, quantization of a molecular motor motion in a stochastic environment can be interpreted as an Aharonov–Bohm effect induced by a gauge field acting in the space of control parameters.
See also
- Geometric phaseGeometric phaseIn classical and quantum mechanics, the geometric phase, Pancharatnam–Berry phase , Pancharatnam phase or most commonly Berry phase, is a phase acquired over...
- Hannay angleHannay angleIn classical mechanics, the Hannay angle is a mechanics analogue of the Berry phase. It was named after John Hannay of the University of Bristol, UK.-Example:...
- Wannier functionWannier functionThe Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier.The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes...
- Berry phase
- Wilson loopWilson loopIn gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
- Winding numberWinding numberIn mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
- Aharonov-Casher effectAharonov-Casher effectThe Aharonov–Casher effect is a quantum mechanical phenomenon in which a traveling magnetic dipole is affected by electric field. It is dual to Aharonov-Bohm effect, in which the quantum phase of charged particle depends on side of magnetic flux tube it comes through. In Aharonov–Casher effect, the...