
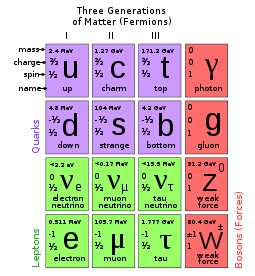
Standard model (basic details)
Encyclopedia
- For a basic description, see the article on the Standard ModelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
.
This is a detailed description of the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
(SM) of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
. It describes how the lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s, quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s, gauge boson
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s and the Higgs particle
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
fit together. It gives an outline of the main physics that the theory describes, and new directions in which it is moving.
It may be helpful to read this article along with the companion overview of the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
.
A chiral gauge theory
The chiralityChirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
projections of a Dirac field ψ are
-
- "Left" chirality: ψL = ½(1 - γ5)ψ
- "Right" chirality: ψR = ½(1 + γ5)ψ
where γ5 is the fifth gamma matrix.
These are needed because the SM is a chiral gauge theory, i.e., the two helicities are treated differently.
This article uses the Dirac basis instead of the Weyl basis for describing spinors. The Weyl basis is more convenient because there is no natural correspondence between the left-handed and right-handed fermion fields other than that generated dynamically through the Yukawa couplings after the Higgs field has acquired a vacuum expectation value (VEV
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
). In consulting common texts on the standard model one should expect to find the Weyl basis used.
Right handed singlets, left handed doublets
Under the weak isospinWeak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
SU(2)
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
the left-handed and right-handed chiralities
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
have different charges
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
. The left-handed particles are weak-isospin doublets (2), whereas the right-handed are singlets (1). The right-handed neutrino does not exist in the standard model. (However, in some extensions of the standard model it does.) The up-type quarks are charge 2/3 quarks: u, c, t. The charge -1/3 quarks (d, s, b) are called down-type quarks. The charged leptons (e, μ, τ) are denoted by l, and their corresponding neutrinos by ν. The theory contains
-
- the left handed doublet of quarks QL = (uL, dL) and leptons EL = (νlL, lL)
- the right handed singlets of quarks uR and dR and the charged leptons lR.
When the Standard Model was written down, there was no evidence for neutrino mass. Now, however, a series of experiments
including Super-Kamiokande
Super-Kamiokande
Super-Kamiokande is a neutrino observatory which is under Mount Kamioka near the city of Hida, Gifu Prefecture, Japan...
have indicated that neutrinos indeed have a tiny mass. This fact can be simply accommodated in the Standard Model by adding a right-handed neutrino. This, however, is not strictly necessary. For example, the dimension 5 operator
 also leads to neutrino oscillation
also leads to neutrino oscillationNeutrino oscillation
Neutrino oscillation is a quantum mechanical phenomenon predicted by Bruno Pontecorvowhereby a neutrino created with a specific lepton flavor can later be measured to have a different flavor. The probability of measuring a particular flavor for a neutrino varies periodically as it propagates...
s.
This pattern is replicated in the next generations. We introduce a generation label i = 1,2,3 and write ui to denote the three generations of up-type quarks, and similarly for the down type quarks. The left-handed quark doublet also carries a generation index, QiL, as does the lepton doublet, EiL.
Why this?
What dictates this form of the weak isospin charges? The coupling of a right-handed neutrinoNeutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
to matter in weak interactions was ruled out by experiment long ago. Benjamin Lee
Benjamin W. Lee
Benjamin Whisoh Lee or Ben Lee, was a Korean-American theoretical physicist...
and J. Zinn-Justin, and Gerardus 't Hooft
Gerardus 't Hooft
Gerardus 't Hooft is a Dutch theoretical physicist and professor at Utrecht University, the Netherlands. He shared the 1999 Nobel Prize in Physics with his thesis advisor Martinus J. G...
and Martinus Veltman
Martinus J. G. Veltman
Martinus Justinus Godefriedus Veltman is a Dutch theoretical physicist. He shared the 1999 Nobel Prize in physics with his former student Gerardus 't Hooft for their work on particle theory.-Biography:...
in 1972 suggested the inclusion of left and right-handed fields into the same multiplet
Multiplet
In group theory, a multiplet is formally a group representation of an algebra.In physics, multiplet can mean:* A group of related spectral lines* A group of related subatomic particles...
. This possibility has been ruled out by experiment. This leaves the construction given above.
For the lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s, the gauge group can then be SU(2)l × U(1)L × U(1)R. The two U(1) factors can be combined into U(1)Y × U(1)l where l is the lepton number
Lepton number
In particle physics, the lepton number is the number of leptons minus the number of antileptons.In equation form,so all leptons have assigned a value of +1, antileptons −1, and non-leptonic particles 0...
. Gauging of the lepton number is ruled out by experiment, leaving only the possible gauge group SU(2)L × U(1)Y. A similar argument in the quark sector also gives the same result for the electroweak theory. This form of the theory developed from a suggestion by Sheldon Glashow
Sheldon Lee Glashow
Sheldon Lee Glashow is a Nobel Prize winning American theoretical physicist. He is the Metcalf Professor of Mathematics and Physics at Boston University.-Birth and education:...
in 1961 and extended independently by Steven Weinberg
Steven Weinberg
Steven Weinberg is an American theoretical physicist and Nobel laureate in Physics for his contributions with Abdus Salam and Sheldon Glashow to the unification of the weak force and electromagnetic interaction between elementary particles....
and Abdus Salam
Abdus Salam
Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk (Urdu: محمد عبد السلام, pronounced , (January 29, 1926– November 21, 1996) was a Pakistani theoretical physicist and Nobel laureate in Physics for his work on the electroweak unification of the...
in 1967 (and was anticipated in rudimentary form by Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
in 1957).
The gauge field part
The gauge group has already been described. Now one needs the fieldField (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
s. The correct kinetic term for a spin-1 field with local gauge invariance is built from the (non-Abelian) field strength tensor

in terms of the gauge field
 , where the subscript
, where the subscript  runs over spacetime dimensions (0 to 3) and the superscript
runs over spacetime dimensions (0 to 3) and the superscript  over the elements of the adjoint representation of the gauge group, and
over the elements of the adjoint representation of the gauge group, and  is the gauge coupling constant
is the gauge coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
. The quantity
 is the structure constant of the gauge group, defined by the commutator
is the structure constant of the gauge group, defined by the commutator  . In an Abelian group
. In an Abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, since the generators
 all commute with each other, the structure constants vanish, and the field tensor takes its usual Abelian form.
all commute with each other, the structure constants vanish, and the field tensor takes its usual Abelian form.We need to introduce three gauge fields corresponding to each of the subgroups
 —
—
- The gluon field tensor will be denoted by
 , where the index
, where the index  labels elements of the 8 representation of colour SU(3)Special unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
labels elements of the 8 representation of colour SU(3)Special unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
. The strong coupling constant will be labelled or
or  , the former where there is any ambiguity. The observations leading to the discovery of this part of the SM are discussed in the article in quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, the former where there is any ambiguity. The observations leading to the discovery of this part of the SM are discussed in the article in quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
. - The notation
 will be used for the gauge field tensor of SU(2)Special unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
will be used for the gauge field tensor of SU(2)Special unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
where a runs over the 3 generators of this group. The coupling will always be denoted by . The gauge field will be denoted by
. The gauge field will be denoted by  .
. - The gauge field tensor for the U(1) of weak hyperchargeWeak hyperchargeThe weak hypercharge in particle physics is a conserved quantum number relating the electrical charge and the third component of weak isospin, and is similar to the Gell-Mann–Nishijima formula for the hypercharge of strong interactions...
will be denoted by , the coupling by
, the coupling by  , and the gauge field by
, and the gauge field by  .
.
The Gauge Field Lagrangian
Using the field strength tensors, the kinetic terms for the electroweak gauge fields are
The standard model Lagrangian consists of another similar term constructed using the gluon field tensor.
The W, Z and photon
The charged W bosonW and Z bosons
The W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
s are the linear combinations
 .
.Z boson
W and Z bosons
The W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
s (
 ) and photon
) and photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s (
 ) are mixtures of
) are mixtures of  and
and  . The
. Theprecise mixture is determined by the Weinberg angle
Weinberg angle
The Weinberg angle or weak mixing angle is a parameter in the Weinberg–Salam theory of the electroweak interaction, and is usually denoted as θW...
 :
: and
and 
with
 .
.The electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
Q, weak isospin
Weak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
T3 (aka Tz) and weak hypercharge
Weak hypercharge
The weak hypercharge in particle physics is a conserved quantum number relating the electrical charge and the third component of weak isospin, and is similar to the Gell-Mann–Nishijima formula for the hypercharge of strong interactions...
YW are related by

Note: usually weak hypercharge is scaled so that

which is a formally equivalent to Gell-Mann–Nishijima formula
Gell-Mann–Nishijima formula
The Gell-Mann–Nishijima formula relates the baryon number B, the strangeness S, the isospin I3 of hadrons to the charge Q. It was originally given by Kazuhiko Nishijima and Tadao Nakano in 1953, and lead to the proposal of strangeness as a concept, which Nishijima originally called "eta-charge"...
.
The charged and neutral current couplings
The charged currents are
are
These charged currents are precisely those that entered the Fermi theory of beta decay. The action contains the charge current piece
It will be discussed later in this article that the W boson becomes massive, and for energy much less than this mass, the effective theory becomes the current-current interaction of the Fermi theory.
However, gauge invariance now requires that the component
 of the gauge field also be coupled to a current that lies in the triplet of SU(2). However, this mixes with the U(1), and another current in that sector is needed. These currents must be uncharged in order to conserve charge. So we require the neutral currents
of the gauge field also be coupled to a current that lies in the triplet of SU(2). However, this mixes with the U(1), and another current in that sector is needed. These currents must be uncharged in order to conserve charge. So we require the neutral currents
The neutral current piece in the Lagrangian is then
There are no mass terms for the fermions. Everything else will come through the scalar (Higgs) sector.
Quantum chromodynamics
Here Ta stands for the generators of SU(3) colour. The mass term in QCD arises from interactions in the Higgs sector.
The Higgs field
One requires masses for the W, Z, quarks and leptons. Recent experiments have also shown that the neutrinoNeutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
has a mass. However, the details of the mechanism that give the neutrinos a mass are not yet clear. So this article deals with the classic version of the SM (circa 1990s, when neutrino masses could be neglected with impunity).
The Yukawa terms
Giving a mass to a Dirac field requires a term in the Lagrangian that couples the left and right helicities. A complex scalar doublet (charge 2) Higgs field, is introduced, which couples through the Yukawa interaction
is introduced, which couples through the Yukawa interactionYukawa interaction
In particle physics, Yukawa's interaction, named after Hideki Yukawa, is an interaction between a scalar field \phi and a Dirac field \Psi of the typeV \approx g\bar\Psi \phi \Psi or g \bar \Psi \gamma^5 \phi \Psi ....
where
 are 3×3 matrices of Yukawa couplings, with the ij term giving the coupling of the generations i and j.
are 3×3 matrices of Yukawa couplings, with the ij term giving the coupling of the generations i and j.Symmetry breaking
The Higgs part of the Lagrangian iswhere
 and
and  , so that the mechanism of spontaneous symmetry breaking
, so that the mechanism of spontaneous symmetry breakingSpontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
can be used.
In a unitarity gauge
Unitarity gauge
In theoretical physics, the unitarity gauge or unitary gauge is a particular choice of a gauge fixing in a gauge theory with a spontaneous symmetry breaking. In this gauge, the scalar fields responsible for the Higgs mechanism are transformed into a basis in which their Goldstone boson components...
one can set
 and make
and make  real. Then
real. Then  is the non-vanishing vacuum expectation value
is the non-vanishing vacuum expectation valueVacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the Higgs field. Putting this into
 , a mass term for the fermions is obtained, with a mass matrix
, a mass term for the fermions is obtained, with a mass matrix  . From
. From  , quadratic terms in
, quadratic terms in  and
and  arise, which give masses to the W and Z bosons
arise, which give masses to the W and Z bosons
Including neutrino mass
As mentioned earlier, in the SM classic there are no right-handed neutrinos. The same mechanism as the quarks would then give masses to the electrons, but because of the missing right-handed neutrino the neutrinos remain massless. Small changes can also accommodate massive neutrinos. Two approaches are possible—- Add
 , and give a mass term as usual (this is called a Dirac mass)
, and give a mass term as usual (this is called a Dirac mass) - Write a Majorana mass term by combining
 with its complex conjugate
with its complex conjugate
See seesaw mechanism
Seesaw mechanism
In theoretical physics, the seesaw mechanism is a mechanism within grand unification theory, and in particular in theories of neutrino masses and neutrino oscillation, where it can be used to explain the smallness of observed neutrino masses relative to those of quarks and leptons.There are several...
.
These alternatives can easily lead beyond the SM.
The GIM mechanism and the CKM matrix
The Yukawa couplings for the quarks are not required to have any particular symmetry, so they cannot be diagonalized by unitary transformationUnitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
s. However, they can be diagonalized by separate unitary matrices acting on the two sides (this process is called a singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
). In other words one can find diagonal matrices
 ::
::
This matrix V is called the Cabibbo-Kobayashi-Maskawa (CKM) matrix. The matrix is usually not diagonal, and therefore causes mixing of the quark flavours. It also gives rise to CP-violations in the SM.
See also
- Overview of standard modelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physicsParticle physicsParticle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
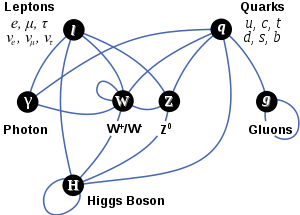
- Weak interactions, Fermi theory of beta decay and electroweak theory
- Strong interactionStrong interactionIn particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
s, flavourFlavour (particle physics)In particle physics, flavour or flavor is a quantum number of elementary particles. In quantum chromodynamics, flavour is a global symmetry...
, quark modelQuark modelIn physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks which give rise to the quantum numbers of the hadrons....
and quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions... - For open questions, see quark matterQCD matterQuark matter or QCD matter refers to any of a number of theorized phases of matter whose degrees of freedom include quarks and gluons. These theoretical phases would occur at extremely high temperatures and densities, billions of times higher than can be produced in equilibrium in laboratories...
, CP violation and neutrino massNeutrinoA neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
es - noncommutative standard modelNoncommutative standard modelIn theoretical particle physics, the non-commutative Standard Model, mainly due to the French mathematician Alain Connes, uses his noncommutative geometry to devise an extension of the Standard Model to include a modified form of general relativity. This unification implies a few constraints on the...
- Beyond the Standard ModelBeyond the Standard ModelPhysics beyond the Standard Model refers to the theoretical developments needed to explain the deficiencies of the Standard Model, such as the origin of mass, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy...
- Weinberg angleWeinberg angleThe Weinberg angle or weak mixing angle is a parameter in the Weinberg–Salam theory of the electroweak interaction, and is usually denoted as θW...
- Electroweak interactionElectroweak interactionIn particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
- Fundamental interactionFundamental interactionIn particle physics, fundamental interactions are the ways that elementary particles interact with one another...











