
Dirac measure
Encyclopedia
In mathematics
, a Dirac measure is a measure
δx on a set X (with any σ-algebra of subset
s of X) defined by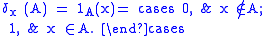
for a given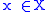 and any (measurable) set A ⊆ X.
and any (measurable) set A ⊆ X.
The Dirac measure is a probability measure
, and in terms of probability it represents the almost sure outcome x in the sample space X. We can also say that the measure is a single atom
at x; however, treating the Dirac measure as an atomic measure is not correct when we consider the sequential definition of Dirac delta, as the limit of a delta sequence. The Dirac measures are the extreme point
s of the convex set of probability measures on X.
The name is a back-formation from the Dirac delta function
, considered as a Schwartz distribution
, for example on the real line
; measures can be taken to be a special kind of distribution. The identity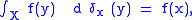
which, in the form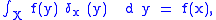
is often taken to be part of the definition of the "delta function", holds as a theorem of Lebesgue integration
.
Suppose that (X, T) is a topological space
and that Σ is at least as fine as the Borel σ-algebra σ(T) on X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Dirac measure is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
δx on a set X (with any σ-algebra of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X) defined by
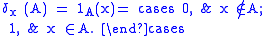
for a given
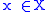 and any (measurable) set A ⊆ X.
and any (measurable) set A ⊆ X.The Dirac measure is a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
, and in terms of probability it represents the almost sure outcome x in the sample space X. We can also say that the measure is a single atom
Atom (measure theory)
In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure...
at x; however, treating the Dirac measure as an atomic measure is not correct when we consider the sequential definition of Dirac delta, as the limit of a delta sequence. The Dirac measures are the extreme point
Extreme point
In mathematics, an extreme point of a convex set S in a real vector space is a point in S which does not lie in any open line segment joining two points of S...
s of the convex set of probability measures on X.
The name is a back-formation from the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, considered as a Schwartz distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, for example on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
; measures can be taken to be a special kind of distribution. The identity
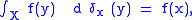
which, in the form
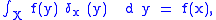
is often taken to be part of the definition of the "delta function", holds as a theorem of Lebesgue integration
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
.
Properties of the Dirac measure
Let δx denote the Dirac measure centred on some fixed point x in some measurable space (X, Σ).- δx is a probability measure, and hence a finite measure.
Suppose that (X, T) is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and that Σ is at least as fine as the Borel σ-algebra σ(T) on X.
- δx is a strictly positive measureStrictly positive measureIn mathematics, strict positivity is a concept in measure theory. Intuitively, a strictly positive measure is one that is "nowhere zero", or that it is zero "only on points".-Definition:...
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the topology T is such that x lies within every non-empty open set, e.g. in the case of the trivial topology {∅, X}. - Since δx is probability measure, it is also a locally finite measureLocally finite measureIn mathematics, a locally finite measure is a measure for which every point of the measure space has a neighbourhood of finite measure.-Definition:...
. - If X is a HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space with its Borel σ-algebra, then δx satisfies the condition to be an inner regular measureInner regular measureIn mathematics, an inner regular measure is one for which the measure of a set can be approximated from within by compact subsets.-Definition:...
, since singleton sets such as {x} are always compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Hence, δx is also a Radon measureRadon measureIn mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
. - Assuming that the topology T is fine enough that {x} is closed, which is the case in most applications, the supportSupport (measure theory)In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
of δx is {x}. (Otherwise, supp(δx) is the closure of {x} in (X, T).) Furthermore, δx is the only probability measure whose support is {x}. - If X is n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with its usual σ-algebra and n-dimensional Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
λn, then δx is a singular measureSingular measureIn mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A...
with respect to λn: simply decompose Rn as A = Rn \ {x} and B = {x} and observe that δx(A) = λn(B) = 0.

