Ultrastrong topology
Encyclopedia
In functional analysis
, the ultrastrong topology, or σ-strong topology, or strongest topology on the set B(H) of bounded operator
s on a Hilbert space
is the topology defined by the family of seminorms
for positive elements
of the predual
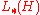that consists of trace class operators.
It was introduced by von Neumann in 1936.
For example, on any norm-bounded set the strong operator and ultrastrong topologies
are the same. The ultrastrong topology is stronger than the strong operator topology.
One problem with the strong operator topology is that the dual of B(H) with the strong operator topology is
"too small". The ultrastrong topology fixes this problem: the dual is the full predual
B*(H) of all trace class operators. In general the ultrastrong topology is better than the strong operator topology, but is more complicated to define so people usually use the strong operator topology if they can get away with it.
The ultrastrong topology can be obtained from the strong operator topology as follows.
If H1 is a separable infinite dimensional Hilbert space
then B(H) can be embedded in B(H⊗H1) by tensoring with the identity map on H1. Then the restriction of the strong operator topology on
B(H⊗H1) is the ultrastrong topology of B(H).
Equivalently, it is given by the family of seminorms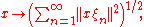
where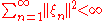
.
The adjoint map is not continuous in the ultrastrong topology. There is another topology called the ultrastrong* topology, which is the weakest topology stronger than the ultrastrong topology such that the adjoint map is continuous.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the ultrastrong topology, or σ-strong topology, or strongest topology on the set B(H) of bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is the topology defined by the family of seminorms
for positive elements
of the predualPredual
In mathematics, the predual of an object D is an object P whose dual space is D.For example, the predual of the space of bounded operators is the space of trace class operators. The predual of the space of differential forms is the space of chainlets....
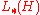that consists of trace class operators.It was introduced by von Neumann in 1936.
Relation with the strong (operator) topology
The ultrastrong topology is similar to the strong (operator) topology.For example, on any norm-bounded set the strong operator and ultrastrong topologies
are the same. The ultrastrong topology is stronger than the strong operator topology.
One problem with the strong operator topology is that the dual of B(H) with the strong operator topology is
"too small". The ultrastrong topology fixes this problem: the dual is the full predual
B*(H) of all trace class operators. In general the ultrastrong topology is better than the strong operator topology, but is more complicated to define so people usually use the strong operator topology if they can get away with it.
The ultrastrong topology can be obtained from the strong operator topology as follows.
If H1 is a separable infinite dimensional Hilbert space
then B(H) can be embedded in B(H⊗H1) by tensoring with the identity map on H1. Then the restriction of the strong operator topology on
B(H⊗H1) is the ultrastrong topology of B(H).
Equivalently, it is given by the family of seminorms
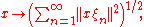
where
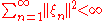. The adjoint map is not continuous in the ultrastrong topology. There is another topology called the ultrastrong* topology, which is the weakest topology stronger than the ultrastrong topology such that the adjoint map is continuous.
See also
- Topologies on the set of operators on a Hilbert space
- ultraweak topologyUltraweak topologyIn functional analysis, a branch of mathematics, the ultraweak topology, also called the weak-* topology, or weak-* operator topology or σ-weak topology, on the set B of bounded operators on a Hilbert space is the weak-* topology obtained from the predual B* of B, the trace class operators on H...
- strong operator topologyStrong operator topologyIn functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...