
Continuous geometry
Encyclopedia
In mathematics, continuous geometry is an analogue of complex projective geometry
introduced by , where instead of the dimension of a subspace being in a discrete set 0, 1, ..., n, it can be an element of the unit interval [0,1]. Von Neumann was motivated by his discovery of von Neumann algebra
s with a dimension function taking a continuous range of dimensions, and the first example of a continuous geometry other than projective space was the projections of the hyperfinite type II factor
.
A continuous geometry is a lattice
L with the following properties
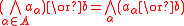
where A is a directed set and if α<β then aα <aβ, and the same condition with ∧ and ∨ reversed.
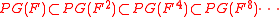
Two elements a and b of L are called perspective, written a∼b, if they have a common complement. This is an equivalence relation on L; the proof that it is transitive is quite hard.
The equivalence classes A, B, ... of L have a total order on them defined by A≤B if there is some a in A and b in B with a≤b. (This need not hold for all a in A and b in B.)
The dimension function D from L to the unit interval is defined as follows.
The image of D can be the whole unit interval, or the set of numbers 0, 1/n, 2/n, ..., 1 for some positive integer n. Two elements of L have the same image under D if and only if they are perspective, so it gives an injection from the equivalence classes to a subset of the unit interval. The dimension function D has the properties:
states that a projective geometry of dimension at least 3 is isomorphic to the projective geometry of a vector space over a division ring. This can be restated as saying that the subspaces in the projective geometry correspond to the principal right ideals of a matrix algebra over a division ring.
Von Neumann generalized this to continuous geometries, and more generally to complemented modular lattices, as follows . His theorem states that if a complemented modular lattice L has order at least 4, then the elements of L correspond to the principal right ideals of a von Neumann regular ring
. More precisely if the lattice has order n then the von Neumann regular ring can be taken to be an n by n matrix ring Mn(R) over another von Neumann regular ring R. Here a complemented modular lattice has order n if it has a homogeneous basis of n elements, where a basis is n elements a1,...an such that ai∧aj= 0 if i≠j, and a1∨...∨an=1, and a basis is called homogeneous if any two elements are perspective. The order of a lattice need not be unique; for example, any lattice has order 1. The condition that the lattice has order at least 4 corresponds to the condition that the dimension is at least 3 in the Veblen–Young theorem, as a projective space has dimension at least 3 if and only if it has a set of at least 4 independent points.
Conversely, the principal right ideals of a von Neumann regular ring form a complemented modular lattice .
Suppose that R is a von Neumann regular ring and L its lattice of principal right ideals, so that L is a complemented modular lattice. Von Neumann showed that L is a continuous geometry if and only if R is an irreducible complete rank ring
.
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
introduced by , where instead of the dimension of a subspace being in a discrete set 0, 1, ..., n, it can be an element of the unit interval [0,1]. Von Neumann was motivated by his discovery of von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
s with a dimension function taking a continuous range of dimensions, and the first example of a continuous geometry other than projective space was the projections of the hyperfinite type II factor
Hyperfinite type II factor
In mathematics, there are up to isomorphism exactly two hyperfinite type II factors; one infinite and one finite. Murray and von Neumann proved that up to isomorphism there is a unique von Neumann algebra that is a factor of type II1 and also hyperfinite; it is called the hyperfinite type II1...
.
Definition
Menger and Birkhoff gave axioms for projective geometry in terms of the lattice of linear subspaces of projective space. Von Neumann's axioms for continuous geometry are a weakened form of these axioms.A continuous geometry is a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
L with the following properties
- L is modularModular latticeIn the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
. - L is complete.
- The lattice operations ∧, ∨ satisfy a certain continuity property.
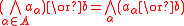
where A is a directed set and if α<β then aα <aβ, and the same condition with ∧ and ∨ reversed.
- Every element in L has a complement (not necessarily unique). A complement of an element a is an element b with a∧b=0, a∨b=1, where 0 and 1 are the minimal and maximal elements of L
- L is irreducible: this means that the only elements with unique complements are 0 and 1.
Examples
- Finite-dimensional complex projective space, or rather its set of linear subspaces, is a continuous geometry, with dimensions taking values in the discrete set {0, 1/n, 2/n, ..., 1}
- The projections of a finite type II von Neumann algebra form a continuous geometry with dimensions taking values in the unit interval [0,1]. showed that any orthocomplemented complete modular lattice is a continuous geometry.
- If V is a vector space over a field (or division ring) F, then there is a natural map from the lattice PG(V) of subspaces of V to the lattice of subspaces of V⊗F2 that multiplies dimensions by 2. So we can take a direct limit of
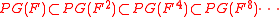
- This has a dimension function taking values all dyadic rationals between 0 and 1. Its completion is a continuous geometry containing elements of every dimension in [0,1]. This geometry was constructed by , and is called the continuous geometry over F.
Dimension
This section summarizes some of the results of . These results are similar to, and were motivated by, von Neumann's work on projections in von Neumann algebras.Two elements a and b of L are called perspective, written a∼b, if they have a common complement. This is an equivalence relation on L; the proof that it is transitive is quite hard.
The equivalence classes A, B, ... of L have a total order on them defined by A≤B if there is some a in A and b in B with a≤b. (This need not hold for all a in A and b in B.)
The dimension function D from L to the unit interval is defined as follows.
- If equivalence classes A and B contain elements a and b with a∧b=0 then their sum A+B is defined to be the equivalence class of a∨b. Otherwise the sum A+B is not defined. For a positive integer n, the product nA is defined to be the sum of n copies of A, if this sum is defined.
- For equivalence classes A and B with A not {0} the integer [B:A] is defined to be the unique integer n≥0 such that B = nA+C with C<B.
- For equivalence classes A and B with A not {0} the real number (B:A) is defined to be the limit of [B:C]/[A:C] as C runs though a minimal sequence: this means that either C contains a minimal nonzero element, or an infinite sequence of nonzero elements each of which is at most half the preceding one.
- D(a) is defined to be ({a}:{1}) where {a} and {1} are the equivalence classes containing a and 1.
The image of D can be the whole unit interval, or the set of numbers 0, 1/n, 2/n, ..., 1 for some positive integer n. Two elements of L have the same image under D if and only if they are perspective, so it gives an injection from the equivalence classes to a subset of the unit interval. The dimension function D has the properties:
- If a<b then D(a)<D(b)
- D(a∨b) + D(a∧b) = D(a)+D(b)
- D(a)=0 if and only if a=0, and D(a)=1 if and only if a=1
- 0≤D(a)≤1
Coordinatization theorem
In projective geometry, the Veblen–Young theoremVeblen–Young theorem
In mathematics, the Veblen–Young theorem, proved by , states that a projective space of dimension at least 3 can be constructed as the projective space associated to a vector space over a division ring....
states that a projective geometry of dimension at least 3 is isomorphic to the projective geometry of a vector space over a division ring. This can be restated as saying that the subspaces in the projective geometry correspond to the principal right ideals of a matrix algebra over a division ring.
Von Neumann generalized this to continuous geometries, and more generally to complemented modular lattices, as follows . His theorem states that if a complemented modular lattice L has order at least 4, then the elements of L correspond to the principal right ideals of a von Neumann regular ring
Von Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
. More precisely if the lattice has order n then the von Neumann regular ring can be taken to be an n by n matrix ring Mn(R) over another von Neumann regular ring R. Here a complemented modular lattice has order n if it has a homogeneous basis of n elements, where a basis is n elements a1,...an such that ai∧aj= 0 if i≠j, and a1∨...∨an=1, and a basis is called homogeneous if any two elements are perspective. The order of a lattice need not be unique; for example, any lattice has order 1. The condition that the lattice has order at least 4 corresponds to the condition that the dimension is at least 3 in the Veblen–Young theorem, as a projective space has dimension at least 3 if and only if it has a set of at least 4 independent points.
Conversely, the principal right ideals of a von Neumann regular ring form a complemented modular lattice .
Suppose that R is a von Neumann regular ring and L its lattice of principal right ideals, so that L is a complemented modular lattice. Von Neumann showed that L is a continuous geometry if and only if R is an irreducible complete rank ring
Rank ring
In mathematics, a rank ring is a ring with a real-valued rank function behaving like the rank of an endomorphism. introduced rank rings in his work on continuous geometry, and showed that the ring associated to a continuous geometry is a rank ring....
.

