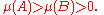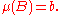Atom (measure theory)
Encyclopedia
In mathematics
, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure. A measure which has no atoms is called non-atomic or atomless.
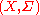 and a measure
and a measure
 on that space, a set
on that space, a set  in
in  is called an atom if
is called an atom if
and for any measurable subset of
of  with
with
one has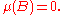
 with
with 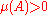 there exists a measurable subset B of A such that
there exists a measurable subset B of A such that
A non-atomic measure with at least one positive value has an infinite number of distinct values, as starting with a set A with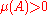 one can construct a decreasing sequence of measurable sets
one can construct a decreasing sequence of measurable sets
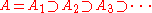
such that
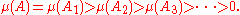
This may not be true for measures having atoms; see the first example above.
It turns out that non-atomic measures actually have a continuum
of values. It can be proved that if μ is a non-atomic measure and A is a measurable set with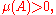 then for any real number b satisfying
then for any real number b satisfying
there exists a measurable subset B of A such that
This theorem is due to Wacław Sierpiński.
It is reminiscent of the intermediate value theorem
for continuous functions.
Sketch of proof of Sierpiński's theorem on non-atomic measures. A slightly stronger statement, which however makes the proof easier, is that if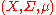 is a non-atomic measure space and
is a non-atomic measure space and 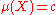 , there exists a function
, there exists a function 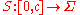 that is monotone with respect to inclusion, and a right-inverse to
that is monotone with respect to inclusion, and a right-inverse to  . That is, there exists a one-parameter family of measurable sets S(t) such that for all
. That is, there exists a one-parameter family of measurable sets S(t) such that for all 
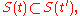

The proof easily follows from Zorn's lemma
applied to the set of all monotone partial sections to :
:
ordered by inclusion of graphs, It's then standard to show that every chain in
It's then standard to show that every chain in  has a maximal element, and that any maximal element of
has a maximal element, and that any maximal element of  has domain
has domain  proving the claim.
proving the claim.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure. A measure which has no atoms is called non-atomic or atomless.
Definition
Given a measurable space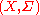 and a measure
and a measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
 on that space, a set
on that space, a set  in
in  is called an atom if
is called an atom ifand for any measurable subset
 of
of  with
withone has
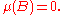
Examples
- Consider the set X={1, 2, ..., 9, 10} and let the sigma-algebra
 be the power set of X. Define the measure
be the power set of X. Define the measure  of a set to be its cardinality, that is, the number of elements in the set. Then, each of the singletons {i}, for i=1,2, ..., 9, 10 is an atom.
of a set to be its cardinality, that is, the number of elements in the set. Then, each of the singletons {i}, for i=1,2, ..., 9, 10 is an atom. - Consider the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. This measure has no atoms.
Non-atomic measures
A measure which has no atoms is called non-atomic. In other words, a measure is non-atomic if for any measurable set with
with 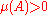 there exists a measurable subset B of A such that
there exists a measurable subset B of A such thatA non-atomic measure with at least one positive value has an infinite number of distinct values, as starting with a set A with
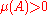 one can construct a decreasing sequence of measurable sets
one can construct a decreasing sequence of measurable sets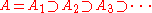
such that
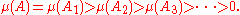
This may not be true for measures having atoms; see the first example above.
It turns out that non-atomic measures actually have a continuum
Continuum (theory)
Continuum theories or models explain variation as involving a gradual quantitative transition without abrupt changes or discontinuities. It can be contrasted with 'categorical' models which propose qualitatively different states.-In physics:...
of values. It can be proved that if μ is a non-atomic measure and A is a measurable set with
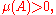 then for any real number b satisfying
then for any real number b satisfyingthere exists a measurable subset B of A such that
This theorem is due to Wacław Sierpiński.
It is reminiscent of the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
for continuous functions.
Sketch of proof of Sierpiński's theorem on non-atomic measures. A slightly stronger statement, which however makes the proof easier, is that if
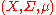 is a non-atomic measure space and
is a non-atomic measure space and 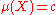 , there exists a function
, there exists a function 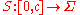 that is monotone with respect to inclusion, and a right-inverse to
that is monotone with respect to inclusion, and a right-inverse to  . That is, there exists a one-parameter family of measurable sets S(t) such that for all
. That is, there exists a one-parameter family of measurable sets S(t) such that for all 
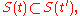

The proof easily follows from Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
applied to the set of all monotone partial sections to
 :
:
ordered by inclusion of graphs,
 It's then standard to show that every chain in
It's then standard to show that every chain in  has a maximal element, and that any maximal element of
has a maximal element, and that any maximal element of  has domain
has domain  proving the claim.
proving the claim.See also
- Atom (order theory) — an analogous concept in order theory
- Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
- Elementary eventElementary eventIn probability theory, an elementary event or atomic event is a singleton of a sample space. An outcome is an element of a sample space. An elementary event is a set containing exactly one outcome, not the outcome itself...
, also known as an atomic event