24-cell	Cantellated 24-cell	Cantitruncated 24-cell
Orthogonal projections in F4 Coxeter plane

In four-dimensional geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a cantellated 24-cell is a convex uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

, being a cantellation (a 2nd order truncation) of the regular 24-cell.

There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.

Cantellated 24-cell

Cantellated 24-cell
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t0,2{3,4,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Cells	144	24 (3.4.4.4) 24 (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... 96 (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
Faces	720	288 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 432 square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s
Edges	864
Vertices	288
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	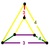Irreg. triangular prism
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	F4, [3,4,3]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
Uniform index	24 Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... 25 26 Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell....

The cantellated 24-cell is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

.

The boundary of the cantellated 24-cell is composed of
24 truncated octahedral

Truncated octahedron

In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....

 cells,
24 cuboctahedral

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

 cells and 96 triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

s.
Together they have 288 triangular faces, 432 square faces, 864 edges, and 288 vertices.

Construction

When the cantellation

Cantellation (geometry)

In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...

 process is applied to 24-cell,
each of the 24 octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

 becomes a small rhombicuboctahedron.
In addition however, since each octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

's edge was previously shared with two
other octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

, the separating edges form the three parallel edges of a
triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

 - 96 triangular prisms, since the 24-cell contains 96 edges.
Further, since each vertex was previously shared with 12 faces,
the vertex would split into 12 (24*12=288) new vertices.
Each group of 12 new vertices forms a cuboctahedron

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

.

Coordinates

The Cartesian coordinates of the vertices of the cantellated 24-cell having edge length 2 are all permutations of coordinates and sign of:
The permutations of the second set of coordinates coincide with the vertices of an inscribed runcitruncated tesseract.

The dual configuration has all permutations and signs of:

Structure

The 24 small rhombicuboctahedra are joined to each other via their triangular faces, to the cuboctahedra

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

 via their axial square faces, and to the triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

s via their off-axial square faces. The cuboctahedra are joined to the triangular prisms via their triangular faces. Each triangular prism is joined to two cuboctahedra at its two ends.

Images

Schlegel diagrams

Schlegel diagram

Showing 24 cuboctahedra Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... .

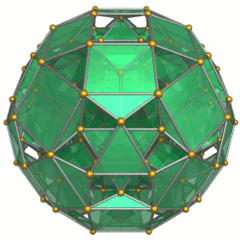Showing 96 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s.

Cantitruncated 24-cell

Cantitruncated 24-cell
Schlegel diagram, centered on truncated cuboctahedron
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t0,1,2{3,4,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Cells	144	24 4.6.8 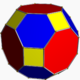 96 4.4.3 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....   24 3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....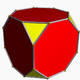
Faces	720	192{3} 288{4} 96{6} 144{8}
Edges	1152
Vertices	576
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	sphenoid Sphenoid Sphenoid may refer to:* In anatomy, the sphenoid bone* In geometry, a tetrahedron with mirror symmetry...
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	F4, [3,4,3]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
Uniform index	27 28 29

The cantitruncated 24-cell is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

 derived from the 24-cell. It is bounded by 24 great rhombicuboctahedra corresponding with the cells of a 24-cell, 24 truncated cube

Truncated cube

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

s corresponding with the cells of the dual 24-cell, and 96 triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

s corresponding with the edges of the first 24-cell.

Coordinates

The Cartesian coordinates of a cantitruncated 24-cell having edge length 2 are all permutations of coordinates and sign of:

(1,1+√2,1+2√2,3+3√2)

(0,2+√2,2+2√2,2+3√2)

The dual configuration has coordinates as all permutations and signs of:

(1,1+√2,1+√2,5+2√2)

(1,3+√2,3+√2,3+2√2)

(2,2+√2,2+√2,4+2√2)

Projections

Stereographic projection

Stereographic projection

The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...