
Total relation
Encyclopedia
In mathematics
, a binary relation
R over a set X is total if for all a and b in X, a is related to b or b is related to a (or both).
In mathematical notation
, this is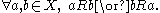
Total relations are sometimes said to have comparability.
.) The relation "is a proper subset of" is also not total.
.
If a transitive relation
is also total, it is a total preorder. If a partial order
is also total, it is a total order
.
A binary relation R over X is called connex if for all a and b in X such that a ≠ b, a is related to b or b is related to a (or both):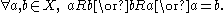
Connexity does not imply reflexivity. A strict partial order is a strict total order if and only if it is connex.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R over a set X is total if for all a and b in X, a is related to b or b is related to a (or both).
In mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
, this is
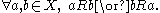
Total relations are sometimes said to have comparability.
Examples
For example, "is less than or equal to" is a total relation over the set of real numbers, because for two numbers either the first is less than or equal to the second, or the second is less than or equal to the first. On the other hand, "is less than" is not a total relation, since one can pick two equal numbers, and then neither the first is less than the second, nor is the second less than the first. (But note that "is less than" is a weak order which gives rise to a total order, namely "is less than or equal to". The relationship between strict orders and weak orders is discussed at partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
.) The relation "is a proper subset of" is also not total.
Properties and related notions
Totality implies reflexivityReflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
.
If a transitive relation
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
is also total, it is a total preorder. If a partial order
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
is also total, it is a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
.
A binary relation R over X is called connex if for all a and b in X such that a ≠ b, a is related to b or b is related to a (or both):
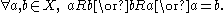
Connexity does not imply reflexivity. A strict partial order is a strict total order if and only if it is connex.

