Inductive dimension
Encyclopedia
In the mathematical field of topology
, the inductive dimension of a topological space
X is either of two values, the small inductive dimension ind(X) or the large inductive dimension Ind(X). These are based on the observation that, in n-dimensional Euclidean space
Rn, (n − 1)-dimensional sphere
s (that is, the boundaries
of n-dimensional balls) have dimension n − 1. Therefore it should be possible to define the dimension of a space inductively
in terms of the dimensions of the boundaries of suitable open set
s.
The small and large inductive dimensions are two of the three most usual ways of capturing the notion of "dimension" for a topological space, in a way that depends only on the topology (and not, say, on the properties of a metric space
). The other is the Lebesgue covering dimension
. The term "topological dimension" is ordinarily understood to refer to Lebesgue covering dimension. For "sufficiently nice" spaces, the three measures of dimension are equal.
Then inductively, ind(X) is the smallest n such that, for every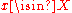
and every open set U containing x, there is an open V containing x, where the closure
of V is a subset
of U, such that the boundary of V has small inductive dimension less than or equal to n − 1. (In the case above, where X is Euclidean n-dimensional space, V will be chosen to be an n-dimensional ball centered at x.)
For the large inductive dimension, we restrict the choice of V still further; Ind(X) is the smallest n such that, for every closed
subset F of every open subset U of X, there is an open V in between (that is, F is a subset of V and the closure of V is a subset of U), such that the boundary of V has large inductive dimension less than or equal to n − 1.
be the Lebesgue covering dimension. For any topological space
X, we have
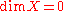if and only if 
Urysohn's theorem states that when X is a normal space
with a countable base, then
.
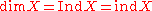Such spaces are exactly the separable and metrizable X (see Urysohn's metrization theorem).
The Nöbeling-Pontryagin theorem then states that such spaces with finite dimension are characterised up to homeomorphism as the subspaces of the Euclidean space
s, with their usual topology. The Menger-Nöbeling theorem (1932) states that if X is compact metric separable and of dimension n, then it embeds as a subspace of Euclidean space of dimension 2n + 1. (Georg Nöbeling
was a student of Karl Menger
. He introduced Nöbeling space, the subspace of R2n + 1 consisting of points with at least n + 1 co-ordinates being irrational number
s, which has universal properties for embedding spaces of dimension n.)
Assuming only X metrizable we have (Miroslav Katětov
)
or assuming X compact
and Hausdorff
(P. S. Aleksandrov)
Either inequality here may be strict; an example of Vladimir V. Filippov shows that the two inductive dimensions may differ.
A separable metric space X satisfies the inequality
if and only if for every closed sub-space 
of the space 
and each continuous mapping 
there exists a continuous extension 
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the inductive dimension of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is either of two values, the small inductive dimension ind(X) or the large inductive dimension Ind(X). These are based on the observation that, in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, (n − 1)-dimensional sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s (that is, the boundaries
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of n-dimensional balls) have dimension n − 1. Therefore it should be possible to define the dimension of a space inductively
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
in terms of the dimensions of the boundaries of suitable open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s.
The small and large inductive dimensions are two of the three most usual ways of capturing the notion of "dimension" for a topological space, in a way that depends only on the topology (and not, say, on the properties of a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
). The other is the Lebesgue covering dimension
Lebesgue covering dimension
Lebesgue covering dimension or topological dimension is one of several inequivalent notions of assigning a topological invariant dimension to a given topological space.-Definition:...
. The term "topological dimension" is ordinarily understood to refer to Lebesgue covering dimension. For "sufficiently nice" spaces, the three measures of dimension are equal.
Formal definition
We want the dimension of a point to be 0, and a point has empty boundary, so we start withThen inductively, ind(X) is the smallest n such that, for every
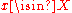and every open set U containing x, there is an open V containing x, where the closureClosure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of V is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of U, such that the boundary of V has small inductive dimension less than or equal to n − 1. (In the case above, where X is Euclidean n-dimensional space, V will be chosen to be an n-dimensional ball centered at x.)
For the large inductive dimension, we restrict the choice of V still further; Ind(X) is the smallest n such that, for every closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subset F of every open subset U of X, there is an open V in between (that is, F is a subset of V and the closure of V is a subset of U), such that the boundary of V has large inductive dimension less than or equal to n − 1.
Relationship between dimensions
Let be the Lebesgue covering dimension. For any topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, we have
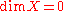if and only if Urysohn's theorem states that when X is a normal space
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
with a countable base, then
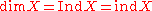.Such spaces are exactly the separable and metrizable X (see Urysohn's metrization theorem).
The Nöbeling-Pontryagin theorem then states that such spaces with finite dimension are characterised up to homeomorphism as the subspaces of the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s, with their usual topology. The Menger-Nöbeling theorem (1932) states that if X is compact metric separable and of dimension n, then it embeds as a subspace of Euclidean space of dimension 2n + 1. (Georg Nöbeling
Georg Nöbeling
Georg August Nöbeling was a German mathematician.Born and raised in Lüdenscheid, Nöbeling studied mathematics and physics in Göttingen and Vienna where he was a student of Karl Menger and received his PhD in 1931 on a generalization of the embedding theorem, which for one special case can be...
was a student of Karl Menger
Karl Menger
Karl Menger was a mathematician. He was the son of the famous economist Carl Menger. He is credited with Menger's theorem. He worked on mathematics of algebras, algebra of geometries, curve and dimension theory, etc...
. He introduced Nöbeling space, the subspace of R2n + 1 consisting of points with at least n + 1 co-ordinates being irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s, which has universal properties for embedding spaces of dimension n.)
Assuming only X metrizable we have (Miroslav Katětov
Miroslav Katetov
Miroslav Katětov |Chembar]], Russia – December 15, 1995) was a Czech mathematician, chess master, and psychologist. His research interests in mathematics included topology and functional analysis. He was an author of the Katětov–Tong insertion theorem. From 1953 to 1957 he was rector of Charles...
)
- ind X ≤ Ind X = dim X;
or assuming X compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(P. S. Aleksandrov)
- dim X ≤ ind X ≤ Ind X.
Either inequality here may be strict; an example of Vladimir V. Filippov shows that the two inductive dimensions may differ.
A separable metric space X satisfies the inequality
if and only if for every closed sub-space of the space and each continuous mapping there exists a continuous extension .Further reading
- Crilly, Tony, 2005, "Paul Urysohn and Karl Menger: papers on dimension theory" in Grattan-Guinness, I.Ivor Grattan-GuinnessIvor Grattan-Guinness, born 23 June 1941, in Bakewell, in England, is a historian of mathematics and logic.He gained his Bachelor degree as a Mathematics Scholar at Wadham College, Oxford, got an M.Sc in Mathematical Logic and the Philosophy of Science at the London School of Economics in 1966...
, ed., Landmark Writings in Western Mathematics. Elsevier: 844-55. - R. Engelking, Theory of Dimensions. Finite and Infinite, Heldermann Verlag (1995), ISBN 3-88538-010-2.
- V. V. Fedorchuk, The Fundamentals of Dimension Theory, appearing in Encyclopaedia of Mathematical Sciences, Volume 17, General Topology I, (1993) A. V. Arkhangel'skii and L. S. Pontryagin (Eds.), Springer-Verlag, Berlin ISBN 3-540-18178-4.
- V. V. Filippov, On the inductive dimension of the product of bicompacta, Soviet. Math. Dokl., 13 (1972), N° 1, 250-254.
- A. R. Pears, Dimension theory of general spaces, Cambridge University Press (1975).