Topological indistinguishability
Encyclopedia
In topology
, two points of a topological space
X are topologically indistinguishable if they have exactly the same neighborhoods. That is, if x and y are points in X, and A is the set of all neighborhoods that contain x, and B is the set of all neighborhoods that contain y, then x and y are "topologically indistinguishable" if and only if
A = B.
Intuitively, two points are topologically indistinguishable if the topology of X is unable to discern between the points.
Two points of X are topologically distinguishable if they are not topologically indistinguishable. This means there is an open set
containing precisely one of the two points (equivalently, there is a closed set
containing precisely one of the two points). This open set can then be used to distinguish between the two points. A T0 space is a topological space in which every pair of distinct points is topologically distinguishable. This is the weakest of the separation axiom
s.
Topological indistinguishability defines an equivalence relation
on any topological space X. If x and y are points of X we write x ≡ y for “x and y are topologically indistinguishable”. The equivalence class of x will be denoted by [x].
s) the notion of topological indistinguishability is trivial, so one must look to non-T0 spaces to find interesting examples. On the other hand, regularity
and normality
do not imply T0, so we can find examples with these properties. In fact, almost all of the examples given below are completely regular.
on X called the specialization preorder. For points x and y in X this preorder is defined by
where cl{y} denotes the closure
of {y}. Equivalently, x ≤ y if the neighborhood system of x, denoted Nx, is contained in the neighborhood system of y:
It is easy to see that this relation on X is reflexive
and transitive
and so defines a preorder. In general, however, this preorder will not be antisymmetric
. Indeed, the equivalence relation determined by ≤ is precisely that of topological indistinguishability:
A topological space is said to be symmetric (or R0) if the specialization preorder is symmetric
(i.e. x ≤ y implies y ≤ x). In this case, the relations ≤ and ≡ are identical. Topological indistinguishability is better behaved in these spaces and easier to understand. Note that this class of spaces includes all regular
and completely regular spaces.
s of x and y by cl{x} and cl{y}, and the respective neighborhood systems by Nx and Ny. Then the following statements are equivalent:
These conditions can be simplified in the case where X is symmetric space. For these spaces (in particular, for regular space
s), the following statements are equivalent:
and lower sets of x. These are both defined with respect to the specialization preorder discussed above.
The lower set of x is just the closure of {x}:
while the upper set of x is the intersection
of the neighborhood system at x:
The equivalence class of x is then given by the intersection
Since ↓x is the intersection of all the closed sets containing x and ↑x is the intersection of all the open sets containing x, the equivalence class [x] is the intersection of all the open and closed sets containing x.
Both cl{x} and ∩Nx will contain the equivalence class [x]. In general, both sets will contain additional points as well. In symmetric spaces (in particular, in regular space
s) however, the three sets coincide: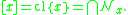
In general, the equivalence classes [x] will be closed if and only if the space is symmetric.
The converse is generally false (There are quotients
of T0 spaces which are trivial
). The converse will hold if X has the initial topology
induced by f. More generally, if X has the initial topology induced by a family of maps
then
It follows that two elements in a product space are topologically indistinguishable if and only if each of their components are topologically indistinguishable.
KX = X/≡. The space KX is called the Kolmogorov quotient or T0 identification of X. The space KX is, in fact, T0 (i.e. all points are topologically distinguishable). Moreover, by the characteristic property of the quotient map any continuous map f : X → Y from X to a T0 space factors through the quotient map q : X → KX.
Although the quotient map q is generally not a homeomorphism
(since it is not generally injective
), it does induce a bijection
between the topologies of X and the topologies of KX. Intuitively, the Kolmogorov quotient does not alter the topology of a space. It just reduces the point set until points become topologically distinguishable.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, two points of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X are topologically indistinguishable if they have exactly the same neighborhoods. That is, if x and y are points in X, and A is the set of all neighborhoods that contain x, and B is the set of all neighborhoods that contain y, then x and y are "topologically indistinguishable" if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
A = B.
Intuitively, two points are topologically indistinguishable if the topology of X is unable to discern between the points.
Two points of X are topologically distinguishable if they are not topologically indistinguishable. This means there is an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
containing precisely one of the two points (equivalently, there is a closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
containing precisely one of the two points). This open set can then be used to distinguish between the two points. A T0 space is a topological space in which every pair of distinct points is topologically distinguishable. This is the weakest of the separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s.
Topological indistinguishability defines an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on any topological space X. If x and y are points of X we write x ≡ y for “x and y are topologically indistinguishable”. The equivalence class of x will be denoted by [x].
Examples
For T0 spaces (in particular, for Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s) the notion of topological indistinguishability is trivial, so one must look to non-T0 spaces to find interesting examples. On the other hand, regularity
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
and normality
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
do not imply T0, so we can find examples with these properties. In fact, almost all of the examples given below are completely regular.
- In an indiscrete space, any two points are topologically indistinguishable.
- In a pseudometric spacePseudometric spaceIn mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
, two points are topologically indistinguishable if and only if the distance between them is zero. - In a seminormed vector space, x ≡ y if and only if ‖x − y‖ = 0.
- For example, let L2(R) be the space of all measurable functionMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s from R to R which are square integrable (see Lp spaceLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
). Then two functions f and g in L2(R) are topologically indistinguishable if and only if they are equal almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
.
- For example, let L2(R) be the space of all measurable function
- In a topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, x ≡ y if and only if x−1y ∈ cl{e} where cl{e} is the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the trivial subgroup. The equivalence classes are just the cosetCosetIn mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of cl{e} (which is always a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
). - Uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s generalize both pseudometric spaces and topological groups. In a uniform space, x ≡ y if and only if the pair (x, y) belongs to every entourage. The intersection of all the entourages is an equivalence relation on X which is just that of topological indistinguishability. - Let X have the initial topologyInitial topologyIn general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
with respect to a family of functions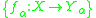
. Then two points x and y in X will be topologically indistinguishable if the family 
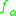does not separate them (i.e. 
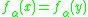for all 
). - Given any equivalence relation on a set X there is a topology on X for which the notion of topological indistinguishability agrees with the given equivalence relation. One can simply take the equivalence classes as a baseBase (topology)In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for the topology. This is called the partition topologyPartition topologyIn mathematics, the partition topology is a topology that can be induced on any set X by partitioning X into disjoint subsets P; these subsets form the basis for the topology...
on X.
Specialization preorder
The topological indistinguishability relation on a space X can be recovered from a natural preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
on X called the specialization preorder. For points x and y in X this preorder is defined by
- x ≤ y if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
x ∈ cl{y}
where cl{y} denotes the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of {y}. Equivalently, x ≤ y if the neighborhood system of x, denoted Nx, is contained in the neighborhood system of y:
- x ≤ y if and only if Nx ⊂ Ny.
It is easy to see that this relation on X is reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
and so defines a preorder. In general, however, this preorder will not be antisymmetric
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
. Indeed, the equivalence relation determined by ≤ is precisely that of topological indistinguishability:
- x ≡ y if and only if x ≤ y and y ≤ x.
A topological space is said to be symmetric (or R0) if the specialization preorder is symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
(i.e. x ≤ y implies y ≤ x). In this case, the relations ≤ and ≡ are identical. Topological indistinguishability is better behaved in these spaces and easier to understand. Note that this class of spaces includes all regular
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
and completely regular spaces.
Equivalent conditions
There are several equivalent ways of determining when two points are topologically indistinguishable. Let X be a topological space and let x and y be points of X. Denote the respective closureClosure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
s of x and y by cl{x} and cl{y}, and the respective neighborhood systems by Nx and Ny. Then the following statements are equivalent:
- x ≡ y
- for each open set U in X, either U contains both x and y or neither of them
- Nx = Ny
- x ∈ cl{y} and y ∈ cl{x}
- cl{x} = cl{y}
- x ∈ ∩Ny and y ∈ ∩Nx
- ∩Nx = ∩Ny
- x ∈ cl{y} and x ∈ ∩Ny
- x belongs to every open set and every closed set containing y
- a net or filter converges to x if and only if it converges to y
These conditions can be simplified in the case where X is symmetric space. For these spaces (in particular, for regular space
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
s), the following statements are equivalent:
- x ≡ y
- for each open set U, if x ∈ U then y ∈ U
- Nx ⊂ Ny
- x ∈ cl{y}
- x ∈ ∩Ny
- x belongs to every closed set containing y
- x belongs to every open set containing y
- every net or filter that converges to x converges to y
Equivalence classes
To discuss the equivalence class of x, it is convenient to first define the upperUpper set
In mathematics, an upper set of a partially ordered set is a subset U with the property that x is in U and x≤y imply y is in U....
and lower sets of x. These are both defined with respect to the specialization preorder discussed above.
The lower set of x is just the closure of {x}:
while the upper set of x is the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the neighborhood system at x:
The equivalence class of x is then given by the intersection
Since ↓x is the intersection of all the closed sets containing x and ↑x is the intersection of all the open sets containing x, the equivalence class [x] is the intersection of all the open and closed sets containing x.
Both cl{x} and ∩Nx will contain the equivalence class [x]. In general, both sets will contain additional points as well. In symmetric spaces (in particular, in regular space
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
s) however, the three sets coincide:
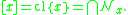
In general, the equivalence classes [x] will be closed if and only if the space is symmetric.
Continuous functions
Let f : X → Y be a continuous function. Then for any x and y in X- x ≡ y implies f(x) ≡ f(y).
The converse is generally false (There are quotients
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of T0 spaces which are trivial
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
). The converse will hold if X has the initial topology
Initial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
induced by f. More generally, if X has the initial topology induced by a family of maps
then
- x ≡ y if and only if fα(x) ≡ fα(y) for all α.
It follows that two elements in a product space are topologically indistinguishable if and only if each of their components are topologically indistinguishable.
Kolmogorov quotient
Since topological indistinguishability is an equivalence relation on any topological space X, we can form the quotient spaceQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
KX = X/≡. The space KX is called the Kolmogorov quotient or T0 identification of X. The space KX is, in fact, T0 (i.e. all points are topologically distinguishable). Moreover, by the characteristic property of the quotient map any continuous map f : X → Y from X to a T0 space factors through the quotient map q : X → KX.
Although the quotient map q is generally not a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
(since it is not generally injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
), it does induce a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the topologies of X and the topologies of KX. Intuitively, the Kolmogorov quotient does not alter the topology of a space. It just reduces the point set until points become topologically distinguishable.