In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a limaçon trisectrix (called simply a trisectrix by some authors) is a member of the Limaçon

Limaçon

In geometry, a limaçon or limacon , also known as a limaçon of Pascal, is defined as a roulette formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller...

 family of curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

s which has the trisectrix

Trisectrix

In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...

, or angle trisection

Angle trisection

Angle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass....

, property. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 2:3 and the lines initially coincide with the line between the two points. Thus, it is an example of a sectrix of Maclaurin

Sectrix of Maclaurin

In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is...

.

Equations

If the first line is rotating about the origin forms angle θ with the x-axis, and the second line is rotating about the point (a, 0) has angle 3θ/2, then the angle between them is θ/2 and the law of sines

Law of sines

In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...

 can be used to determine the distance from the point of intersection to the origin as.
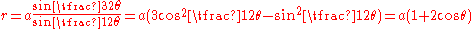This is the equation polar coordinates

Polar coordinate system

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....

 and shows the curve is a Limaçon. The curve crosses itself at the origin, the rightmost point of the outer loop is at (3a, 0) and the tip of the inner loop is at (a, 0).

If the curve is shifted so that the origin is at the tip of the inner loop then the equation becomes
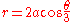
so it is also in the rose

Rose (mathematics)

In mathematics, a rose or rhodonea curve is a sinusoid plotted in polar coordinates. Up to similarity, thesecurves can all be expressed by a polar equation of the form\!\,r=\cos.If k is an integer, the curve will be rose shaped with...

family of curves.

The trisection property

There are several ways to use the curve to trisect an angle. Let φ be the angle to be trisected. First, draw a ray from the tip of the small loop at (a, 0) with angle φ with the x-axis. Let P be the point where the ray intersects the curve, assumed to be on the outer loop if φ is small. Draw another ray from the origin to P. Then the angle between to two rays at P trisects φ. This follows easily from the construction of the curve given above.

For the second method, draw a circle of radius a and center at the origin. Draw a ray from the origin with angle φ with the x-axis. Let S be the point where this ray intersects the circle and draw the line from S to (a, 0). Let J be the point there this line intersects the curve, assumed to be on the inner loop if φ is small. The line from the origin to J has angle φ/3 with the x-axis.

By rotating the curve, the second form of the equation becomes.
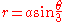So if a right triangle is constructed with side r and hypotenuse a then the angle between them will be θ/3. It is straightforward to generate a third method from this.