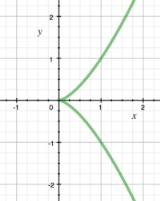
Singular point of a curve
Overview
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a singular point on a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
is one where the curve is not given by a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.
Algebraic curves in the plane may be defined as the set of points (x, y) satisfying an equation of the form f(x, y)=0, where f is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function f:R2→R.

