
Limit ordinal
Encyclopedia
A limit ordinal is an ordinal number
which is neither zero nor a successor ordinal
.
Various equivalent ways to express this are:
Some contention exists on whether or not 0 should be classified as a limit ordinal, as it does not have an immediate predecessor;
some textbooks include 0 in the class of limit ordinals while others exclude it.
of ordinal numbers is well-order
ed, there is a smallest infinite limit ordinal; denoted by ω. This ordinal ω is also the smallest infinite ordinal (disregarding limit), as it is the least upper bound of the natural numbers. Hence ω represents the order type of the natural numbers. The next limit ordinal above the first is ω + ω = ω·2, and then we have ω·n, for any natural number n. Taking the union
(the supremum
operation on any set of ordinals) of all the ω·n, we get ω·ω = ω2. This process can be iterated as follows to produce:

In general, all of these recursive definitions via multiplication, exponentiation, repeated exponentiation, etc. yield limit ordinals. All of the ordinals discussed so far are still countable ordinals. However, there is no recursively enumerable scheme for systematically naming
all ordinals less than the Church–Kleene ordinal which is a countable ordinal.
Beyond the countable, the first uncountable ordinal
is usually denoted ω1. It is also a limit ordinal.
Continuing, one can obtain the following (all of which are now increasing in cardinality):
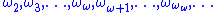
In general, we always get a limit ordinal when taking the union of a set of ordinals that has no maximum element.
The ordinals of the form ω²α, for α > 0, are limits of limits, etc.
or definitions by transfinite recursion. Limit ordinals represent a sort of "turning point" in such procedures, in which one must use limiting operations such as taking the union over all preceding ordinals. In principle, one could do anything at limit ordinals, but taking the union is continuous in the order topology and this is usually desirable.
If we use the Von Neumann cardinal assignment
, every infinite cardinal number
is also a limit ordinal (and this is a fitting observation, as cardinal derives from the Latin cardo meaning hinge or turning point): the proof of this fact is done by simply showing that every infinite successor ordinal is equinumerous to a limit ordinal via the Hotel Infinity
argument.
Cardinal numbers have their own notion of successorship and limit (everything getting upgraded to a higher level).
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
which is neither zero nor a successor ordinal
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
.
Various equivalent ways to express this are:
- It cannot be reached via the ordinal successor operationSuccessor ordinalIn set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
S; in precise terms, we say λ is a limit ordinal if and only if λ > 0 and for any β < λ, there exists γ such that β < γ < λ. - It is equal to the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of all the ordinals below it, but is not zero. (Compare with a successor ordinal: the set of ordinals below it has a maximum, so the supremum is this maximum, the previous ordinal.) - It is not zero and has no maximum element.
- It can be written in the form ωα for α > 0. That is, in the Cantor normal form there is no finite number as last term, and the ordinal is nonzero.
- It is a limit pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of the class of ordinal numbers, with respect to the order topologyOrder topologyIn mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
. (The other ordinals are isolated pointIsolated pointIn topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s.)
Some contention exists on whether or not 0 should be classified as a limit ordinal, as it does not have an immediate predecessor;
some textbooks include 0 in the class of limit ordinals while others exclude it.
Examples
Because the classClass (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of ordinal numbers is well-order
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
ed, there is a smallest infinite limit ordinal; denoted by ω. This ordinal ω is also the smallest infinite ordinal (disregarding limit), as it is the least upper bound of the natural numbers. Hence ω represents the order type of the natural numbers. The next limit ordinal above the first is ω + ω = ω·2, and then we have ω·n, for any natural number n. Taking the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
(the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
operation on any set of ordinals) of all the ω·n, we get ω·ω = ω2. This process can be iterated as follows to produce:

In general, all of these recursive definitions via multiplication, exponentiation, repeated exponentiation, etc. yield limit ordinals. All of the ordinals discussed so far are still countable ordinals. However, there is no recursively enumerable scheme for systematically naming
Ordinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
all ordinals less than the Church–Kleene ordinal which is a countable ordinal.
Beyond the countable, the first uncountable ordinal
First uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
is usually denoted ω1. It is also a limit ordinal.
Continuing, one can obtain the following (all of which are now increasing in cardinality):
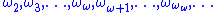
In general, we always get a limit ordinal when taking the union of a set of ordinals that has no maximum element.
The ordinals of the form ω²α, for α > 0, are limits of limits, etc.
Properties
The classes of successor ordinals and limit ordinals (of various cofinalities) as well as zero exhaust the entire class of ordinals, so these cases are often used in proofs by transfinite inductionTransfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
or definitions by transfinite recursion. Limit ordinals represent a sort of "turning point" in such procedures, in which one must use limiting operations such as taking the union over all preceding ordinals. In principle, one could do anything at limit ordinals, but taking the union is continuous in the order topology and this is usually desirable.
If we use the Von Neumann cardinal assignment
Von Neumann cardinal assignment
The von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:...
, every infinite cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
is also a limit ordinal (and this is a fitting observation, as cardinal derives from the Latin cardo meaning hinge or turning point): the proof of this fact is done by simply showing that every infinite successor ordinal is equinumerous to a limit ordinal via the Hotel Infinity
Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...
argument.
Cardinal numbers have their own notion of successorship and limit (everything getting upgraded to a higher level).

