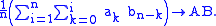Cauchy product
Encyclopedia
In mathematics
, the Cauchy product, named after Augustin Louis Cauchy
, of two sequence
s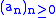 ,
, 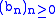 , is the discrete convolution
, is the discrete convolution
of the two sequences, the sequence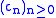 whose general term is given by
whose general term is given by
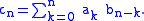
In other words, it is the sequence whose associated formal power series
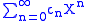 is the product of the two series similarly associated to
is the product of the two series similarly associated to 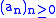 and
and 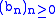 .
.
 to be terms of two strictly formal (not necessarily convergent) series
to be terms of two strictly formal (not necessarily convergent) series

usually, of real
or complex
numbers. Then the Cauchy product is defined by a discrete convolution
as follows.
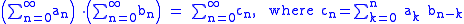
for n = 0, 1, 2, ...
"Formal" means we are manipulating series in disregard of any questions of convergence. These need not be convergent series. See in particular formal power series
.
One hopes, by analogy with finite sums, that in cases in which the two series do actually converge, the sum of the infinite series
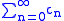
is equal to the product

just as would work when each of the two sums being multiplied has only finitely many terms.
This is not true in general, but see Mertens' Theorem and Cesàro's theorem below for some special cases.
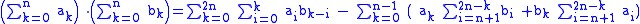
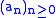 and
and 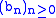 be real sequences. It was proved by Franz Mertens
be real sequences. It was proved by Franz Mertens
that if the series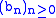 converges to B and the series
converges to B and the series 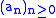 converges absolutely
converges absolutely
to A then their Cauchy product converges to AB. It is not sufficient for both series to be conditionally convergent. For example, the sequences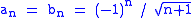 are conditionally convergent but their Cauchy product does not converge.
are conditionally convergent but their Cauchy product does not converge.
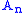 ,
, 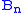 and
and  denote the partial sums
denote the partial sums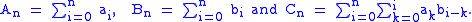
Then
by rearrangement. So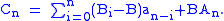
Fix ε > 0. Since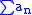 is absolutely convergent and
is absolutely convergent and  is convergent then there exists an integer N such that for all
is convergent then there exists an integer N such that for all  we have
we have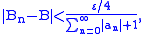
and an integer M such that for all it holds that
it holds that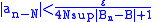
(since the series converges, the sequence must converge to 0). Also, there exists an integer L such that if then
then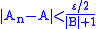 .
.
Therefore for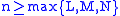 we have
we have
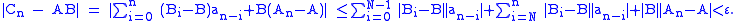
By the definition of convergence of a series as required.
as required.
 for all
for all 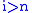 and
and  for all
for all  . Here the Cauchy product of
. Here the Cauchy product of  and
and  is readily verified to be
is readily verified to be 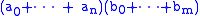 . Therefore, for finite series (which are finite sums), Cauchy multiplication is direct multiplication of those series.
. Therefore, for finite series (which are finite sums), Cauchy multiplication is direct multiplication of those series.
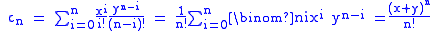
by definition and the binomial formula. Since, formally,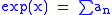 and
and 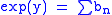 , we have shown that
, we have shown that  . Since the limit of the Cauchy product of two absolutely convergent
. Since the limit of the Cauchy product of two absolutely convergent
series is equal to the product of the limits of those series, we have proven the formula for all
for all  .
.
. Specifically:
If ,
, 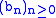 are real sequences with
are real sequences with  and
and 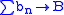 then
then
This can be generalised to the case where the two sequences are not convergent but just Cesàro summable:
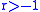 and
and  , suppose the sequence
, suppose the sequence  is
is  summable with sum A and
summable with sum A and 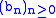 is
is  summable with sum B. Then their Cauchy product is
summable with sum B. Then their Cauchy product is 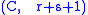 summable with sum AB.
summable with sum AB.
 (complex number
(complex number
s). The Cauchy product can be defined for series in the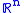 spaces (Euclidean spaces) where multiplication is the inner product. In this case, we have the result that if two series converge absolutely then their Cauchy product converges absolutely to the inner product of the limits.
spaces (Euclidean spaces) where multiplication is the inner product. In this case, we have the result that if two series converge absolutely then their Cauchy product converges absolutely to the inner product of the limits.
 . In this case the Cauchy product is not always defined: for instance, the Cauchy product of the constant sequence 1 with itself,
. In this case the Cauchy product is not always defined: for instance, the Cauchy product of the constant sequence 1 with itself, 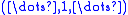 is not defined. This doesn't arise for singly infinite sequences, as these have only finite sums.
is not defined. This doesn't arise for singly infinite sequences, as these have only finite sums.
One has some pairings, for instance the product of a finite sequence with any sequence, and the product .
.
This is related to duality of Lp spaces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cauchy product, named after Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
, of two sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s
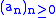 ,
, 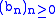 , is the discrete convolution
, is the discrete convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the two sequences, the sequence
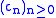 whose general term is given by
whose general term is given by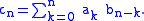
In other words, it is the sequence whose associated formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
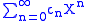 is the product of the two series similarly associated to
is the product of the two series similarly associated to 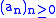 and
and 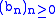 .
.Series
A particularly important example is to consider the sequences to be terms of two strictly formal (not necessarily convergent) series
to be terms of two strictly formal (not necessarily convergent) seriesSeries (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....

usually, of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers. Then the Cauchy product is defined by a discrete convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
as follows.
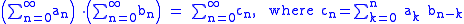
for n = 0, 1, 2, ...
"Formal" means we are manipulating series in disregard of any questions of convergence. These need not be convergent series. See in particular formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
.
One hopes, by analogy with finite sums, that in cases in which the two series do actually converge, the sum of the infinite series
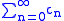
is equal to the product

just as would work when each of the two sums being multiplied has only finitely many terms.
This is not true in general, but see Mertens' Theorem and Cesàro's theorem below for some special cases.
Finite summations
The product of two finite series ak and bk with k between 0 and 2n satisfies the equation: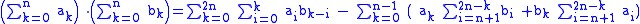
Convergence and Mertens' theorem
Let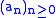 and
and 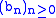 be real sequences. It was proved by Franz Mertens
be real sequences. It was proved by Franz MertensFranz Mertens
Franz Mertens was a German mathematician. He was born in Środa in the Grand Duchy of Poznań, Kingdom of Prussia and died in Vienna, Austria....
that if the series
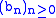 converges to B and the series
converges to B and the series 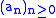 converges absolutely
converges absolutelyAbsolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
to A then their Cauchy product converges to AB. It is not sufficient for both series to be conditionally convergent. For example, the sequences
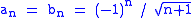 are conditionally convergent but their Cauchy product does not converge.
are conditionally convergent but their Cauchy product does not converge.Proof of Mertens' theorem
Let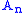 ,
, 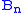 and
and  denote the partial sums
denote the partial sums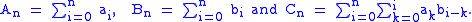
Then

by rearrangement. So
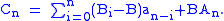
Fix ε > 0. Since
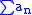 is absolutely convergent and
is absolutely convergent and  is convergent then there exists an integer N such that for all
is convergent then there exists an integer N such that for all  we have
we have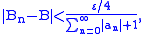
and an integer M such that for all
 it holds that
it holds that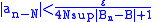
(since the series converges, the sequence must converge to 0). Also, there exists an integer L such that if
 then
then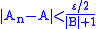 .
.Therefore for
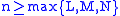 we have
we have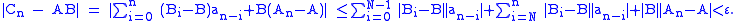
By the definition of convergence of a series
 as required.
as required.Finite series
Suppose for all
for all 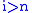 and
and  for all
for all  . Here the Cauchy product of
. Here the Cauchy product of  and
and  is readily verified to be
is readily verified to be 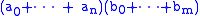 . Therefore, for finite series (which are finite sums), Cauchy multiplication is direct multiplication of those series.
. Therefore, for finite series (which are finite sums), Cauchy multiplication is direct multiplication of those series.Infinite series
- For some
 , let
, let 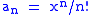 and
and 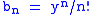 . Then
. Then
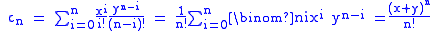
by definition and the binomial formula. Since, formally,
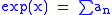 and
and 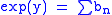 , we have shown that
, we have shown that  . Since the limit of the Cauchy product of two absolutely convergent
. Since the limit of the Cauchy product of two absolutely convergentAbsolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
series is equal to the product of the limits of those series, we have proven the formula
 for all
for all  .
.- As a second example, let
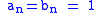 for all
for all  . Then
. Then  for all
for all  so the Cauchy product
so the Cauchy product 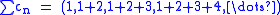 does not converge.
does not converge.
Cesàro's theorem
In cases where the two sequences are convergent but not absolutely convergent, the Cauchy product is still Cesàro summableCesàro summation
In mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
. Specifically:
If
 ,
, 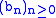 are real sequences with
are real sequences with  and
and 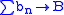 then
thenThis can be generalised to the case where the two sequences are not convergent but just Cesàro summable:
Theorem
For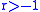 and
and  , suppose the sequence
, suppose the sequence  is
is  summable with sum A and
summable with sum A and 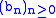 is
is  summable with sum B. Then their Cauchy product is
summable with sum B. Then their Cauchy product is 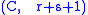 summable with sum AB.
summable with sum AB.Generalizations
All of the foregoing applies to sequences in (complex number
(complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s). The Cauchy product can be defined for series in the
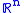 spaces (Euclidean spaces) where multiplication is the inner product. In this case, we have the result that if two series converge absolutely then their Cauchy product converges absolutely to the inner product of the limits.
spaces (Euclidean spaces) where multiplication is the inner product. In this case, we have the result that if two series converge absolutely then their Cauchy product converges absolutely to the inner product of the limits.Relation to convolution of functions
One can also define the Cauchy product of doubly infinite sequences, thought of as functions on . In this case the Cauchy product is not always defined: for instance, the Cauchy product of the constant sequence 1 with itself,
. In this case the Cauchy product is not always defined: for instance, the Cauchy product of the constant sequence 1 with itself, 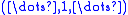 is not defined. This doesn't arise for singly infinite sequences, as these have only finite sums.
is not defined. This doesn't arise for singly infinite sequences, as these have only finite sums.One has some pairings, for instance the product of a finite sequence with any sequence, and the product
 .
.This is related to duality of Lp spaces.