Free semigroup
Encyclopedia
In abstract algebra
, the free monoid on a set A is the monoid
whose elements are all the finite sequences (or strings) of zero or more elements from A. It is usually denoted A∗. The identity element
is the unique sequence of zero elements, often called the empty string
and denoted by ε or λ, and the monoid operation is string concatenation. The free semigroup
on A is the subsemigroup of A∗ containing all elements except the empty string. It is usually denoted A+.
More generally, an abstract monoid (or semigroup) S is described as free if it is isomorphic to the free monoid (or semigroup) on some set.
As the name implies, free monoids and semigroups are those objects which satisfy the usual universal property
defining free object
s, in the respective categories
of monoids and semigroups. It follows that every monoid (or semigroup) arises as a homomorphic image of a free monoid (or semigroup). The study of semigroups as images of free semigroups is called combinatorial semigroup theory.
. More generally, if S is an abstract free monoid (semigroup), then a set of elements which maps onto the set of single-letter words under an isomorphism to a semigroup A+ (monoid A∗) is called a set of free generators for S.
Each free semigroup (or monoid) S has exactly one set of free generators, the cardinality of which is called the rank of S.
Two free monoids or semigroups are isomorphic if and only if they have the same rank. In fact, every set of generators for a free semigroup or monoid S contains the free generators. It follows that a free semigroup or monoid is finitely generated if and only if it has finite rank.
If Σ is a finite alphabet (a set of symbols), then Σ∗ consists of all words over Σ in the sense of formal language
theory. Thus, the abstract study of formal languages can be thought of as the study of subsets of finitely generated free monoids. There are deep connections between the theory of semigroups and that of automata
. For example, the regular language
s over Σ are the homomorphic pre-images in Σ∗ of subsets of finite monoids.
For example, if A = {a, b, c} elements of A∗ are of the form
If A is a set, the word length function on A∗ is the unique monoid homomorphism from A∗ to N that maps each element of A to 1.
. That is, given a letter a ∈ Σ and a string s ∈ Σ∗, define the string projection pa(s) by
Note that string projection is well-defined even if the rank of the monoid is infinite, as the above recursive definition works for all strings of finite length. String projection is a morphism
in the category of free monoids, so that
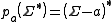
where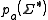
is understood to be the free monoid of all finite strings that don't contain the letter a. The identity morphism is 
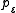, as clearly 
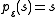for all strings s. Of course, it commutes with the operation of string concatenation, so that 
for all strings s and t. There are many right inverses to string projection, and thus it is a split epimorphism.
String projection is commutative, as clearly
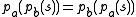
For free monoids of finite rank, this follows from the fact that free monoids of the same rank are isomorphic, as projection reduces the rank of the monoid by one.
String projection is idempotent, as
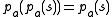
for all strings s. Thus, projection is an idempotent, commutative operation, and so it forms a bounded semilattice
or a commutative band
.
s with elements drawn from A, with the monoid operation being multiset sum and the monoid unit being the empty multiset.
For example, if A = {a, b, c}, elements of the free commutative monoid on A are of the form
The fundamental theorem of arithmetic
states that the monoid of positive integers under multiplication is a free commutative monoid on an infinite set of generators, the prime number
s.
The free commutative semigroup is the subset of the free commutative monoid which contains all multisets with elements drawn from A except the empty multiset.
, is a generalization that encompasses both the free and free commutative monoids as instances. This generalization finds applications in combinatorics
and in the study of parallelism
in computer science
.
where e is the identity on M. Computationally, every such homomorphism corresponds to a map
operation applying f to all the elements of a list, followed by a fold
operation which combines the results using the binary operator •. This computational paradigm (which can be generalised to non-associative binary operators) has inspired the MapReduce
software framework.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the free monoid on a set A is the monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
whose elements are all the finite sequences (or strings) of zero or more elements from A. It is usually denoted A∗. The identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
is the unique sequence of zero elements, often called the empty string
Empty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
and denoted by ε or λ, and the monoid operation is string concatenation. The free semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
on A is the subsemigroup of A∗ containing all elements except the empty string. It is usually denoted A+.
More generally, an abstract monoid (or semigroup) S is described as free if it is isomorphic to the free monoid (or semigroup) on some set.
As the name implies, free monoids and semigroups are those objects which satisfy the usual universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
defining free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
s, in the respective categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of monoids and semigroups. It follows that every monoid (or semigroup) arises as a homomorphic image of a free monoid (or semigroup). The study of semigroups as images of free semigroups is called combinatorial semigroup theory.
Free generators and rank
The members of a set A are called the free generators for A∗ and A+. The superscript * is then commonly understood to be the Kleene starKleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
. More generally, if S is an abstract free monoid (semigroup), then a set of elements which maps onto the set of single-letter words under an isomorphism to a semigroup A+ (monoid A∗) is called a set of free generators for S.
Each free semigroup (or monoid) S has exactly one set of free generators, the cardinality of which is called the rank of S.
Two free monoids or semigroups are isomorphic if and only if they have the same rank. In fact, every set of generators for a free semigroup or monoid S contains the free generators. It follows that a free semigroup or monoid is finitely generated if and only if it has finite rank.
Examples
The monoid (N,+) of natural numbers (including zero) under addition is a free monoid on a single generator (i.e. rank 1). The unique free generator is the number 1.If Σ is a finite alphabet (a set of symbols), then Σ∗ consists of all words over Σ in the sense of formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory. Thus, the abstract study of formal languages can be thought of as the study of subsets of finitely generated free monoids. There are deep connections between the theory of semigroups and that of automata
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
. For example, the regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s over Σ are the homomorphic pre-images in Σ∗ of subsets of finite monoids.
For example, if A = {a, b, c} elements of A∗ are of the form
- {ε, a, ab, ba, caa, cccbabbc,...}
If A is a set, the word length function on A∗ is the unique monoid homomorphism from A∗ to N that maps each element of A to 1.
String projection
The operation of string projection is an endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
. That is, given a letter a ∈ Σ and a string s ∈ Σ∗, define the string projection pa(s) by
Note that string projection is well-defined even if the rank of the monoid is infinite, as the above recursive definition works for all strings of finite length. String projection is a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
in the category of free monoids, so that
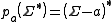
where
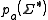is understood to be the free monoid of all finite strings that don't contain the letter a. The identity morphism is 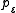, as clearly 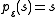for all strings s. Of course, it commutes with the operation of string concatenation, so that for all strings s and t. There are many right inverses to string projection, and thus it is a split epimorphism.String projection is commutative, as clearly
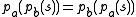
For free monoids of finite rank, this follows from the fact that free monoids of the same rank are isomorphic, as projection reduces the rank of the monoid by one.
String projection is idempotent, as
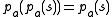
for all strings s. Thus, projection is an idempotent, commutative operation, and so it forms a bounded semilattice
Semilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
or a commutative band
Band (algebra)
In mathematics, a band is a semigroup in which every element is idempotent . Bands were first studied and named by ; the lattice of varieties of bands was described independently in the early 1970s by Biryukov, Fennemore and Gerhard...
.
The free commutative monoid
Given a set A, the free commutative monoid on A is the set of all finite multisetMultiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s with elements drawn from A, with the monoid operation being multiset sum and the monoid unit being the empty multiset.
For example, if A = {a, b, c}, elements of the free commutative monoid on A are of the form
- {ε, a, ab, a2b, ab3c4, ...}
The fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
states that the monoid of positive integers under multiplication is a free commutative monoid on an infinite set of generators, the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s.
The free commutative semigroup is the subset of the free commutative monoid which contains all multisets with elements drawn from A except the empty multiset.
Generalization
The free partially commutative monoid, or trace monoidTrace monoid
In mathematics and computer science, a trace is a set of strings, wherein certain letters in the string are allowed to commute, but others are not. It generalizes the concept of a string, by not forcing the letters to always be in a fixed order, but allowing certain reshufflings to take place...
, is a generalization that encompasses both the free and free commutative monoids as instances. This generalization finds applications in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and in the study of parallelism
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
Free monoids and computing
The free monoid on a set A corresponds to lists of elements from A with concatenation as the binary operation. A monoid homomorphism from the free monoid to any other monoid (M,•) is a function f such that- f(x1…xn) = f(x1) • … • f(xn)
- f = e
where e is the identity on M. Computationally, every such homomorphism corresponds to a map
Map (higher-order function)
In many programming languages, map is the name of a higher-order function that applies a given function to each element of a list, returning a list of results. They are examples of both catamorphisms and anamorphisms...
operation applying f to all the elements of a list, followed by a fold
Fold (higher-order function)
In functional programming, fold – also known variously as reduce, accumulate, compress, or inject – are a family of higher-order functions that analyze a recursive data structure and recombine through use of a given combining operation the results of recursively processing its...
operation which combines the results using the binary operator •. This computational paradigm (which can be generalised to non-associative binary operators) has inspired the MapReduce
MapReduce
MapReduce is a software framework introduced by Google in 2004 to support distributed computing on large data sets on clusters of computers. Parts of the framework are patented in some countries....
software framework.