Misiurewicz point
Encyclopedia
A Misiurewicz point is a parameter in the Mandelbrot set
(the parameter space
of quadratic polynomials) for which the critical point
is strictly preperiodic (i.e., it becomes periodic after finitely many iterations but is not periodic itself). By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set
where the unique critical point is strictly preperiodic. (This term makes less sense for maps in greater generality that have more than one (free) critical point because some critical points might be periodic and others not.)
is a Misiurewicz point 
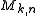if it satisfies the equations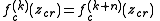
and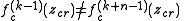
so :
where :
and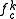
denotes the 
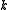-th iterate of 
.
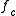Michał Misiurewicz
.
Note that the term "Misiurewicz point" is used ambiguously: Misiurewicz originally investigated maps in which all critical points were non-recurrent (that is, there is a neighborhood of every critical point that is not visited by the orbit of this critical point), and this meaning is firmly established in the context of dynamics of iterated interval maps. The case that for a quadratic polynomial the unique critical point is strictly preperiodic is only a very special case; in this restricted sense (as described above) this term is used in complex dynamics; a more appropriate term would be Misiurewicz-Thurston points (after William Thurston
who investigated postcritically finite rational maps).
Quadratic maps=
A complex quadratic polynomial
has only one critical point. By a suitable conjugation
any quadratic polynomial can be transformed into a map of the form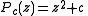
which has a single critical point at 
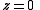. The Misiurewicz points of this family of maps are roots of the equations
,
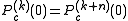(subject to the condition that the critical point is not periodic),
where :
For example, the Misiurewicz points with k=2 and n=1, denoted by M2,1, are roots of
.
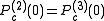
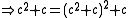
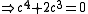The root c=0 is not a Misiurewicz point because the critical point is a fixed point
when c=0, and so is periodic rather than pre-periodic. This leaves a single Misiurewicz point M2,1 at c = −2.
of the Mandelbrot set
. Misiurewicz points are dense
in the boundary
of the Mandelbrot set
.
If
is a Misiurewicz point, then the associated filled Julia set
is equal to the Julia set
, and means the filled Julia set
has no interior
.
If
is a Misiurewicz point, then in the corresponding Julia set all periodic cycles are repelling (in particular the cycle that the critical orbit falls onto).
Mandelbrot set
and Julia set
are locally asymptotically similar
around Misiurewicz points. Mandelbrot set
is self-similar
around Misiurewicz points
According to the Branch Theorem of the Mandelbrot set, all branch points of the Mandelbrot set are Misiurewicz points (plus, in a combinatorial sense, hyperbolic components represented by their centers).
Many (actually, most) Misiurewicz parameters in the Mandelbrot set look like `centers of spirals'. The explanation for this is the following: at a Misiurewicz parameter, the critical value jumps onto a repelling periodic cycle after finitely many iterations; at each point on the cycle, the Julia set is asymptotically self-similar by a complex multiplication by the derivative of this cycle. If the derivative is non-real, then this implies that the Julia set, near the periodic cycle, has a spiral structure. A similar spiral structure thus occurs in the Julia set near the critical value and, by Tan Lei's aforementioned theorem, also in the Mandelbrot set near any Misiurewicz parameter for which the repelling orbit has non-real multiplier. Depending on the value of the multiplier, the spiral shape can seem more or less pronounced. The number of the arms at the spiral equals the number of branches at the Misiurewicz parameter, and this equals the number of branches at the critical value in the Julia set. (Even the `principal Misiurewicz point in the 1/3-limb', at the end of the parameter rays at angles 9/56, 11/56, and 15/56, turns out to be asymptotically a spiral, with infinitely many turns, even though this is hard to see without maginification.)
of Misiurewicz points, measured in turns
are :
where :
a and b are positive integers and b is odd ,
subscript number shows base of numeral system
.
Point 
:
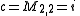Point
Notice that it is z-plane (dynamical plane
) not c-plane (parameter plane
) and point
is not the same point as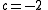 
.
Point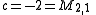
is landing point of only one external ray
( parameter ray) of angle 1/2 .
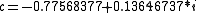is near a Misiurewicz point 
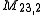. It is
Point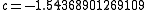
is near a Misiurewicz point 
,
Point
is a principal Misiurewicz point of the 1/3 limb. It has 3 external ray
s 9/56, 11/56 and 15/56.
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
(the parameter space
Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
of quadratic polynomials) for which the critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
is strictly preperiodic (i.e., it becomes periodic after finitely many iterations but is not periodic itself). By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set
Multibrot set
In mathematics, a multibrot set is the set of values in the complex plane whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursions z \mapsto z^d + c . \,...
where the unique critical point is strictly preperiodic. (This term makes less sense for maps in greater generality that have more than one (free) critical point because some critical points might be periodic and others not.)
Mathematical notation
A parameter is a Misiurewicz point 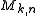if it satisfies the equations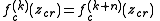and
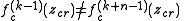
so :
where :
is a critical pointCritical point (mathematics)In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of
,
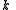and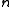 
are positive integers,
and
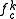denotes the 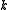-th iterate of 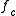.Name
Misiurewicz points are named after the Polish-American mathematicianMathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Michał Misiurewicz
Michał Misiurewicz
Michał Misiurewicz is a Polish mathematician. He is known for his contributions to chaotic dynamical systems and fractal geometry, notably the Misiurewicz point....
.
Note that the term "Misiurewicz point" is used ambiguously: Misiurewicz originally investigated maps in which all critical points were non-recurrent (that is, there is a neighborhood of every critical point that is not visited by the orbit of this critical point), and this meaning is firmly established in the context of dynamics of iterated interval maps. The case that for a quadratic polynomial the unique critical point is strictly preperiodic is only a very special case; in this restricted sense (as described above) this term is used in complex dynamics; a more appropriate term would be Misiurewicz-Thurston points (after William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
who investigated postcritically finite rational maps).
Quadratic maps=
A complex quadratic polynomial
Complex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
has only one critical point. By a suitable conjugation
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
any quadratic polynomial can be transformed into a map of the form
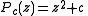which has a single critical point at 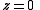. The Misiurewicz points of this family of maps are roots of the equations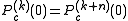,(subject to the condition that the critical point is not periodic),
where :
- k is the pre-period
- n is the period
denotes the n-fold compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of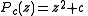
with itself i.e. the nth iterationIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of
.
For example, the Misiurewicz points with k=2 and n=1, denoted by M2,1, are roots of
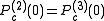
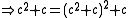
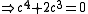.The root c=0 is not a Misiurewicz point because the critical point is a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
when c=0, and so is periodic rather than pre-periodic. This leaves a single Misiurewicz point M2,1 at c = −2.
Properties of Misiurewicz points of complex quadratic mapping
Misiurewicz points belong to the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
. Misiurewicz points are dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
.
If
is a Misiurewicz point, then the associated filled Julia setFilled Julia set
The filled-in Julia set \ K of a polynomial \ f is a Julia set and its interior.-Formal definition:The filled-in Julia set \ K of a polynomial \ f is defined as the set of all points z\, of dynamical plane that have bounded orbit with respect to \ f...
is equal to the Julia set
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
, and means the filled Julia set
Filled Julia set
The filled-in Julia set \ K of a polynomial \ f is a Julia set and its interior.-Formal definition:The filled-in Julia set \ K of a polynomial \ f is defined as the set of all points z\, of dynamical plane that have bounded orbit with respect to \ f...
has no interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
.
If
is a Misiurewicz point, then in the corresponding Julia set all periodic cycles are repelling (in particular the cycle that the critical orbit falls onto).Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
and Julia set
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
are locally asymptotically similarSimilarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
around Misiurewicz points. Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
is self-similar
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
around Misiurewicz points
Types
Misiurewicz points can be classified according to number of external rays that land on them :- branch points ( = points that disconnect the Mandelbrot set into at least three components.) with 3 or more external arguments ( angles )External rayAn external ray is a curve that runs from infinity toward a Julia or Mandelbrot set.This curve is only sometimes a half-line but is called ray because it is image of ray....
- non-branch points with exactly 2 external arguments ( = interior points of arcs within the Mandelbrot set) : these points are less conspicuous and thus not so easily to find on pictures.
- end points with 1 external argument
According to the Branch Theorem of the Mandelbrot set, all branch points of the Mandelbrot set are Misiurewicz points (plus, in a combinatorial sense, hyperbolic components represented by their centers).
Many (actually, most) Misiurewicz parameters in the Mandelbrot set look like `centers of spirals'. The explanation for this is the following: at a Misiurewicz parameter, the critical value jumps onto a repelling periodic cycle after finitely many iterations; at each point on the cycle, the Julia set is asymptotically self-similar by a complex multiplication by the derivative of this cycle. If the derivative is non-real, then this implies that the Julia set, near the periodic cycle, has a spiral structure. A similar spiral structure thus occurs in the Julia set near the critical value and, by Tan Lei's aforementioned theorem, also in the Mandelbrot set near any Misiurewicz parameter for which the repelling orbit has non-real multiplier. Depending on the value of the multiplier, the spiral shape can seem more or less pronounced. The number of the arms at the spiral equals the number of branches at the Misiurewicz parameter, and this equals the number of branches at the critical value in the Julia set. (Even the `principal Misiurewicz point in the 1/3-limb', at the end of the parameter rays at angles 9/56, 11/56, and 15/56, turns out to be asymptotically a spiral, with infinitely many turns, even though this is hard to see without maginification.)
External arguments
External argumentsExternal ray
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set.This curve is only sometimes a half-line but is called ray because it is image of ray....
of Misiurewicz points, measured in turns
Turn (geometry)
A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
are :
- rational numbers
- proper fraction with evenEven and odd numbersIn mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
denominator- dyadic fractions with denominator
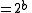and finite ( terminating ) expansion , like :
- dyadic fractions with denominator
-
-
- fraction with denominator
and repeating expansionRepeating decimalIn arithmetic, a decimal representation of a real number is called a repeating decimal if at some point it becomes periodic, that is, if there is some finite sequence of digits that is repeated indefinitely...
like :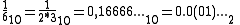
.
- fraction with denominator
-
where :
a and b are positive integers and b is odd ,
subscript number shows base of numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
.
End points
:
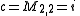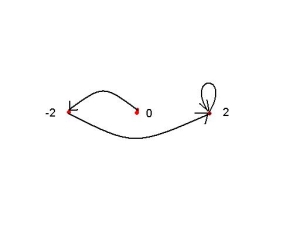
- is a tip of the filament
- Its critical orbits is
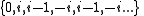
Point
- is the end-point of main antenna of Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
- Its critical orbits is
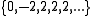
- Symbolic sequenceSymbolic dynamicsIn mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
= C L R R R ... - preperiod is 2 and period 1
Notice that it is z-plane (dynamical plane
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
) not c-plane (parameter plane
Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
) and point
is not the same point as 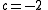.Point
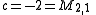is landing point of only one external rayExternal ray
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set.This curve is only sometimes a half-line but is called ray because it is image of ray....
( parameter ray) of angle 1/2 .
Non-Branch points
Point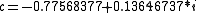 is near a Misiurewicz point 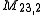. It is
- a center of a two-arms spiral
- a landing point of 2 external rays with angles :
and 
where denominator is 
- preperiodic point with preperiod
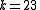and period 
Point
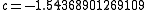is near a Misiurewicz point ,
- which is landing point for pair of rays :
,
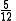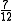
- has preperiod
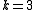and period 
Branch points
Point
is a principal Misiurewicz point of the 1/3 limb. It has 3 external rayExternal ray
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set.This curve is only sometimes a half-line but is called ray because it is image of ray....
s 9/56, 11/56 and 15/56.
External links
- Preperiodic (Misiurewicz) points in the Mandelbrot set by Evgeny Demidov
- M & J-sets similarity for preperiodic points. Lei's theorem by Douglas C. Ravenel
- Misiurewicz Point of the logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
by J. C. Sprott