Electromagnetic mass
Encyclopedia
Electromagnetic mass was initially a concept of classical mechanics
, denoting as to how much the electromagnetic field
, or the self-energy
, is contributing to the mass of charged particles. It was first derived by J. J. Thomson
in 1881 and was for some time also considered as a dynamical explanation of inertial mass per se. Today, the relation of mass to energy, including electromagnetic energy, is interpreted kinematically
on the basis of Albert Einstein
's Mass–energy equivalence. As to the cause of mass itself, the Higgs mechanism
in the framework of the relativistic Standard Model
is currently used. In addition, some problems concerning the electromagnetic mass and self-energy of charged particles are still studied.
in 1881 that a charged sphere moving in a space filled with a medium of a specific inductive capacity (the electromagnetic aether
of James Clerk Maxwell
), is harder to set in motion than an uncharged body. (Similar considerations were already made by George Gabriel Stokes
(1843) with respect to hydrodynamics, who showed that the inertia of a body moving in an incompressible perfect fluid
is increased.) So due to this self-induction effect, electrostatic energy behaves as having some sort of momentum
and "apparent" electromagnetic mass, which can increase the ordinary mechanical mass of the bodies, or in more modern terms, the increase should arise from their electromagnetic self-energy
. This idea was worked out in more detail by Oliver Heaviside
(1889), Thomson (1893), George Frederick Charles Searle
(1897), Max Abraham
(1902), Hendrik Lorentz
(1892, 1904), and was directly applied to the electron
by using the Abraham–Lorentz force. Now, the electrostatic energy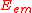
and mass 
of an electron at rest was calculated to be Feynman, Ch. 28Pais, pp. 155-159Miller, pp. 45-47, 102-103
where
the uniformly distributed charge, 
is the classical electron radius
which has to be finite to avoid infinite energy accumulation. Thus the formula for this electromagnetic energy-mass-relation is
This was discussed in connection with the proposal of the electrical origin of matter, so Wilhelm Wien
(1900), and Abraham (1902), came to the conclusion that the total mass of the bodies is identical to its electromagnetic mass. Wien stated, that if it is assumed that gravitation
is an electromagnetic effect too, then there has to be a proportionality between electromagnetic energy, inertial mass, and gravitational mass. When one body attracts another one, the electromagnetic energy store of gravitation is according to Wien diminished by the amount (where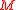
is the attracted mass, 
the gravitational constant
,
the distance):
Henri Poincaré
in 1906 argued that when mass is in fact the product of the electromagnetic field in the aether – implying that no "real" mass exists – and because matter is inseparably connected with mass, then also matter
doesn't exist at all and electrons are only concavities in the aether.
In 1897, Searle gave a more precise formula for the electromagnetic energy of charged sphere in motion:
and like Thomson he concluded:
(1901) and Abraham (1902) derived the formula for the electromagnetic mass of moving bodies:
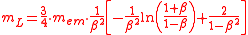
However, it was shown by Abraham (1902), that this value is only valid in the longitudinal direction ("longitudinal mass"), i.e., that the electromagnetic mass also depends on the direction of the moving bodies with respect to the aether. Thus Abraham also derived the "transverse mass":
On the other hand, already in 1899 Lorentz assumed that the electrons undergo length contraction
in the line of motion, which leads to results for the acceleration of moving electrons that differ from those given by Abraham. Lorentz obtained factors of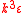
parallel to the direction of motion and 
perpendicular to the direction of motion, where 
and 
is an undetermined factor. Lorentz expanded his 1899 ideas in his famous 1904 paper, where he set the factor 
to unity, thus:
,
So, eventually Lorentz arrived at the same conclusion as Thomson in 1893: no body can reach the speed of light because the mass becomes infinitely large at this velocity.
Additionally, a third electron model was developed by Alfred Bucherer
and Paul Langevin
, in which the electron contracts in the line of motion, and expands perpendicular to it, so that the volume remains constant. This gives:
(1901), but the experiments were not precise enough, to distinguish between them. In 1905 Kaufmann conducted another series of experiments (Kaufmann–Bucherer–Neumann experiments
), which confirmed Abraham's and Bucherer's predictions, but contradicted Lorentz's theory and the "fundamental assumption of Lorentz and Einstein", i.e., the relativity principle. However, in the following years experiments by Alfred Bucherer
(1908), Neumann (1914) and others seemed to confirm Lorentz's mass formula. However, it was later pointed out, that the Bucherer-Neumann experiments were also not precise enough to distinguish between the theories - it lasted until 1940 when the precision required was achieved to eventually prove Lorentz's formula and to refute Abraham's by this kind of experiments (other experiments of different kind already refuted Abraham's and Bucherer's formulas long before).Miller (1981), 334-352
, depending on whether the mass is calculated from its energy or its momentum, so a non-electromagnetic potential (corresponding to 1/3 of the Electron's electromagnetic energy) was necessary to render these masses equal. Abraham doubted whether it was possible to develop a model satisfying all of these properties.
To solve those problems, Henri Poincaré
in 1905 and 1906 introduced some sort of pressure ("Poincaré stresses") of non-electromagnetic nature. As required by Abraham, these stresses contribute non-electromagnetic energy to the electrons, amounting to 1/4 of their total energy or to 1/3 of their electromagnetic energy. So, the Poincaré stresses remove the contradiction in the derivation of the longitudinal electromagnetic mass, they prevent the electron from exploding, they remain unaltered by a Lorentz transformation
(i.e. they are Lorentz invariant), and were also thought as a dynamical explanation of length contraction
. However, Poincaré still assumed that only the electromagnetic energy contributes to the mass of the bodies.Janssen/Mecklenburg (2007)
As it was later noted, the problem lies in the 4/3 factor of electromagnetic rest mass - given above as
when derived from the Abraham-Lorentz equations. However, when it is derived from the electron's electrostatic energy alone, we have 
where the 4/3 factor is missing. This can be solved by adding the non-electromagnetic energy 
of the Poincaré stresses to 
, the electron's total energy 
now becomes:
Thus the missing 4/3 factor is restored when the mass is related to its electromagnetic energy, and it disappears when the total energy is considered.Miller (1981), 382-383Janssen/Mecklenburg (2007), pp. 32, 40
. These pressures or tensions in the electromagnetic field were derived by James Clerk Maxwell
(1874) and Adolfo Bartoli
(1876). Lorentz recognized in 1895 that those tensions also arise in his theory
of the stationary aether. So if the electromagnetic field of the aether is able to set bodies in motion, the action/reaction principle demands that the aether must be set in motion by matter as well. However, Lorentz pointed out that any tension in the aether requires the mobility of the aether parts, which in not possible since in his theory the aether is immobile. This represents a violation of the reaction principle that was accepted by Lorentz consciously. He continued by saying, that one can only speak about fictitious tensions, since they are only mathematical models in his theory to ease the description of the electrodynamic interactions.
still moves with a uniform velocity when electromagnetic fields and radiation are involved. He noticed that the action/reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum (such a momentum was also derived by Thomson in 1893 in a more complicated way). Poincaré concluded, the electromagnetic field energy behaves like a fictitious fluid
(„fluide fictif“) with a mass density of
(in other words 
). Now, if the center of mass frame (COM-frame) is defined by both the mass of matter and the mass of the fictitious fluid, and if the fictitious fluid is indestructible - it's neither created or destroyed - then the motion of the center of mass frame remains uniform.
But this electromagnetic fluid is not indestructible, because it can be absorbed by matter (which according to Poincaré was the reason why he regarded the em-fluid as "fictitious" rather than "real"). Thus the COM-principle would be violated again. As it was later done by Einstein, an easy solution of this would be to assume that the mass of em-field is transferred to matter in the absorption process. But Poincaré created another solution: He assumed that there exists an immobile non-electromagnetic energy fluid at each point in space, also carrying a mass proportional to its energy. When the fictitious em-fluid is destroyed or absorbed, its electromagnetic energy and mass is not carried away by moving matter, but is transferred into the non-electromagnetic fluid and remains at exactly the same place in that fluid. (Poincaré added that one should not be too surprised by these assumptions, since they are only mathematical fictions.) In this way, the motion of the COM-frame, incl. matter, fictitious em-fluid, and fictitious non-em-fluid, at least theoretically remains uniform.
However, since only matter and electromagnetic energy are directly observable by experiment (not the non-em-fluid), Poincaré's resolution still violates the reaction principle and the COM-theorem, when an emission/absorption process is practically considered. This leads to a paradox when changing frames: if waves are radiated in a certain direction, the device will suffer a recoil
from the momentum of the fictitious fluid. Then, Poincaré performed a Lorentz boost
(to first order in v/c) to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow perpetual motion
, a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold. Therefore he argued that also in this case there has to be another compensating mechanism in the ether.Miller (1981), 41ffDarrigol (2005), 18-21
Poincaré came back to this topic in 1904. This time he rejected his own solution that motions in the ether can compensate the motion of matter, because any such motion is unobservable and therefore scientifically worthless. He also abandoned the concept that energy carries mass and wrote in connection to the above mentioned recoil:
per cm3 and 
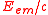per cm2. Contrary to Lorentz and Poincaré, who considered momentum as a fictitious force, he argued that it is a real physical entity, and therefore conservation of momentum is guaranteed.
By studying the dynamics of a moving cavity
, Friedrich Hasenöhrl
(1904) concluded that radiation and thus temperature contribute to the inertia of bodies. He derived the formula
, where 
is the "apparent mass" due to radiation. This was corrected in 1905 by Abraham and him to 
(the same formula as for the electromagnetic rest mass).Miller (1981), 359-360
found out in 1905, that kinematic considerations based on special relativity require that all forms of energy (not only electromagnetic) contribute to the mass of bodies (Mass–energy equivalence). That is, the entire mass of a body is a measure of its energy content by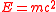
, and Einstein's considerations were independent from assumptions about the constitution of matter. By this equivalence, Poincaré's radiation paradox can be solved without using "compensating forces", because the mass of matter itself (not the non-electromagnetic aether fluid as suggested by Poincaré) is increased or diminished by the mass of electromagnetic energy in the course of the emission/absorption process. Also the idea of an electromagnetic explanation of gravitation was superseded in the course of developing general relativity
.
So every theory dealing with the mass of a body, must be formulated in a relativistic way from the outset. This is for example the case in the current quantum field
explanation of mass in the framework of the Standard Model
, the Higgs mechanism
. Because of this, the idea that any form of mass is completely caused by interactions with electromagnetic fields, is not relevant any more.
However, the introduction of an "effective" electromagnetic mass is still useful, when it is about the special case of the electromagnetic self-energy of charged particles, and many different reformulations of the Abraham-Lorentz equations have been derived (to deal with the 4/3-problem for example, see next section). Such questions are also discussed in connection with Renormalization
, and on the basis of quantum mechanics
and quantum field theory
, which must be applied when the electron is considered physically point-like. For distances located in the classical domain, the classical concepts again come into play.Rohrlich (1997)
in 1911 also used the Abraham-Lorentz equations of motion in his development of special relativistic dynamics, so that also in special relativity the 4/3-factor is present when the electromagnetic mass of a charged sphere is calculated. This contradicts the mass-energy equivalence formula, which requires the relation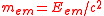
without the 4/3 factor, or in other words, four-momentum doesn't properly transform like a four-vector
when the 4/3 factor is present. Laue found a solution equivalent to Poincaré's introduction of a non-electromagnetic potential (Poincaré stresses), but Laue showed its deeper, kinematic meaning by employing and advancing Hermann Minkowski
's space-time formalism. Laue's formalism required that there are additional components and forces, which guarantee that spatially extended systems (where both electromagnetic and non-electromagnetic energies are combined) are forming a stable or "closed system" and transform as a four-vector. That is, only with respect to electromagnetic mass the 4/3 factor exists, while the complete and closed system has total rest-mass and energy of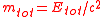
.
A more elegant solution was found by Enrico Fermi
(1922), Paul Dirac
(1938) and Fritz Rohrlich (1960), who pointed out that the electron's stability and the 4/3-problem are two different things. They showed that the preceding definitions of four-momentum are non-relativistic per se, and by changing the definition into a relativistic form, the electromagnetic mass can simply written as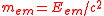
and thus the 4/3 factor doesn't appear at all. So every part of the system, not only "closed" systems, properly transforms as a four-vector. However, binding forces like the Poincaré stresses are still necessary to prevent the electron from exploding due to Coulomb repulsion. But on the basis of the Fermi-Rohrlich definition, this is only a dynamical problem and has nothing to do with the transformation properties any more.
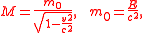
by physicists like Richard Chace Tolman and is sometimes used in physics textbooks up to this day, although the term 'mass' is now considered by many to refer to invariant mass
.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, denoting as to how much the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
, or the self-energy
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
, is contributing to the mass of charged particles. It was first derived by J. J. Thomson
J. J. Thomson
Sir Joseph John "J. J." Thomson, OM, FRS was a British physicist and Nobel laureate. He is credited for the discovery of the electron and of isotopes, and the invention of the mass spectrometer...
in 1881 and was for some time also considered as a dynamical explanation of inertial mass per se. Today, the relation of mass to energy, including electromagnetic energy, is interpreted kinematically
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
on the basis of Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's Mass–energy equivalence. As to the cause of mass itself, the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
in the framework of the relativistic Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
is currently used. In addition, some problems concerning the electromagnetic mass and self-energy of charged particles are still studied.
Rest mass and energy
It was recognized by J. J. ThomsonJ. J. Thomson
Sir Joseph John "J. J." Thomson, OM, FRS was a British physicist and Nobel laureate. He is credited for the discovery of the electron and of isotopes, and the invention of the mass spectrometer...
in 1881 that a charged sphere moving in a space filled with a medium of a specific inductive capacity (the electromagnetic aether
Luminiferous aether
In the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....
of James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
), is harder to set in motion than an uncharged body. (Similar considerations were already made by George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
(1843) with respect to hydrodynamics, who showed that the inertia of a body moving in an incompressible perfect fluid
Perfect fluid
In physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
is increased.) So due to this self-induction effect, electrostatic energy behaves as having some sort of momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
and "apparent" electromagnetic mass, which can increase the ordinary mechanical mass of the bodies, or in more modern terms, the increase should arise from their electromagnetic self-energy
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
. This idea was worked out in more detail by Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
(1889), Thomson (1893), George Frederick Charles Searle
George Frederick Charles Searle
George Frederick Charles Searle was a British physicist and teacher, and a Fellow of the Royal Society.-Biography:Searle was born in Oakington, Cambridgeshire, England....
(1897), Max Abraham
Max Abraham
Max Abraham was a German physicist.Abraham was born in Danzig, Imperial Germany to a family of Jewish merchants. His father was Moritz Abraham and his mother was Selma Moritzsohn. Attending the University of Berlin, he studied under Max Planck. He graduated in 1897...
(1902), Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
(1892, 1904), and was directly applied to the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
by using the Abraham–Lorentz force. Now, the electrostatic energy
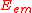and mass of an electron at rest was calculated to be Feynman, Ch. 28Pais, pp. 155-159Miller, pp. 45-47, 102-103where
the uniformly distributed charge, is the classical electron radiusClassical electron radius
The classical electron radius, also known as the Lorentz radius or the Thomson scattering length, is based on a classical relativistic model of the electron...
which has to be finite to avoid infinite energy accumulation. Thus the formula for this electromagnetic energy-mass-relation is
This was discussed in connection with the proposal of the electrical origin of matter, so Wilhelm Wien
Wilhelm Wien
Wilhelm Carl Werner Otto Fritz Franz Wien was a German physicist who, in 1893, used theories about heat and electromagnetism to deduce Wien's displacement law, which calculates the emission of a blackbody at any temperature from the emission at any one reference temperature.He also formulated an...
(1900), and Abraham (1902), came to the conclusion that the total mass of the bodies is identical to its electromagnetic mass. Wien stated, that if it is assumed that gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
is an electromagnetic effect too, then there has to be a proportionality between electromagnetic energy, inertial mass, and gravitational mass. When one body attracts another one, the electromagnetic energy store of gravitation is according to Wien diminished by the amount (where
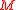is the attracted mass, the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
,
the distance):Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
in 1906 argued that when mass is in fact the product of the electromagnetic field in the aether – implying that no "real" mass exists – and because matter is inseparably connected with mass, then also matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
doesn't exist at all and electrons are only concavities in the aether.
Thomson and Searle
Thomson (1893) noticed that electromagnetic momentum and energy of charged bodies and therefore their masses depend on the speed of the bodies as well. He wrote:In 1897, Searle gave a more precise formula for the electromagnetic energy of charged sphere in motion:
and like Thomson he concluded:
Longitudinal and transverse mass
From Searle's formula, Walter KaufmannWalter Kaufmann (physicist)
Walter Kaufmann was a German physicist. He is most well known for his first experimental proof of the velocity dependence of mass, which was an important contribution to the development of modern physics, including special relativity.-Life:In 1890/91 he studied mechanical engineering at the...
(1901) and Abraham (1902) derived the formula for the electromagnetic mass of moving bodies:
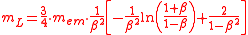
However, it was shown by Abraham (1902), that this value is only valid in the longitudinal direction ("longitudinal mass"), i.e., that the electromagnetic mass also depends on the direction of the moving bodies with respect to the aether. Thus Abraham also derived the "transverse mass":
On the other hand, already in 1899 Lorentz assumed that the electrons undergo length contraction
Length contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
in the line of motion, which leads to results for the acceleration of moving electrons that differ from those given by Abraham. Lorentz obtained factors of
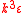parallel to the direction of motion and perpendicular to the direction of motion, where and is an undetermined factor. Lorentz expanded his 1899 ideas in his famous 1904 paper, where he set the factor to unity, thus:,So, eventually Lorentz arrived at the same conclusion as Thomson in 1893: no body can reach the speed of light because the mass becomes infinitely large at this velocity.
Additionally, a third electron model was developed by Alfred Bucherer
Alfred Bucherer
Alfred Heinrich Bucherer was a German physicist, who is known for his experiments on relativistic mass...
and Paul Langevin
Paul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
, in which the electron contracts in the line of motion, and expands perpendicular to it, so that the volume remains constant. This gives:
Kaufmann's experiments
The predictions of the theories of Abraham an Lorentz were supported by the experiments of Walter KaufmannWalter Kaufmann (physicist)
Walter Kaufmann was a German physicist. He is most well known for his first experimental proof of the velocity dependence of mass, which was an important contribution to the development of modern physics, including special relativity.-Life:In 1890/91 he studied mechanical engineering at the...
(1901), but the experiments were not precise enough, to distinguish between them. In 1905 Kaufmann conducted another series of experiments (Kaufmann–Bucherer–Neumann experiments
Kaufmann–Bucherer–Neumann experiments
The Kaufmann-Bucherer-Neumann experiments measured the dependence of the inertial mass of an object on its velocity. The historical importance of a series of this experiment performed by various physicists between 1901 and 1915 is due to the results being used to test the predictions of special...
), which confirmed Abraham's and Bucherer's predictions, but contradicted Lorentz's theory and the "fundamental assumption of Lorentz and Einstein", i.e., the relativity principle. However, in the following years experiments by Alfred Bucherer
Alfred Bucherer
Alfred Heinrich Bucherer was a German physicist, who is known for his experiments on relativistic mass...
(1908), Neumann (1914) and others seemed to confirm Lorentz's mass formula. However, it was later pointed out, that the Bucherer-Neumann experiments were also not precise enough to distinguish between the theories - it lasted until 1940 when the precision required was achieved to eventually prove Lorentz's formula and to refute Abraham's by this kind of experiments (other experiments of different kind already refuted Abraham's and Bucherer's formulas long before).Miller (1981), 334-352
Poincaré stresses and 4/3 problem
The idea of an electromagnetic nature of matter, however, had to be given up. Abraham (1904, 1905) argued that non-electromagnetic forces were necessary to prevent Lorentz's contractile electrons from exploding. He also showed that different results for the longitudinal electromagnetic mass can be obtained in Lorentz's theoryLorentz ether theory
What is now often called Lorentz Ether theory has its roots in Hendrik Lorentz's "Theory of electrons", which was the final point in the development of the classical aether theories at the end of the 19th and at the beginning of the 20th century....
, depending on whether the mass is calculated from its energy or its momentum, so a non-electromagnetic potential (corresponding to 1/3 of the Electron's electromagnetic energy) was necessary to render these masses equal. Abraham doubted whether it was possible to develop a model satisfying all of these properties.
To solve those problems, Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
in 1905 and 1906 introduced some sort of pressure ("Poincaré stresses") of non-electromagnetic nature. As required by Abraham, these stresses contribute non-electromagnetic energy to the electrons, amounting to 1/4 of their total energy or to 1/3 of their electromagnetic energy. So, the Poincaré stresses remove the contradiction in the derivation of the longitudinal electromagnetic mass, they prevent the electron from exploding, they remain unaltered by a Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
(i.e. they are Lorentz invariant), and were also thought as a dynamical explanation of length contraction
Length contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
. However, Poincaré still assumed that only the electromagnetic energy contributes to the mass of the bodies.Janssen/Mecklenburg (2007)
As it was later noted, the problem lies in the 4/3 factor of electromagnetic rest mass - given above as
when derived from the Abraham-Lorentz equations. However, when it is derived from the electron's electrostatic energy alone, we have where the 4/3 factor is missing. This can be solved by adding the non-electromagnetic energy of the Poincaré stresses to , the electron's total energy now becomes:Thus the missing 4/3 factor is restored when the mass is related to its electromagnetic energy, and it disappears when the total energy is considered.Miller (1981), 382-383Janssen/Mecklenburg (2007), pp. 32, 40
Radiation pressure
Another way of deriving some sort of electromagnetic mass was based on the concept of radiation pressureRadiation pressure
Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
. These pressures or tensions in the electromagnetic field were derived by James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
(1874) and Adolfo Bartoli
Adolfo Bartoli
Adolfo Bartoli was an Italian physicist, who is best known for introducing the concept of radiation pressure from thermodynamical considerations....
(1876). Lorentz recognized in 1895 that those tensions also arise in his theory
Lorentz ether theory
What is now often called Lorentz Ether theory has its roots in Hendrik Lorentz's "Theory of electrons", which was the final point in the development of the classical aether theories at the end of the 19th and at the beginning of the 20th century....
of the stationary aether. So if the electromagnetic field of the aether is able to set bodies in motion, the action/reaction principle demands that the aether must be set in motion by matter as well. However, Lorentz pointed out that any tension in the aether requires the mobility of the aether parts, which in not possible since in his theory the aether is immobile. This represents a violation of the reaction principle that was accepted by Lorentz consciously. He continued by saying, that one can only speak about fictitious tensions, since they are only mathematical models in his theory to ease the description of the electrodynamic interactions.
Mass of the fictitious electromagnetic fluid
In 1900 Poincaré studied the conflict between the action/reaction principle and Lorentz's theory. He tried to determine whether the center of gravityCenter of gravity
In physics, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass serves as the center of gravity...
still moves with a uniform velocity when electromagnetic fields and radiation are involved. He noticed that the action/reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum (such a momentum was also derived by Thomson in 1893 in a more complicated way). Poincaré concluded, the electromagnetic field energy behaves like a fictitious fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
(„fluide fictif“) with a mass density of
(in other words ). Now, if the center of mass frame (COM-frame) is defined by both the mass of matter and the mass of the fictitious fluid, and if the fictitious fluid is indestructible - it's neither created or destroyed - then the motion of the center of mass frame remains uniform.But this electromagnetic fluid is not indestructible, because it can be absorbed by matter (which according to Poincaré was the reason why he regarded the em-fluid as "fictitious" rather than "real"). Thus the COM-principle would be violated again. As it was later done by Einstein, an easy solution of this would be to assume that the mass of em-field is transferred to matter in the absorption process. But Poincaré created another solution: He assumed that there exists an immobile non-electromagnetic energy fluid at each point in space, also carrying a mass proportional to its energy. When the fictitious em-fluid is destroyed or absorbed, its electromagnetic energy and mass is not carried away by moving matter, but is transferred into the non-electromagnetic fluid and remains at exactly the same place in that fluid. (Poincaré added that one should not be too surprised by these assumptions, since they are only mathematical fictions.) In this way, the motion of the COM-frame, incl. matter, fictitious em-fluid, and fictitious non-em-fluid, at least theoretically remains uniform.
However, since only matter and electromagnetic energy are directly observable by experiment (not the non-em-fluid), Poincaré's resolution still violates the reaction principle and the COM-theorem, when an emission/absorption process is practically considered. This leads to a paradox when changing frames: if waves are radiated in a certain direction, the device will suffer a recoil
Recoil
Recoil is the backward momentum of a gun when it is discharged. In technical terms, the recoil caused by the gun exactly balances the forward momentum of the projectile and exhaust gasses, according to Newton's third law...
from the momentum of the fictitious fluid. Then, Poincaré performed a Lorentz boost
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
(to first order in v/c) to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow perpetual motion
Perpetual motion
Perpetual motion describes hypothetical machines that operate or produce useful work indefinitely and, more generally, hypothetical machines that produce more work or energy than they consume, whether they might operate indefinitely or not....
, a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold. Therefore he argued that also in this case there has to be another compensating mechanism in the ether.Miller (1981), 41ffDarrigol (2005), 18-21
Poincaré came back to this topic in 1904. This time he rejected his own solution that motions in the ether can compensate the motion of matter, because any such motion is unobservable and therefore scientifically worthless. He also abandoned the concept that energy carries mass and wrote in connection to the above mentioned recoil:
Momentum and cavity radiation
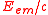However, Poincaré's idea of momentum and mass associated with radiation proved to be fruitful, when Abraham introduced the term „electromagnetic momentum“, having a field density of per cm3 and per cm2. Contrary to Lorentz and Poincaré, who considered momentum as a fictitious force, he argued that it is a real physical entity, and therefore conservation of momentum is guaranteed.By studying the dynamics of a moving cavity
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
, Friedrich Hasenöhrl
Friedrich Hasenöhrl
Friedrich Hasenöhrl , was an Austro-Hungarian physicist.-Life:Friedrich Hasenöhrl was born in Vienna, Austria in 1874. His father was a lawyer and his mother belonged to a prominent aristocratic family...
(1904) concluded that radiation and thus temperature contribute to the inertia of bodies. He derived the formula
, where is the "apparent mass" due to radiation. This was corrected in 1905 by Abraham and him to (the same formula as for the electromagnetic rest mass).Miller (1981), 359-360Mass–energy equivalence
The idea that the principal relation of mass and energy can be solely explained by considering the dynamical interactions of matter was superseded, when Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
found out in 1905, that kinematic considerations based on special relativity require that all forms of energy (not only electromagnetic) contribute to the mass of bodies (Mass–energy equivalence). That is, the entire mass of a body is a measure of its energy content by
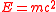, and Einstein's considerations were independent from assumptions about the constitution of matter. By this equivalence, Poincaré's radiation paradox can be solved without using "compensating forces", because the mass of matter itself (not the non-electromagnetic aether fluid as suggested by Poincaré) is increased or diminished by the mass of electromagnetic energy in the course of the emission/absorption process. Also the idea of an electromagnetic explanation of gravitation was superseded in the course of developing general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
So every theory dealing with the mass of a body, must be formulated in a relativistic way from the outset. This is for example the case in the current quantum field
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
explanation of mass in the framework of the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
. Because of this, the idea that any form of mass is completely caused by interactions with electromagnetic fields, is not relevant any more.
However, the introduction of an "effective" electromagnetic mass is still useful, when it is about the special case of the electromagnetic self-energy of charged particles, and many different reformulations of the Abraham-Lorentz equations have been derived (to deal with the 4/3-problem for example, see next section). Such questions are also discussed in connection with Renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, and on the basis of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, which must be applied when the electron is considered physically point-like. For distances located in the classical domain, the classical concepts again come into play.Rohrlich (1997)
4/3 problem
Max von LaueMax von Laue
Max Theodor Felix von Laue was a German physicist who won the Nobel Prize in Physics in 1914 for his discovery of the diffraction of X-rays by crystals...
in 1911 also used the Abraham-Lorentz equations of motion in his development of special relativistic dynamics, so that also in special relativity the 4/3-factor is present when the electromagnetic mass of a charged sphere is calculated. This contradicts the mass-energy equivalence formula, which requires the relation
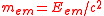without the 4/3 factor, or in other words, four-momentum doesn't properly transform like a four-vectorFour-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
when the 4/3 factor is present. Laue found a solution equivalent to Poincaré's introduction of a non-electromagnetic potential (Poincaré stresses), but Laue showed its deeper, kinematic meaning by employing and advancing Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
's space-time formalism. Laue's formalism required that there are additional components and forces, which guarantee that spatially extended systems (where both electromagnetic and non-electromagnetic energies are combined) are forming a stable or "closed system" and transform as a four-vector. That is, only with respect to electromagnetic mass the 4/3 factor exists, while the complete and closed system has total rest-mass and energy of
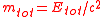.A more elegant solution was found by Enrico Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
(1922), Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
(1938) and Fritz Rohrlich (1960), who pointed out that the electron's stability and the 4/3-problem are two different things. They showed that the preceding definitions of four-momentum are non-relativistic per se, and by changing the definition into a relativistic form, the electromagnetic mass can simply written as
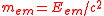and thus the 4/3 factor doesn't appear at all. So every part of the system, not only "closed" systems, properly transforms as a four-vector. However, binding forces like the Poincaré stresses are still necessary to prevent the electron from exploding due to Coulomb repulsion. But on the basis of the Fermi-Rohrlich definition, this is only a dynamical problem and has nothing to do with the transformation properties any more.Relativistic mass
The concepts of longitudinal and transverse mass (equivalent to those of Lorentz) were also used by Einstein in his first papers on relativity. However, in special relativity they apply to the entire mass of matter, not only to the electromagnetic part. Later a similar concept was also used as relativistic massMass in special relativity
Mass in special relativity incorporates the general understandings from the concept of mass-energy equivalence. Added to this concept is an additional complication resulting from the fact that "mass" is defined in two different ways in special relativity: one way defines mass as an invariant...
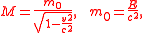
by physicists like Richard Chace Tolman and is sometimes used in physics textbooks up to this day, although the term 'mass' is now considered by many to refer to invariant mass
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
.
See also
- History of special relativityHistory of special relativityThe history of special relativity consists of many theoretical results and empirical findings obtained by Albert Michelson, Hendrik Lorentz, Henri Poincaré and others...
- Abraham–Lorentz force
- Abraham–Lorentz–Dirac force
- Wheeler-Feynman absorber theory