Convex regular 4-polytope
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a convex regular 4-polytope is a 4-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
that is both regular
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
and convex
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
. These are the four-dimensional analogs of the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s (in three dimensions) and the regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s (in two dimensions).
These polytopes were first described by the Swiss mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Ludwig Schläfli
Ludwig Schläfli
Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
in the mid-19th century. Schläfli discovered that there are precisely six such figures. Five of these may be thought of as higher dimensional analogs of the Platonic solids. There is one additional figure (the 24-cell) which has no three-dimensional equivalent.
Each convex regular 4-polytope is bounded by a set of 3-dimensional cells which are all Platonic solids of the same type and size. These are fitted together along their respective faces in a regular fashion.
Properties
The following tables lists some properties of the six convex regular 4-dimensional polytopes. The symmetry groups of these polytopes are all Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s and given in the notation described in that article. The number following the name of the group is the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of the group.
| Names | Family | Schläfli symbol |
Vertices | Edges | Faces | Cells | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... s |
Dual polytope | Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
|
|---|---|---|---|---|---|---|---|---|---|---|
| 5-cell pentatope hyperpyramid hypertetrahedron 4-simplex |
simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... (n-simplex) |
{3,3,3} | 5 | 10 | 10 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s |
5 tetrahedra |
tetrahedra | (self-dual) | A4 | 120 |
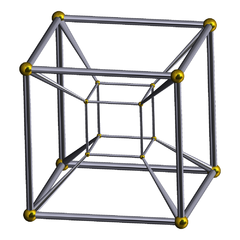
| 8-cell Tesseract hypercube 4-cube |
hypercube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... (n-cube) |
{4,3,3} | 16 | 32 | 24 square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s |
8 cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... s |
tetrahedra | 16-cell | B4 | 384 |
| 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... orthoplex hyperoctahedron 4-orthoplex |
cross-polytope Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... (n-orthoplex) |
{3,3,4} | 8 | 24 | 32 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s |
16 tetrahedra |
octahedra | tesseract | B4 | 384 |
| 24-cell octaplex polyoctahedron |
{3,4,3} | 24 | 96 | 96 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s |
24 octahedra |
cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... s |
(self-dual) | F4 | 1152 | |
| 120-cell dodecaplex hyperdodecahedron polydodecahedron |
{5,3,3} | 600 | 1200 | 720 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s |
120 dodecahedra |
tetrahedra | 600-cell | H4 | 14400 | |
| 600-cell tetraplex hypericosahedron polytetrahedron |
{3,3,5} | 120 | 720 | 1200 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s |
600 tetrahedra |
icosahedra | 120-cell | H4 | 14400 |
Since the boundaries of each of these figures is topologically equivalent
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to a 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
, whose Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
is zero, we have the 4-dimensional analog of Euler's polyhedral formula:

where Nk denotes the number of k-faces in the polytope (a vertex is a 0-face, an edge is a 1-face, etc.).
Visualizations
The following table shows some 2 dimensional projections of these polytopes. Various other visualizations can be found in the external links below. The Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
graphs are also given below the Schläfli symbol.
| 5-cell | 8-cell | 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
24-cell | 120-cell | 600-cell |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
| Wireframe orthographic projection Orthographic projection Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface... s inside Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... s. |
|||||
| Solid orthographic projection Orthographic projection Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface... s |
|||||
 tetrahedral envelope Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... (cell/vertex-centered) |
 cubic envelope Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (cell-centered) |
Cubic envelope Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (cell-centered) |
 cuboctahedral envelope Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... (cell-centered) |
 truncated rhombic triacontahedron envelope Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.... (cell-centered) |
 Pentakis icosidodecahedral envelope Pentakis icosidodecahedron The pentakis icosidodecahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It a dual of the truncated rhombic triacontahedron.... (vertex-centered) |
| Wireframe Schlegel diagrams (Perspective projection) | |||||
 (Cell-centered) |
 (Cell-centered) |
 (Cell-centered) |
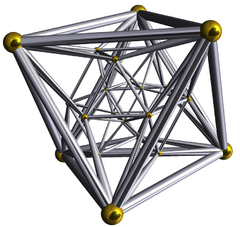 (Cell-centered) |
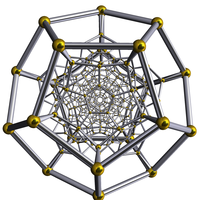 (Cell-centered) |
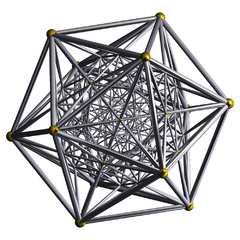 (Vertex-centered) |
| Wireframe stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... s (Hyperspherical) |
|||||
 |
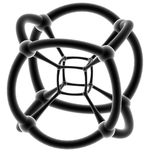 |
 |
 |
 |
 |
See also
- Infinite regular 4-polytopes:
- One regular Euclidean honeycomb: {4,3,4}
- Four regular hyperbolic honeycombs: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
- Nonconvex regular 4-polytopes:
- Schläfli-Hess polychoron - Ten nonconvex regular 4-polytopes
- Abstract regular polychoraAbstract polytopeIn mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
: - Uniform polychoronUniform polychoronIn geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
4-polytope families constructed from the from these 6 regular forms. - Regular polytopeRegular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
- Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
External links
- Jonathan Bowers, 16 regular polychora
- Regular 4D Polytope Foldouts
- Catalog of Polytope Images A collection of stereographic projections of 4-polytopes.
- A Catalog of Uniform Polytopes
- Dimensions 2 hour film about the fourth dimension (contains stereographic projections of all regular polychorons)

