Schlegel diagram Centered on cuboctahedron tetrahedral cells shown
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t1{4,3,3} t0,2{31,1,1}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s
Cells	24	8 (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... 16 (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
Faces	88	64 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 24 {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
Edges	96
Vertices	32
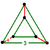Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	(Elongated equilateral-triangular prism)
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	B4 [3,3,4] D4 [31,1,1]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , edge-transitive
Uniform index	10 Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... 11 12 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the rectified tesseract, or rectified 8-cell is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

 (4-dimensional polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

) bounded by 24 cells: 8 cuboctahedra

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

, and 16 tetrahedra

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

.

It has two uniform constructions, as a rectified 8-cell t₁{4,3,3} and a cantellated demitesseract, t_0,2{3^1,1,1}, the second alternating with two types of tetrahedral cells.

Construction

The rectified tesseract may be constructed from the tesseract

Tesseract

In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

 by truncating

Rectification (geometry)

In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...

 its vertices at the midpoints of its edges.

The Cartesian coordinates of the vertices of the rectified tesseract with edge length 2 is given by all permutations of:

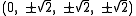
Images

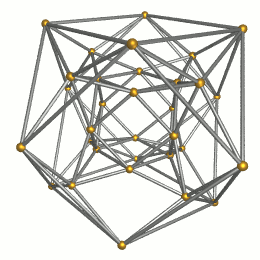Wireframe

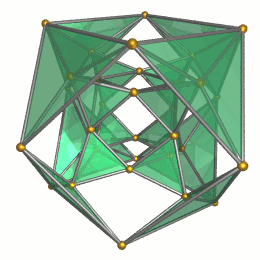16 tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...  cells

Projections

In the cuboctahedron-first parallel projection of the rectified tesseract into 3-dimensional space, the image has the following layout:

• The projection envelope is a cube
  Cube
  In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
  
  .
• A cuboctahedron is inscribed in this cube, with its vertices lying at the midpoint of the cube's edges. The cuboctahedron is the image of two of the cuboctahedral cells.
• The remaining 6 cuboctahedral cells are projected to the square faces of the cube.
• The 8 tetrahedral volumes lying at the triangular faces of the central cuboctahedron are the images of the 16 tetrahedral cells, two cells to each image.

Alternative names

• Rit (Jonathan Bowers: for rectified tesseract)
• Ambotesseract (Neil Sloane & John Horton Conway)
• Rectified tesseract (Norman W. Johnson)
• Rectified 4-hypercube
• Rectified 8-cell
• Rectified octachoron
• Rectified 4-measure polytope
• Rectified 4-regular orthotope
• Runcic tesseract (Norman W. Johnson)
• Runcic 4-hypercube
• Runcic 8-cell
• Runcic octachoron
• Runcic 4-measure polytope
• Runcic 4-regular orthotope