
Order-3 heptagonal tiling
Encyclopedia
In geometry
, the order-3 heptagonal tiling is a regular tiling of the hyperbolic plane
. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.

Heptagonal tiling (black lines) in a Poincaré half-plane model
The dual tiling is the order-7 triangular tiling.
there are eight hyperbolic uniform tilings
that can be based from the regular heptagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.

The symmetry group of the tiling is the (2,3,7) triangle group
, and a fundamental domain for this action is the (2,3,7) Schwarz triangle
. This is the smallest hyperbolic Schwarz triangle, and thus, by the proof of Hurwitz's automorphisms theorem, the tiling is the universal tiling that covers all Hurwitz surface
s (the Riemann surfaces with maximal symmetry group), giving them a tiling by hepatgons whose symmetry group equals their automorphism group as Riemann surfaces. The smallest Hurwitz surface is the Klein quartic
(genus 3, automorphism group of order 168), and the induced tiling has 24 heptagons, meeting at 56 vertices.
The dual order-7 triangular tiling has the same symmetry group, and thus yields triangulations of Hurwitz surfaces.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the order-3 heptagonal tiling is a regular tiling of the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.
Images

Heptagonal tiling (black lines) in a Poincaré half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
Related polyhedra and tilings
This tiling is topologically related as a part of sequence of regular polyhedra with Schl%C3%A4fli symbol {n,3}. {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 {4,3} Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {9,3} |
(∞,3} |
The dual tiling is the order-7 triangular tiling.
 order-3 heptagonal tiling |
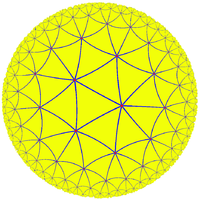 order-7 triangular tiling |
Wythoff constructions from heptagonal and triangular tilings
From a Wythoff constructionWythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
there are eight hyperbolic uniform tilings
Uniform tilings in hyperbolic plane
There are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
that can be based from the regular heptagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.
| Tiling | Schläfli symbol |
Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
Image |
|---|---|---|---|---|
| Order-3 heptagonal tiling | t0{7,3} | 3 | 7 2 | 73 |  |
| Order-3 truncated heptagonal tiling Order-3 truncated heptagonal tiling In geometry, the Truncated order-3 heptagonal tiling is a semiregular tiling of the hyperbolic plane. There is one triangle and two tetrakaidecagons on each vertex... |
t0,1{7,3} | 2 3 | 7 | 3.14.14 |  |
| Rectified order-3 heptagonal tiling (Triheptagonal tiling Triheptagonal tiling In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex... ) |
t1{7,3} | 2 | 7 3 | (3.7)2 |  |
| Bitruncated order-3 heptagonal tiling (Order-7 truncated triangular tiling Order-7 truncated triangular tiling In geometry, the Order 7 truncated heptagonal tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball with heptagons in place of pentagons... ) |
t1,2{7,3} | 2 7 | 3 | 7.6.6 |  |
| Order-7 triangular tiling | t2{7,3} | 7 | 3 2 | 37 |  |
| Cantellated order-3 heptagonal tiling (Rhombitriheptagonal tiling) |
t0,2{7,3} | 7 3 | 2 | 3.4.7.4 |  |
| Order-3 omnitruncated heptagonal tiling (Truncated triheptagonal tiling) |
t0,1,2{7,3} | 7 3 2 | | 4.7.14 | 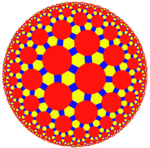 |
| Order-3 snub heptagonal tiling | s{7,3} | | 7 3 2 | 3.3.3.3.7 |  |
Hurwitz surfaces

The symmetry group of the tiling is the (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
, and a fundamental domain for this action is the (2,3,7) Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
. This is the smallest hyperbolic Schwarz triangle, and thus, by the proof of Hurwitz's automorphisms theorem, the tiling is the universal tiling that covers all Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
s (the Riemann surfaces with maximal symmetry group), giving them a tiling by hepatgons whose symmetry group equals their automorphism group as Riemann surfaces. The smallest Hurwitz surface is the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
(genus 3, automorphism group of order 168), and the induced tiling has 24 heptagons, meeting at 56 vertices.
The dual order-7 triangular tiling has the same symmetry group, and thus yields triangulations of Hurwitz surfaces.
See also
- Hexagonal tiling
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes

