
Quantum potential
Encyclopedia
The quantum potential is a central concept of the de Broglie–Bohm formulation of quantum mechanics
, introduced by David Bohm
in 1952.
Initially presented under the name quantum-mechanical potential, subsequently quantum potential, it was later elaborated upon by Bohm and Basil Hiley
in its interpretation as an information potential which acts on a quantum particle. It is also referred to as quantum potential energy, Bohm potential, quantum Bohm potential or Bohm quantum potential.
In the framework of the de Broglie–Bohm theory, the quantum potential is a term within the Schrödinger equation
which acts to guide the movement of quantum particles. The quantum potential approach introduced by Bohm provides a formally more complete exposition of the idea presented by Louis de Broglie: de Broglie had postulated in 1926 that the wave function represents a pilot wave
which guides a quantum particle, but had subsequently abandoned his approach due to objections raised by Wolfgang Pauli
. The seminal articles of Bohm in 1952 introduced the quantum potential and included answers to the objections which had been raised against the pilot wave theory.
Building on the interpretation of the quantum theory introduced by Bohm in 1952, David Bohm and Basil Hiley
in 1975 presented how the concept of a quantum potential leads to the notion of an “unbroken wholeness of the entire universe”, proposing that the fundamental new quality introduced by quantum physics is nonlocality
.
, in its quantum potential formulation, is re-written as:
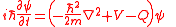
where is the quantum potential, defined as
is the quantum potential, defined as 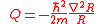
with wave function: and real-valued functions
and real-valued functions  and
and 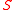 , where
, where  is the amplitude (absolute value
is the amplitude (absolute value
) of the wave function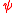 and
and  its phase. The quantum potential
its phase. The quantum potential  thus depends on the curvature of the amplitude of the wave function. (Compare also: derivation of the Schrödinger equation in pilot wave theory.)
thus depends on the curvature of the amplitude of the wave function. (Compare also: derivation of the Schrödinger equation in pilot wave theory.)
In the limit →0, the function
→0, the function  is a solution of the (classical) Hamilton-Jacobi equation; therefore, the function
is a solution of the (classical) Hamilton-Jacobi equation; therefore, the function  is also called the Hamilton-Jacobi function or action
is also called the Hamilton-Jacobi function or action
extended to quantum physics.
In 1979, Hiley and his co-workers Philippidis and Dewdney presented a full calculation on the explanation of the two-slit experiment in terms of Bohmian trajectories that arise for each particle moving under the influence of the quantum potential, resulting in the well-known interference patterns.
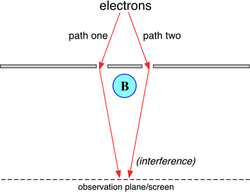 Also the shift of the interference pattern which occurs in presence of a magnetic field in the Aharonov-Bohm effect
Also the shift of the interference pattern which occurs in presence of a magnetic field in the Aharonov-Bohm effect
could be explained as arising from the quantum potential.
The collapse of the wave function of the Copenhagen interpretation of quantum theory is explained in the quantum potential approach by the demonstration that, after a measurement, “all the packets of the multi-dimensional wave function that do not correspond to the actual result of measurement have no effect on the particle” from then on. Bohm and Hiley pointed out that
Measurement then “involves a participatory transformation in which both the system under observation and the observing apparatus undergo a mutual participation so that the trajectories behave in a correlated manner, becoming correlated and separated into different, non-overlapping sets (which we call ‘channels’)”.
. Rather, it is represented in configuration space
, with three dimensions per particle. A single point in configuration space thus represents the configuration of the entire n-particle system as a whole.
A two-particle wave function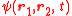 of identical particles of mass
of identical particles of mass  has the quantum potential
has the quantum potential
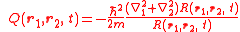
where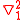 and
and 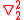 refer to particle 1 and particle 2 respectively.
refer to particle 1 and particle 2 respectively.
In case the wave function is separable, that is, if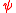 factorizes in the form
factorizes in the form 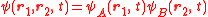 , then it follows that also
, then it follows that also  factorizes, and the system's total quantum potential becomes the sum of the quantum potentials of the two particles:
factorizes, and the system's total quantum potential becomes the sum of the quantum potentials of the two particles:
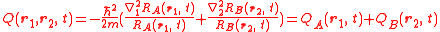
In this case, the two one-particle systems behave independently. More generally, the quantum potential of an -particle system with separable wave function is the sum of
-particle system with separable wave function is the sum of  quantum potentials, separating the system into
quantum potentials, separating the system into  independent one-particle systems.
independent one-particle systems.
Exact separability is extremely unphysical given that interactions between the system and its environment destroy the factorization. Yet a wave function that is a superposition
of several wave functions of approximately disjoint support
will approximately factorize.
, have sought to provide evidence that the Born rule
linking to the probability density function
to the probability density function

can be understood, in a pilot wave formulation, as not representing a basic law, but rather a theorem (called quantum equilibrium hypothesis) which applies when a quantum equilibrium is reached during the course of the time development under the Schrödinger equation. With Born's rule, and straightforward application of the chain
and product rule
s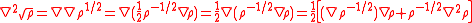
the quantum potential, expressed in terms of the probability density function, becomes:
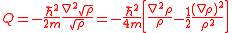
 , expressed in terms of the probability distribution, amounts to:
, expressed in terms of the probability distribution, amounts to: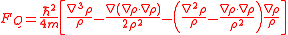
( -space), the quantum potential can also be formulated in terms of momentum space (
-space), the quantum potential can also be formulated in terms of momentum space (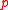 -space).
-space).
Hiley has shown that there exists complete symmetry between the -representation, and that the quantum potential as it appears in configuration space can be seen as arising from the dispersion of the momentum
-representation, and that the quantum potential as it appears in configuration space can be seen as arising from the dispersion of the momentum 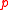 -representation. In algebraic terms, the quantum potential can be seen as arising from the relation between implicate and explicate orders
-representation. In algebraic terms, the quantum potential can be seen as arising from the relation between implicate and explicate orders
: if a non-commutative algebra is employed to describe the non-commutative structure of the quantum formalism, it turns out that it is impossible to define an underlying space, but that rather “shadow spaces” (homomorphic spaces) can be constructed and that in so doing the quantum potential appears.
The approach has been extended to phase space
, also in terms of a Duffin–Kemmer–Petiau algebra
approach.
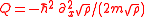 is proportional to the probability density's Fisher information
is proportional to the probability density's Fisher information
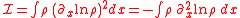 .
.
Alternatively,
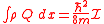
, the quantum potential can be identified with the kinetic energy
of the internal motion (“zitterbewegung
”) associated with the spin
of a spin-½
particle observed in a center-of-mass frame. More specifically, they showed that the internal zitterbewegung velocity for a spinning, non-relativistic particle of constant spin with no precession, and in absence of an external field, has the squared value:

from which the second term is shown to be of negligible size; then with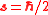 it follows that
it follows that
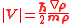
Salesi gave further details on this work in 2009.
In 1999, Salvatore Esposito generalized their result from spin-½ particles to particles of arbitrary spin, confirming the interpretation of the quantum potential as a kinetic energy for an internal motion. Esposito showed that (using the notation =1) the quantum potential can be written as:
=1) the quantum potential can be written as:
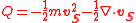
and that the causal interpretation of quantum mechanics can be reformulated in terms of a particle velocity

where the “drift velocity” is

and the “relative velocity” is , with
, with

and representing the spin direction of the particle. In this formulation, according to Esposito, quantum mechanics must necessarily be interpreted in probabilistic terms, for the reason that a system's initial motion condition cannot be exactly determined. Esposito explained that “the quantum effects present in the Schrödinger equation are due to the presence of a peculiar spatial direction associated with the particle that, assuming the isotropy of space, can be identified with the spin of the particle itself”. Esposito generalized it from matter particles to gauge particles
representing the spin direction of the particle. In this formulation, according to Esposito, quantum mechanics must necessarily be interpreted in probabilistic terms, for the reason that a system's initial motion condition cannot be exactly determined. Esposito explained that “the quantum effects present in the Schrödinger equation are due to the presence of a peculiar spatial direction associated with the particle that, assuming the isotropy of space, can be identified with the spin of the particle itself”. Esposito generalized it from matter particles to gauge particles
, in particular photon
s, for which he showed that, if modelled as , with probability function
, with probability function  , they can be understood in a quantum potential approach.
, they can be understood in a quantum potential approach.
James R. Bogan, in 2002, published the derivation of a reciprocal transformation from the Hamilton-Jacobi equation of classical mechanics to the time-dependent Schrödinger equation of quantum mechanics which arises from a gauge transformation representing spin, under the simple requirement of conservation of probability. This spin-dependent transformation is a function of the quantum potential.
formulate on the basis of an Equivalence Principle (EP), a quantum potential is written in terms of the Schwarzian derivative
 as:
as:

Even in cases where this equals

it is stressed by E. Faraggi and M. Matone that this does not correspond with the usual quantum potential, as in their approach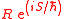 is a solution to the Schrödinger equation but does not correspond to the wave function. This has been investigated further by E.R. Floyd for the classical limit
is a solution to the Schrödinger equation but does not correspond to the wave function. This has been investigated further by E.R. Floyd for the classical limit 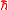 → 0, as well as by Robert Carroll.
→ 0, as well as by Robert Carroll.
, taking account of recent advances that include the work of David Hestenes
on spacetime algebra
. They show how, within a nested hierarchy of Clifford algebras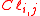 , for each Clifford algebra
, for each Clifford algebra
an element of a minimum left ideal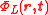 and an element of a right ideal representing its Clifford conjugation
and an element of a right ideal representing its Clifford conjugation 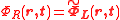 can be constructed, and from it the Clifford density element (CDE)
can be constructed, and from it the Clifford density element (CDE)  , an element of the Clifford algebra which is isomorphic to the standard density matrix
, an element of the Clifford algebra which is isomorphic to the standard density matrix
but independent of any specific representation. On this basis, bilinear variants can be formed which represent properties of the system. Hiley and Callaghan distinguish bilinear invariants of a first kind, of which each stands for the expectation value of an element of the algebra which can be formed as
of the algebra which can be formed as  , and bilinear invariants of a second kind which are constructed with derivatives, to represent momentum and energy. Using these terms, they reconstruct the results of quantum mechanics without depending on a particular representation in terms of a wave function nor requiring reference to an external Hilbert space. Consistent with earlier results, the quantum potential of a Pauli particle is shown to have an additional spin-dependent term, and the momentum of a Dirac particle is shown to consist in a linear motion and a rotational part. The two dynamical equations governing the time evolution are re-interpreted as conservation equations. One of them stands for the conservation of energy
, and bilinear invariants of a second kind which are constructed with derivatives, to represent momentum and energy. Using these terms, they reconstruct the results of quantum mechanics without depending on a particular representation in terms of a wave function nor requiring reference to an external Hilbert space. Consistent with earlier results, the quantum potential of a Pauli particle is shown to have an additional spin-dependent term, and the momentum of a Dirac particle is shown to consist in a linear motion and a rotational part. The two dynamical equations governing the time evolution are re-interpreted as conservation equations. One of them stands for the conservation of energy
; the other stands for the conservation of probability and spin. The quantum potential plays the role of an internal energy which ensures the conservation of total energy.
The quantum potential approach was extended by Hiley and co-workers to quantum field theory in Minkowski space
time and to curved spacetime.
Carlo Castro and Jorge Mahecha derived the Schrödinger equation from the Hamilton-Jacobi equation in conjunction with the continuity equation, and showed that the properties of the relativistic Bohm quantum potential in terms of the ensemble density can be described by the Weyl properties of space. In Riemann flat space, the Bohm potential is shown to equal the Weyl curvature. According to Castro and Mahecha, in the relativistic case
, the quantum potential (using the d'Alembert operator
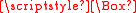 and in the notation
and in the notation  ) takes the form
) takes the form
and the quantum force exerced by the relativistic quantum potential is shown to depend on the Weyl gauge potential and its derivatives. Furthermore, the relationship among Bohm’s potential and the Weyl curvature in flat spacetime corresponds to a similar relationship among Fisher Information and Weyl geometry after introduction of a complex
momentum.
Diego L. Rapoport, on the other hand, associates the relativistic quantum potential with the metric scalar curvature (Riemann curvature).
In relation to the Klein-Gordon equation for a particle with mass and charge, Peter R. Holland spoke in his book of 1993 of a ‘quantum potential-like term’ that is proportional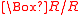 . He emphasized however that to give the Klein-Gordon theory a single-particle interpretation in terms of trajectories, as can be done for nonrelativistic Schrödinger quantum mechanics, would lead to unacceptable inconsistencies. For instance, wave functions
. He emphasized however that to give the Klein-Gordon theory a single-particle interpretation in terms of trajectories, as can be done for nonrelativistic Schrödinger quantum mechanics, would lead to unacceptable inconsistencies. For instance, wave functions  that are solutions to the Klein-Gordon or the Dirac equation
that are solutions to the Klein-Gordon or the Dirac equation
cannot be interpreted as the probability amplitude for a particle to be found in a given volume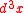 at time
at time  in accordance with the usual axioms of quantum mechanics, and similarly in the causal interpretation it cannot be interpreted as the probability for the particle to be in that volume at that time. Holland pointed out that, while efforts have been made to determine a Hermitian position operator that would allow an interpretation of configuration space quantum field theory, in particular using the Newton–Wigner localization approach, but that no connection with possibilities for an empirical determination of position in terms of a relativistic measurement theory or for a trajectory interpretation has so far been established. Yet according to Holland this does not mean that the trajectory concept is to be discarded from considerations of relativistic quantum mechanics.
in accordance with the usual axioms of quantum mechanics, and similarly in the causal interpretation it cannot be interpreted as the probability for the particle to be in that volume at that time. Holland pointed out that, while efforts have been made to determine a Hermitian position operator that would allow an interpretation of configuration space quantum field theory, in particular using the Newton–Wigner localization approach, but that no connection with possibilities for an empirical determination of position in terms of a relativistic measurement theory or for a trajectory interpretation has so far been established. Yet according to Holland this does not mean that the trajectory concept is to be discarded from considerations of relativistic quantum mechanics.
Hrvoje Nikolić derived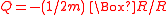 as expression for the quantum potential, and he proposed a Lorentz-covariant formulation of the Bohmian interpretation of many-particle wave functions. He also developed a generalized relativistic-invariant probabilistic interpretation of quantum theory, in which
as expression for the quantum potential, and he proposed a Lorentz-covariant formulation of the Bohmian interpretation of many-particle wave functions. He also developed a generalized relativistic-invariant probabilistic interpretation of quantum theory, in which 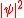 is no longer a probability density in space but a probability density in space-time.
is no longer a probability density in space but a probability density in space-time.
 , with
, with  real-valued functional
real-valued functional
s, can be shown to lead to
This has been called the superquantum potential by Bohm and his co-workers.
Basil Hiley showed that the energy-momentum-relations in the Bohm model can be obtained directly from the energy-momentum tensor of quantum field theory
and that the quantum potential is an energy term that is required for local energy-momentum conservation.
, Bohm already spoke of a “quantum-mechanical” potential.
Basil and Hiley also called the quantum potential an information potential, given that it influences the form of processes and is itself shaped by the environment. Bohm indicated “The ship or aeroplane (with its automatic Pilot) is a self-active system, i.e. it has its own energy. But the form of its activity is determined by the information content concerning its environment that is carried by the radar waves. This is independent of the intensity of the waves. We can similarly regard the quantum potential as containing active information. It is potentially active everywhere, but actually active only where and when there is a particle.” (italics in original).
Hiley has emphasized that the quantum potential, for Bohm, was “a key element in gaining insights into what could underlie the quantum formalism. It was his deeper analysis of this aspect of the approach that convinced him that the theory could not be mechanical. Rather it was organic in the sense of Whitehead
. Namely, that it was the whole that determined the properties of the individual particles and their relationship, not the other way round.”
Peter R. Holland
, in his comprehensive textbook, also refers to it as quantum potential energy. The quantum potential is also referred to in association with Bohm's name as Bohm potential, quantum Bohm potential or Bohm quantum potential.
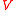 and
and  , and the resulting divergence of the velocity field determines the change to the density.
, and the resulting divergence of the velocity field determines the change to the density.
The approach using Bohmian trajectories and the quantum potential is used for calculating properties of quantum systems which cannot be solved exactly, which are often approximated using semi-classical approaches. Whereas in mean field approaches
the potential for the classical motion results from an average over wave functions, this approach does not require the computation of an integral over wave functions.
The expression for the quantum force has been used, together with Bayesian statistical analysis
and Expectation-maximisation methods, for computing ensembles of trajectories that arise under the influence of classical and quantum forces.
Recent articles:
Overview:
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, introduced by David Bohm
David Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
in 1952.
Initially presented under the name quantum-mechanical potential, subsequently quantum potential, it was later elaborated upon by Bohm and Basil Hiley
Basil Hiley
Basil Hiley, born 1935, is a British quantum physicist and professor emeritus of the University of London.- Work :Hiley published a paper in 1961 on the random walk of a macromolecule, which was followed by further papers on the Ising model, and lattice constant systems defined in graph theoretical...
in its interpretation as an information potential which acts on a quantum particle. It is also referred to as quantum potential energy, Bohm potential, quantum Bohm potential or Bohm quantum potential.
In the framework of the de Broglie–Bohm theory, the quantum potential is a term within the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
which acts to guide the movement of quantum particles. The quantum potential approach introduced by Bohm provides a formally more complete exposition of the idea presented by Louis de Broglie: de Broglie had postulated in 1926 that the wave function represents a pilot wave
Pilot wave
In theoretical physics, the Pilot Wave theory was the first known example of a hidden variable theory, presented by Louis de Broglie in 1927. Its more modern version, the Bohm interpretation,...
which guides a quantum particle, but had subsequently abandoned his approach due to objections raised by Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
. The seminal articles of Bohm in 1952 introduced the quantum potential and included answers to the objections which had been raised against the pilot wave theory.
| Quantum potential |
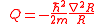 |
Building on the interpretation of the quantum theory introduced by Bohm in 1952, David Bohm and Basil Hiley
Basil Hiley
Basil Hiley, born 1935, is a British quantum physicist and professor emeritus of the University of London.- Work :Hiley published a paper in 1961 on the random walk of a macromolecule, which was followed by further papers on the Ising model, and lattice constant systems defined in graph theoretical...
in 1975 presented how the concept of a quantum potential leads to the notion of an “unbroken wholeness of the entire universe”, proposing that the fundamental new quality introduced by quantum physics is nonlocality
Quantum nonlocality
Quantum nonlocality is the phenomenon by which measurements made at a microscopic level necessarily refute one or more notions that are regarded as intuitively true in classical mechanics...
.
Quantum potential as part of the Schrödinger equation
The Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, in its quantum potential formulation, is re-written as:
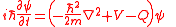
where
 is the quantum potential, defined as
is the quantum potential, defined as 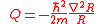
with wave function:
 and real-valued functions
and real-valued functions  and
and 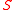 , where
, where  is the amplitude (absolute value
is the amplitude (absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
) of the wave function
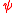 and
and  its phase. The quantum potential
its phase. The quantum potential  thus depends on the curvature of the amplitude of the wave function. (Compare also: derivation of the Schrödinger equation in pilot wave theory.)
thus depends on the curvature of the amplitude of the wave function. (Compare also: derivation of the Schrödinger equation in pilot wave theory.)In the limit
 →0, the function
→0, the function 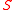 is a solution of the (classical) Hamilton-Jacobi equation; therefore, the function
is a solution of the (classical) Hamilton-Jacobi equation; therefore, the function 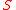 is also called the Hamilton-Jacobi function or action
is also called the Hamilton-Jacobi function or actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
extended to quantum physics.
Properties
Hiley emphasised three aspects that regard the quantum potential of a quantum particle:- it is real-valued, derived mathematically from the wave function and not from a Hamiltonian or other external source, and could be said to be involved in a self-organising processSelf-organizationSelf-organization is the process where a structure or pattern appears in a system without a central authority or external element imposing it through planning...
involving a basic underlying field; - it does not change if
 is multiplied by a constant, as this term is also present in the denominator, so that
is multiplied by a constant, as this term is also present in the denominator, so that  is independent of the magnitude of
is independent of the magnitude of  and thus of field intensity; therefore, the quantum potential fulfils a precondition for nonlocality: it need not fall off as distance increases;
and thus of field intensity; therefore, the quantum potential fulfils a precondition for nonlocality: it need not fall off as distance increases; - it carries information about the whole experimental arrangement in which the particle finds itself.
In 1979, Hiley and his co-workers Philippidis and Dewdney presented a full calculation on the explanation of the two-slit experiment in terms of Bohmian trajectories that arise for each particle moving under the influence of the quantum potential, resulting in the well-known interference patterns.

Aharonov-Bohm effect
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–Bohm effect, is a quantum mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic field , despite being confined to a region in which both the magnetic field B and electric field E are...
could be explained as arising from the quantum potential.
The collapse of the wave function of the Copenhagen interpretation of quantum theory is explained in the quantum potential approach by the demonstration that, after a measurement, “all the packets of the multi-dimensional wave function that do not correspond to the actual result of measurement have no effect on the particle” from then on. Bohm and Hiley pointed out that
- ‘the quantum potential can develop unstable bifurcation points, which separate classes of particle trajectories according to the “channels” into which they eventually enter and within which they stay. This explains how measurement is possible without “collapse” of the wave function, and how all sorts of quantum processes, such as transitions between states, fusion of two states into one and fission of one system into two, are able to take place without the need for a human observer.’
Measurement then “involves a participatory transformation in which both the system under observation and the observing apparatus undergo a mutual participation so that the trajectories behave in a correlated manner, becoming correlated and separated into different, non-overlapping sets (which we call ‘channels’)”.
Quantum potential of an n-particle system
The Schrödinger wave function of a many-particle quantum system cannot be represented in ordinary three-dimensional spaceThree-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
. Rather, it is represented in configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
, with three dimensions per particle. A single point in configuration space thus represents the configuration of the entire n-particle system as a whole.
A two-particle wave function
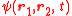 of identical particles of mass
of identical particles of mass  has the quantum potential
has the quantum potential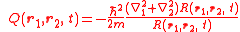
where
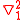 and
and 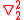 refer to particle 1 and particle 2 respectively.
refer to particle 1 and particle 2 respectively.In case the wave function is separable, that is, if
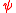 factorizes in the form
factorizes in the form 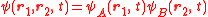 , then it follows that also
, then it follows that also  factorizes, and the system's total quantum potential becomes the sum of the quantum potentials of the two particles:
factorizes, and the system's total quantum potential becomes the sum of the quantum potentials of the two particles: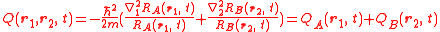
In this case, the two one-particle systems behave independently. More generally, the quantum potential of an
 -particle system with separable wave function is the sum of
-particle system with separable wave function is the sum of  quantum potentials, separating the system into
quantum potentials, separating the system into  independent one-particle systems.
independent one-particle systems.Exact separability is extremely unphysical given that interactions between the system and its environment destroy the factorization. Yet a wave function that is a superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of several wave functions of approximately disjoint support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
will approximately factorize.
Quantum potential in terms of the probability density function
Bohm, as well as other physicists after him including Antony ValentiniAntony Valentini
Antony Valentini is a theoretical physicist and a professor at Clemson University. He is known for his work on the foundations of quantum physics.- Education and career :...
, have sought to provide evidence that the Born rule
Born rule
The Born rule is a law of quantum mechanics which gives the probability that a measurement on a quantum system will yield a given result. It is named after its originator, the physicist Max Born. The Born rule is one of the key principles of quantum mechanics...
linking
 to the probability density function
to the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

can be understood, in a pilot wave formulation, as not representing a basic law, but rather a theorem (called quantum equilibrium hypothesis) which applies when a quantum equilibrium is reached during the course of the time development under the Schrödinger equation. With Born's rule, and straightforward application of the chain
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
s
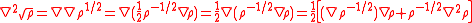
the quantum potential, expressed in terms of the probability density function, becomes:
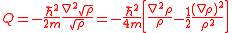
Quantum force
The quantum force , expressed in terms of the probability distribution, amounts to:
, expressed in terms of the probability distribution, amounts to: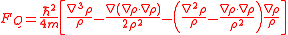
Formulation in configuration space and in momentum space
M. R. Brown and B. Hiley showed that, as alternative to its formulation terms of configuration spaceConfiguration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
(
 -space), the quantum potential can also be formulated in terms of momentum space (
-space), the quantum potential can also be formulated in terms of momentum space (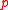 -space).
-space).Hiley has shown that there exists complete symmetry between the
 -representation, and that the quantum potential as it appears in configuration space can be seen as arising from the dispersion of the momentum
-representation, and that the quantum potential as it appears in configuration space can be seen as arising from the dispersion of the momentum  -representation. In algebraic terms, the quantum potential can be seen as arising from the relation between implicate and explicate orders
-representation. In algebraic terms, the quantum potential can be seen as arising from the relation between implicate and explicate ordersImplicate and explicate order according to David Bohm
According to David Bohm's theory, implicate and explicate orders are characterised by:-David Bohm's challenges to some generally prevailing views:...
: if a non-commutative algebra is employed to describe the non-commutative structure of the quantum formalism, it turns out that it is impossible to define an underlying space, but that rather “shadow spaces” (homomorphic spaces) can be constructed and that in so doing the quantum potential appears.
The approach has been extended to phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
, also in terms of a Duffin–Kemmer–Petiau algebra
Duffin–Kemmer–Petiau algebra
In mathematical physics, the Duffin–Kemmer–Petiau algebra , introduced by R.J. Duffin, Nicholas Kemmer and G. Petiau, is the algebra which is generated by the Duffin–Kemmer–Petiau matrices...
approach.
Relation to the Fisher information
It can be shown that the mean value of the quantum potential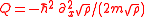 is proportional to the probability density's Fisher information
is proportional to the probability density's Fisher informationFisher information
In mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
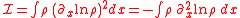 .
.Alternatively,
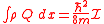
Quantum potential as internal motion associated with spin
Givanni Salesi, Erasmo Recami and co-workers showed in 1998 that, in agreement with the König's theoremKönig's theorem (kinetics)
Konig's theorem is related to kinetics of a system of particles.- The theorem :It states that the kinetic energy of a system of particles is the kinetic energy associated to the movement of the center of mass and the kinetic energy associated to the movement of the particles relative to the center...
, the quantum potential can be identified with the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the internal motion (“zitterbewegung
Zitterbewegung
Zitterbewegung is a theoretical rapid motion of elementary particles, in particular electrons, that obey the Dirac equation...
”) associated with the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of a spin-½
Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
particle observed in a center-of-mass frame. More specifically, they showed that the internal zitterbewegung velocity for a spinning, non-relativistic particle of constant spin with no precession, and in absence of an external field, has the squared value:

from which the second term is shown to be of negligible size; then with
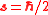 it follows that
it follows that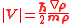
Salesi gave further details on this work in 2009.
In 1999, Salvatore Esposito generalized their result from spin-½ particles to particles of arbitrary spin, confirming the interpretation of the quantum potential as a kinetic energy for an internal motion. Esposito showed that (using the notation
 =1) the quantum potential can be written as:
=1) the quantum potential can be written as: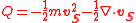
and that the causal interpretation of quantum mechanics can be reformulated in terms of a particle velocity

where the “drift velocity” is

and the “relative velocity” is
 , with
, with
and
 representing the spin direction of the particle. In this formulation, according to Esposito, quantum mechanics must necessarily be interpreted in probabilistic terms, for the reason that a system's initial motion condition cannot be exactly determined. Esposito explained that “the quantum effects present in the Schrödinger equation are due to the presence of a peculiar spatial direction associated with the particle that, assuming the isotropy of space, can be identified with the spin of the particle itself”. Esposito generalized it from matter particles to gauge particles
representing the spin direction of the particle. In this formulation, according to Esposito, quantum mechanics must necessarily be interpreted in probabilistic terms, for the reason that a system's initial motion condition cannot be exactly determined. Esposito explained that “the quantum effects present in the Schrödinger equation are due to the presence of a peculiar spatial direction associated with the particle that, assuming the isotropy of space, can be identified with the spin of the particle itself”. Esposito generalized it from matter particles to gauge particlesGauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
, in particular photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, for which he showed that, if modelled as
 , with probability function
, with probability function  , they can be understood in a quantum potential approach.
, they can be understood in a quantum potential approach.James R. Bogan, in 2002, published the derivation of a reciprocal transformation from the Hamilton-Jacobi equation of classical mechanics to the time-dependent Schrödinger equation of quantum mechanics which arises from a gauge transformation representing spin, under the simple requirement of conservation of probability. This spin-dependent transformation is a function of the quantum potential.
EP quantum mechanics with quantum potential as Schwarzian derivative
In a different approach, the EP quantum mechanicsEP Quantum Mechanics
In physics, EP quantum mechanics is a theory of motion of point particles, partly included in the framework of quantum trajectory representation theories of quantum mechanics, based upon an equivalence postulate similar in content to the equivalence principle of general relativity, rather than on...
formulate on the basis of an Equivalence Principle (EP), a quantum potential is written in terms of the Schwarzian derivative
Schwarzian derivative
In mathematics, the Schwarzian derivative, named after the German mathematician Hermann Schwarz, is a certain operator that is invariant under all linear fractional transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and...
 as:
as:
Even in cases where this equals

it is stressed by E. Faraggi and M. Matone that this does not correspond with the usual quantum potential, as in their approach
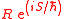 is a solution to the Schrödinger equation but does not correspond to the wave function. This has been investigated further by E.R. Floyd for the classical limit
is a solution to the Schrödinger equation but does not correspond to the wave function. This has been investigated further by E.R. Floyd for the classical limit 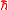 → 0, as well as by Robert Carroll.
→ 0, as well as by Robert Carroll.Re-interpretation in terms of Clifford algebras
B. Hiley and R. E. Callaghan re-interpret the role of the Bohm model and its notion of quantum potential in the framework of Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
, taking account of recent advances that include the work of David Hestenes
David Hestenes
David Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
on spacetime algebra
Spacetime algebra
In mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
. They show how, within a nested hierarchy of Clifford algebras
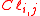 , for each Clifford algebra
, for each Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
an element of a minimum left ideal
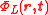 and an element of a right ideal representing its Clifford conjugation
and an element of a right ideal representing its Clifford conjugation 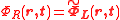 can be constructed, and from it the Clifford density element (CDE)
can be constructed, and from it the Clifford density element (CDE)  , an element of the Clifford algebra which is isomorphic to the standard density matrix
, an element of the Clifford algebra which is isomorphic to the standard density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
but independent of any specific representation. On this basis, bilinear variants can be formed which represent properties of the system. Hiley and Callaghan distinguish bilinear invariants of a first kind, of which each stands for the expectation value of an element
 of the algebra which can be formed as
of the algebra which can be formed as  , and bilinear invariants of a second kind which are constructed with derivatives, to represent momentum and energy. Using these terms, they reconstruct the results of quantum mechanics without depending on a particular representation in terms of a wave function nor requiring reference to an external Hilbert space. Consistent with earlier results, the quantum potential of a Pauli particle is shown to have an additional spin-dependent term, and the momentum of a Dirac particle is shown to consist in a linear motion and a rotational part. The two dynamical equations governing the time evolution are re-interpreted as conservation equations. One of them stands for the conservation of energy
, and bilinear invariants of a second kind which are constructed with derivatives, to represent momentum and energy. Using these terms, they reconstruct the results of quantum mechanics without depending on a particular representation in terms of a wave function nor requiring reference to an external Hilbert space. Consistent with earlier results, the quantum potential of a Pauli particle is shown to have an additional spin-dependent term, and the momentum of a Dirac particle is shown to consist in a linear motion and a rotational part. The two dynamical equations governing the time evolution are re-interpreted as conservation equations. One of them stands for the conservation of energyConservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
; the other stands for the conservation of probability and spin. The quantum potential plays the role of an internal energy which ensures the conservation of total energy.
Quantum potential and relativity
Bohm and Hiley demonstrated that the non-locality of quantum theory can be understood as limit case of a purely local theory, provided the transmission of active information is allowed to be greater than the speed of light, and that this limit case yields approximations to both quantum theory and relativity.The quantum potential approach was extended by Hiley and co-workers to quantum field theory in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
time and to curved spacetime.
Carlo Castro and Jorge Mahecha derived the Schrödinger equation from the Hamilton-Jacobi equation in conjunction with the continuity equation, and showed that the properties of the relativistic Bohm quantum potential in terms of the ensemble density can be described by the Weyl properties of space. In Riemann flat space, the Bohm potential is shown to equal the Weyl curvature. According to Castro and Mahecha, in the relativistic case
Relativistic wave equations
Before the creation of quantum field theory, physicists attempted to formulate versions of the Schrödinger equation which were compatible with special relativity...
, the quantum potential (using the d'Alembert operator
D'Alembert operator
In special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...
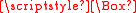 and in the notation
and in the notation  ) takes the form
) takes the form
and the quantum force exerced by the relativistic quantum potential is shown to depend on the Weyl gauge potential and its derivatives. Furthermore, the relationship among Bohm’s potential and the Weyl curvature in flat spacetime corresponds to a similar relationship among Fisher Information and Weyl geometry after introduction of a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
momentum.
Diego L. Rapoport, on the other hand, associates the relativistic quantum potential with the metric scalar curvature (Riemann curvature).
In relation to the Klein-Gordon equation for a particle with mass and charge, Peter R. Holland spoke in his book of 1993 of a ‘quantum potential-like term’ that is proportional
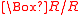 . He emphasized however that to give the Klein-Gordon theory a single-particle interpretation in terms of trajectories, as can be done for nonrelativistic Schrödinger quantum mechanics, would lead to unacceptable inconsistencies. For instance, wave functions
. He emphasized however that to give the Klein-Gordon theory a single-particle interpretation in terms of trajectories, as can be done for nonrelativistic Schrödinger quantum mechanics, would lead to unacceptable inconsistencies. For instance, wave functions  that are solutions to the Klein-Gordon or the Dirac equation
that are solutions to the Klein-Gordon or the Dirac equationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
cannot be interpreted as the probability amplitude for a particle to be found in a given volume
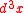 at time
at time  in accordance with the usual axioms of quantum mechanics, and similarly in the causal interpretation it cannot be interpreted as the probability for the particle to be in that volume at that time. Holland pointed out that, while efforts have been made to determine a Hermitian position operator that would allow an interpretation of configuration space quantum field theory, in particular using the Newton–Wigner localization approach, but that no connection with possibilities for an empirical determination of position in terms of a relativistic measurement theory or for a trajectory interpretation has so far been established. Yet according to Holland this does not mean that the trajectory concept is to be discarded from considerations of relativistic quantum mechanics.
in accordance with the usual axioms of quantum mechanics, and similarly in the causal interpretation it cannot be interpreted as the probability for the particle to be in that volume at that time. Holland pointed out that, while efforts have been made to determine a Hermitian position operator that would allow an interpretation of configuration space quantum field theory, in particular using the Newton–Wigner localization approach, but that no connection with possibilities for an empirical determination of position in terms of a relativistic measurement theory or for a trajectory interpretation has so far been established. Yet according to Holland this does not mean that the trajectory concept is to be discarded from considerations of relativistic quantum mechanics.Hrvoje Nikolić derived
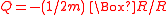 as expression for the quantum potential, and he proposed a Lorentz-covariant formulation of the Bohmian interpretation of many-particle wave functions. He also developed a generalized relativistic-invariant probabilistic interpretation of quantum theory, in which
as expression for the quantum potential, and he proposed a Lorentz-covariant formulation of the Bohmian interpretation of many-particle wave functions. He also developed a generalized relativistic-invariant probabilistic interpretation of quantum theory, in which 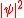 is no longer a probability density in space but a probability density in space-time.
is no longer a probability density in space but a probability density in space-time.Quantum potential in quantum field theory
Starting from the space representation of the field coordinate, a causal interpretation of the Schrödinger picture of relativistic quantum theory has been constructed starting from the space representation of the field coordinate. The Schrödinger picture for a neutral, spin 0, massless field , with
, with  real-valued functional
real-valued functionalFunctional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
s, can be shown to lead to

This has been called the superquantum potential by Bohm and his co-workers.
Basil Hiley showed that the energy-momentum-relations in the Bohm model can be obtained directly from the energy-momentum tensor of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and that the quantum potential is an energy term that is required for local energy-momentum conservation.
Interpretation and naming of the quantum potential
In his article of 1952, providing an alternative interpretation of quantum mechancsInterpretation of quantum mechanics
An interpretation of quantum mechanics is a set of statements which attempt to explain how quantum mechanics informs our understanding of nature. Although quantum mechanics has held up to rigorous and thorough experimental testing, many of these experiments are open to different interpretations...
, Bohm already spoke of a “quantum-mechanical” potential.
Basil and Hiley also called the quantum potential an information potential, given that it influences the form of processes and is itself shaped by the environment. Bohm indicated “The ship or aeroplane (with its automatic Pilot) is a self-active system, i.e. it has its own energy. But the form of its activity is determined by the information content concerning its environment that is carried by the radar waves. This is independent of the intensity of the waves. We can similarly regard the quantum potential as containing active information. It is potentially active everywhere, but actually active only where and when there is a particle.” (italics in original).
Hiley has emphasized that the quantum potential, for Bohm, was “a key element in gaining insights into what could underlie the quantum formalism. It was his deeper analysis of this aspect of the approach that convinced him that the theory could not be mechanical. Rather it was organic in the sense of Whitehead
Alfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
. Namely, that it was the whole that determined the properties of the individual particles and their relationship, not the other way round.”
Peter R. Holland
Peter R. Holland
Peter R. Holland is a theoretical physicist, known for his book on the pilot wave theory and the de Broglie-Bohm causal interpretation of quantum mechanics and his work on foundational problems in quantum physics....
, in his comprehensive textbook, also refers to it as quantum potential energy. The quantum potential is also referred to in association with Bohm's name as Bohm potential, quantum Bohm potential or Bohm quantum potential.
Applications
The quantum potential approach can be used to model quantum effects without requiring the Schrödinger equation to be explicitly solved, and it can be integrated in simulations, such as Monte Carlo simulations using the hydrodynamic and drift diffusion equations. This is done in form of a “hydrodynamic” calculation of trajectories: starting from the density at each “fluid element”, the acceleration of each “fluid element” is computed from the gradient of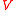 and
and  , and the resulting divergence of the velocity field determines the change to the density.
, and the resulting divergence of the velocity field determines the change to the density.The approach using Bohmian trajectories and the quantum potential is used for calculating properties of quantum systems which cannot be solved exactly, which are often approximated using semi-classical approaches. Whereas in mean field approaches
Mean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
the potential for the classical motion results from an average over wave functions, this approach does not require the computation of an integral over wave functions.
The expression for the quantum force has been used, together with Bayesian statistical analysis
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
and Expectation-maximisation methods, for computing ensembles of trajectories that arise under the influence of classical and quantum forces.
Further reading
Fundamental articles: (full text) (full text)- D. Bohm, B. J. Hiley, P. N. Kaloyerou: An ontological basis for the quantum theory, Physics Reports (Review section of Physics Letters), volume 144, number 6, pp. 321–375, 1987 (full text), therein: D. Bohm, B. J. Hiley: I. Non-relativistic particle systems, pp. 321–348, and D. Bohm, B. J. Hiley, P. N. Kaloyerou: II. A causal interpretation of quantum fields, pp. 349–375
Recent articles:
- Robert Carroll: Fluctuations, gravity, and the quantum potential, 13 January 2005, asXiv:gr-qc/0501045v1
Overview:
- Peter R. HollandPeter R. HollandPeter R. Holland is a theoretical physicist, known for his book on the pilot wave theory and the de Broglie-Bohm causal interpretation of quantum mechanics and his work on foundational problems in quantum physics....
: The Quantum Theory of Motion: An Account of the De Broglie-Bohm Causal Interpretation of Quantum Mechanics, Cambridge University Press, Cambridge (first published June 25 1993), ISBN 0-521-35404-8 hardback, ISBN 0-521-48543-6 paperback, transferred to digital printing 2004 - David BohmDavid BohmDavid Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
, Basil HileyBasil HileyBasil Hiley, born 1935, is a British quantum physicist and professor emeritus of the University of London.- Work :Hiley published a paper in 1961 on the random walk of a macromolecule, which was followed by further papers on the Ising model, and lattice constant systems defined in graph theoretical...
: The Undivided Universe: An Ontological Interpretation of Quantum Theory, Routledge, 1993, ISBN 0-415-06588-7 - David Bohm, F. David PeatF. David PeatF. David Peat was born in Waterloo, England and is a holistic physicist and author who has carried out research in solid state physics and the foundation of quantum theory....
: Science, Order and Creativity, 1987, Routledge, 2nd ed. 2000 (transferred to digital printing 2008, Routledge), ISBN 0-415-17182-2

