Pilot wave
Encyclopedia
In theoretical physics
, the Pilot Wave theory was the first known example of a hidden variable theory
, presented by Louis de Broglie in 1927. Its more modern version, the Bohm interpretation
,
remains a controversial attempt to interpret quantum mechanics
as a deterministic theory, avoiding
troublesome notions such as instantaneous wavefunction collapse
and the paradox of Schrödinger's cat
.
also supported by the current experimental evidence to the same extent as the other interpretations.
. Consequently:
The position and momentum of every particle are considered hidden variables; they are defined at all
times, but not known by the observer; the initial conditions of the particles are not known accurately, so
that from the point of view of the observer, there are uncertainties in the particles' states which conform to Heisenberg's Uncertainty Principle.
A collection of particles has an associated wave, which evolves according to the Schrödinger Equation
. Each of the particles follows a deterministic (but probably chaotic) trajectory, which is guided by the
wave function; collectively, the density of the particles conform to the magnitude of the wave function. The wave function is not influenced by the particle and can exist also as empty wave function.
In common with most interpretations of quantum mechanics other than the Many-worlds interpretation
, this theory has nonlocality
.
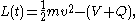
where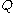
is the potential associated with the quantum force (the particle being pushed by the wave function),
is integrated along precisely one path (the one the electron actually follows).
This leads to the following formula for the Bohm propagator: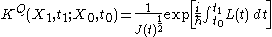
.
This propagator allows to track the electron precisely over time under the influence of the quantum potential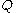
.
or Hamiltonian dynamics. Using the Hamilton-Jacobi equation
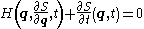
it is possible to derive the Schrödinger equation
:
Consider a classical particle — the position of which is not known with certainty. We must deal with it statistically, so only the probability density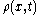
is known. Probability must be conserved, i.e. 
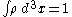for each 
. Therefore it must satisfy the continuity equation
where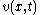
is the velocity of the particle.
In the Hamilton-Jacobi formulation of classical mechanics
, velocity is given by
where 
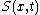is a solution of the Hamilton-Jacobi equation
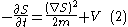
We can combine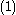
and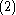 
into a single complex equation by introducing the complex function 
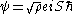, then the two equations are equivalent to
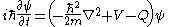with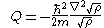 
This is the time dependent Schrödinger equation with an extra potential, the quantum potential
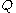, which is the potential of the quantum force, which is proportional (in approximation) to the curvature of the amplitude of the wavefunction.
and J. S. Bell
have emphasized that in the de Broglie–Bohm picture of quantum mechanics there can exist empty waves, represented by wave functions propagating in space and time but not carrying energy or momentum, and not associated with a particle. The same concept was called ghost waves (or “Gespensterfelder”, ghost fields) by Albert Einstein
.
The empty wave function notion has been discussed controversially. In contrast, the many-worlds interpretation of quantum mechanics does not call for empty wave functions.
suggested that the wave function of Schrödinger's wave equation represents the probability density of finding a particle.
From this idea, de Broglie developed the Pilot Wave theory, and worked out a function for the guiding wave. He presented the Pilot Wave theory at the 1927 Solvay Conference. However, Wolfgang Pauli
raised an objection to it at the conference, saying that it did not deal properly with the case of inelastic scattering
. De Broglie was not able to find a response to this objection, and he and Born abandoned the pilot-wave approach.
Later, in 1932, John von Neumann
published a paper claiming to prove that all hidden variable theories were impossible. (A result found to be flawed by Grete Hermann
three years later, though this went unnoticed by the physics community for over fifty years). However, in 1952, David Bohm
, dissatisfied with the prevailing orthodoxy, rediscovered de Broglie's Pilot Wave theory. Bohm developed Pilot Wave Theory into what is now called the De Broglie-Bohm theory.
The de Broglie-Bohm theory itself might have gone unnoticed by most physicists, if it had not been championed by John Bell
, who also countered the objections to it. In 1987, John Bell rediscovered Grete Hermann's work, and thus showed the physics community that Pauli's and von Neumann's objections really only showed that the Pilot Wave theory did not have locality; in fact, no quantum-mechanical theories have locality, so these objections did not invalidate the Pilot Wave theory.
The de Broglie-Bohm theory is now considered by some to be a valid challenge to the prevailing orthodoxy of the Copenhagen Interpretation
, but it remains controversial.
Yves Couder and co-workers recently discovered a macroscopic pilot wave system in the form of walking droplets. This system exhibits behaviour of a pilot wave, heretofore considered to be reserved to microscopic phenomena.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Pilot Wave theory was the first known example of a hidden variable theory
Hidden variable theory
Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation...
, presented by Louis de Broglie in 1927. Its more modern version, the Bohm interpretation
Bohm interpretation
The de Broglie–Bohm theory, also called the pilot-wave theory, Bohmian mechanics, and the causal interpretation, is an interpretation of quantum theory. In addition to a wavefunction on the space of all possible configurations, it also includes an actual configuration, even in situations where...
,
remains a controversial attempt to interpret quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
as a deterministic theory, avoiding
troublesome notions such as instantaneous wavefunction collapse
Wavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
and the paradox of Schrödinger's cat
Schrödinger's cat
Schrödinger's cat is a thought experiment, usually described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be...
.
The Pilot Wave theory
The Pilot Wave theory is one of several interpretations of Quantum Mechanics. It uses the same mathematics as other interpretations of quantum mechanics; consequently, it isalso supported by the current experimental evidence to the same extent as the other interpretations.
Principles
The Pilot Wave theory is a hidden variable theoryHidden variable theory
Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation...
. Consequently:
- the theory has realism (meaning that its concepts exist independently of the observer);
- the theory has determinismDeterminismDeterminism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
.
The position and momentum of every particle are considered hidden variables; they are defined at all
times, but not known by the observer; the initial conditions of the particles are not known accurately, so
that from the point of view of the observer, there are uncertainties in the particles' states which conform to Heisenberg's Uncertainty Principle.
A collection of particles has an associated wave, which evolves according to the Schrödinger Equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. Each of the particles follows a deterministic (but probably chaotic) trajectory, which is guided by the
wave function; collectively, the density of the particles conform to the magnitude of the wave function. The wave function is not influenced by the particle and can exist also as empty wave function.
In common with most interpretations of quantum mechanics other than the Many-worlds interpretation
Many-worlds interpretation
The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...
, this theory has nonlocality
Nonlocality
In Classical physics, nonlocality is the direct influence of one object on another, distant object. In Quantum mechanics, nonlocality refers to the absence of a local, realist model in agreement with quantum mechanical predictions.Nonlocality may refer to:...
.
Consequences
The Pilot Wave Theory shows that it is possible to have a theory that is realistic and deterministic, but still predicts the experimental results of Quantum Mechanics.Mathematical foundation
To derive the de Broglie-Bohm pilot-wave for an electron, the quantum Lagrangian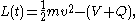where
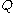is the potential associated with the quantum force (the particle being pushed by the wave function),is integrated along precisely one path (the one the electron actually follows).
This leads to the following formula for the Bohm propagator:
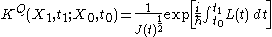.This propagator allows to track the electron precisely over time under the influence of the quantum potential
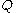.Derivation of the Schrödinger equation
Pilot Wave theory is based on Hamilton–Jacobi dynamics rather than LagrangianLagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
or Hamiltonian dynamics. Using the Hamilton-Jacobi equation
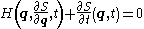
it is possible to derive the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
:
Consider a classical particle — the position of which is not known with certainty. We must deal with it statistically, so only the probability density
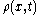is known. Probability must be conserved, i.e. 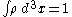for each . Therefore it must satisfy the continuity equationwhere
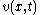is the velocity of the particle.In the Hamilton-Jacobi formulation of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, velocity is given by
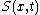where is a solution of the Hamilton-Jacobi equation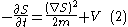We can combine
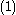and 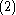into a single complex equation by introducing the complex function 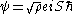, then the two equations are equivalent to 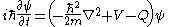with 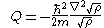This is the time dependent Schrödinger equation with an extra potential, the quantum potential
Quantum potential
The quantum potential is a central concept of the de Broglie–Bohm formulation of quantum mechanics, introduced by David Bohm in 1952.Initially presented under the name quantum-mechanical potential, subsequently quantum potential, it was later elaborated upon by Bohm and Basil Hiley in its...
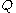, which is the potential of the quantum force, which is proportional (in approximation) to the curvature of the amplitude of the wavefunction.Empty wave function
Lucien HardyLucien Hardy
Lucien Hardy is a theoretical physicist, known for his work on the foundation of quantum physics including Hardy's paradox, a thought experiment he devised in 1992....
and J. S. Bell
John Stewart Bell
John Stewart Bell FRS was a British physicist from Northern Ireland , and the originator of Bell's theorem, a significant theorem in quantum physics regarding hidden variable theories.- Early life and work :...
have emphasized that in the de Broglie–Bohm picture of quantum mechanics there can exist empty waves, represented by wave functions propagating in space and time but not carrying energy or momentum, and not associated with a particle. The same concept was called ghost waves (or “Gespensterfelder”, ghost fields) by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
.
The empty wave function notion has been discussed controversially. In contrast, the many-worlds interpretation of quantum mechanics does not call for empty wave functions.
History
In his 1926 paper, Max BornMax Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
suggested that the wave function of Schrödinger's wave equation represents the probability density of finding a particle.
From this idea, de Broglie developed the Pilot Wave theory, and worked out a function for the guiding wave. He presented the Pilot Wave theory at the 1927 Solvay Conference. However, Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
raised an objection to it at the conference, saying that it did not deal properly with the case of inelastic scattering
Inelastic scattering
In particle physics and chemistry, inelastic scattering is a fundamental scattering process in which the kinetic energy of an incident particle is not conserved . In an inelastic scattering process, some of the energy of the incident particle is lost or gained...
. De Broglie was not able to find a response to this objection, and he and Born abandoned the pilot-wave approach.
Later, in 1932, John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
published a paper claiming to prove that all hidden variable theories were impossible. (A result found to be flawed by Grete Hermann
Grete Hermann
Grete 'Hermann was a German mathematician and philosopher. She studied mathematics at Göttingen under Emmy Noether, where she achieved her Ph.D. in 1926...
three years later, though this went unnoticed by the physics community for over fifty years). However, in 1952, David Bohm
David Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
, dissatisfied with the prevailing orthodoxy, rediscovered de Broglie's Pilot Wave theory. Bohm developed Pilot Wave Theory into what is now called the De Broglie-Bohm theory.
The de Broglie-Bohm theory itself might have gone unnoticed by most physicists, if it had not been championed by John Bell
John Stewart Bell
John Stewart Bell FRS was a British physicist from Northern Ireland , and the originator of Bell's theorem, a significant theorem in quantum physics regarding hidden variable theories.- Early life and work :...
, who also countered the objections to it. In 1987, John Bell rediscovered Grete Hermann's work, and thus showed the physics community that Pauli's and von Neumann's objections really only showed that the Pilot Wave theory did not have locality; in fact, no quantum-mechanical theories have locality, so these objections did not invalidate the Pilot Wave theory.
The de Broglie-Bohm theory is now considered by some to be a valid challenge to the prevailing orthodoxy of the Copenhagen Interpretation
Copenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
, but it remains controversial.
Yves Couder and co-workers recently discovered a macroscopic pilot wave system in the form of walking droplets. This system exhibits behaviour of a pilot wave, heretofore considered to be reserved to microscopic phenomena.
External links
- "Pilot waves, Bohmian metaphysics, and the foundations of quantum mechanics", lecture course on Pilot wave theory by Mike Towler, Cambridge University (2009).
- "Quantum mechanics writ large", article about walking droplets by John W. M. Bush, Cambridge University (2010).