EP Quantum Mechanics
Encyclopedia
In physics
, EP quantum mechanics is a theory of motion of point particles, partly included in the framework of quantum trajectory representation theories of quantum mechanics, based upon an equivalence postulate similar in content to the equivalence principle
of general relativity
, rather than on the traditional Copenhagen interpretation
of quantum mechanics
. The equivalence postulate states that all one-particle systems can be connected by a non-degenerate coordinate transformation, more precisely by a map over the cotangent bundle
of the position manifold, so that there exists a quantum action function
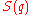transforms as a scalar field
. Here, the action is defined as
is the canonical one-form. This property is the heart of the EP formulation of quantum mechanics. An immediate consequence of the EP is the removal of the rest frame. The theory is based on symmetry properties of Schwarzian derivative
and on the quantum stationary Hamilton-Jacobi equation (QSHJE), which is a partial differential equation
for the quantum action function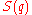
, the quantum version of the Hamilton–Jacobi equation
s differing from the classical one for the presence of a quantum potential term
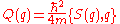
with
denoting the Schwarzian derivative
. The QSHJE can be demonstrated to imply the Schrödinger equation
with square-summability of the wave function, and thus quantization of energy, due to continuity conditions of the quantum potential, without any assumption on the probabilistic interpretation of the wave function. The theory, which is a work in progress, may or may not include probabilistic interpretation as a consequence OR a hidden variable description of trajectories.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, EP quantum mechanics is a theory of motion of point particles, partly included in the framework of quantum trajectory representation theories of quantum mechanics, based upon an equivalence postulate similar in content to the equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, rather than on the traditional Copenhagen interpretation
Copenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The equivalence postulate states that all one-particle systems can be connected by a non-degenerate coordinate transformation, more precisely by a map over the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of the position manifold, so that there exists a quantum action function
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
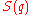transforms as a scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
. Here, the action is defined as
is the canonical one-form. This property is the heart of the EP formulation of quantum mechanics. An immediate consequence of the EP is the removal of the rest frame. The theory is based on symmetry properties of Schwarzian derivative
Schwarzian derivative
In mathematics, the Schwarzian derivative, named after the German mathematician Hermann Schwarz, is a certain operator that is invariant under all linear fractional transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and...
and on the quantum stationary Hamilton-Jacobi equation (QSHJE), which is a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for the quantum action function
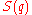, the quantum version of the Hamilton–Jacobi equationHamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s differing from the classical one for the presence of a quantum potential term
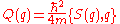
with
denoting the Schwarzian derivativeSchwarzian derivative
In mathematics, the Schwarzian derivative, named after the German mathematician Hermann Schwarz, is a certain operator that is invariant under all linear fractional transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and...
. The QSHJE can be demonstrated to imply the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
with square-summability of the wave function, and thus quantization of energy, due to continuity conditions of the quantum potential, without any assumption on the probabilistic interpretation of the wave function. The theory, which is a work in progress, may or may not include probabilistic interpretation as a consequence OR a hidden variable description of trajectories.