Momentum space
Encyclopedia
The momentum space or k-space associated with a particle
is a vector space
in which every point {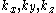
} corresponds to a possible value of the momentum
vector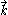
. Representing a problem in terms of the momenta of the particles involved, rather than in terms of their positions, can greatly simplify some problems in physics
.
(weighted sum) of basis states. In principle one is free to choose the set of basis states, as long as they span state space. If one chooses the eigenfunction
s of the position operator
as a set of basis functions, one speaks of a state as a wave function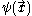
in position space (normal space as we know it). The familiar Schrödinger equation
in terms of the position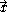
is an example of quantum mechanics in the position representation.
By choosing the eigenfunctions of a different operator as a set of basis functions, one can arrive at a number of different representations of the same state. If one picks the eigenfunctions of the momentum operator as a set of basis functions, the resulting wave function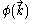
is said to be the wave function in momentum space.
and the concept of frequency domain
. Since a quantum mechanical particle has a frequency proportional to the momentum, describing the particle as a sum of its momentum components is equivalent to describing it as a sum of frequency components (i.e. a Fourier transform). This becomes clear when we ask ourselves how we can transform from one representation to another. Suppose we have a one dimensional wave function in position space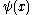
, then we can write this functions as a weighted sum of orthogonal basis functions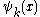 
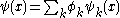
or, in the continuous case, as an integral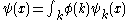
It is clear that if we specify the set of functions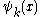
, say as the set of eigenfunctions of the momentum operator, the function 
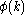holds all the information necessary to reconstruct 
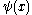and is therefore an alternative description for the state 
.
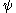In quantum mechanics, the momentum operator
is given by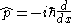
with eigenfunctions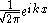
and eigenvalues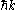
then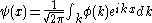
and we see that the momentum representation is related to the position representation by a Fourier transform.
Conversely, in momentum space the position operator is given by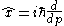
and a similar decomposition can be made of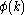
in terms of this operators eigenfunctions.
Particle
A particle is, generally, a small localized object to which can be ascribed physical properties. It may also refer to:In chemistry:* Colloidal particle, part of a one-phase system of two or more components where the particles aren't individually visible.In physics:* Subatomic particle, which may be...
is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
in which every point {
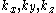} corresponds to a possible value of the momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
vector
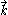. Representing a problem in terms of the momenta of the particles involved, rather than in terms of their positions, can greatly simplify some problems in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
Relation to quantum mechanics
In quantum physics, a particle is described by a quantum state. This quantum state can be represented as a superpositionQuantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
(weighted sum) of basis states. In principle one is free to choose the set of basis states, as long as they span state space. If one chooses the eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s of the position operator
Position operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Consider, for example, the case of a spinless particle moving on a line. The state space for such a particle is L2, the Hilbert space of complex-valued and square-integrable ...
as a set of basis functions, one speaks of a state as a wave function
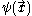in position space (normal space as we know it). The familiar Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
in terms of the position
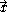is an example of quantum mechanics in the position representation.By choosing the eigenfunctions of a different operator as a set of basis functions, one can arrive at a number of different representations of the same state. If one picks the eigenfunctions of the momentum operator as a set of basis functions, the resulting wave function
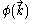is said to be the wave function in momentum space.Relation to frequency domain
The momentum representation of a wave function is very closely related to the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
and the concept of frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
. Since a quantum mechanical particle has a frequency proportional to the momentum, describing the particle as a sum of its momentum components is equivalent to describing it as a sum of frequency components (i.e. a Fourier transform). This becomes clear when we ask ourselves how we can transform from one representation to another. Suppose we have a one dimensional wave function in position space
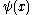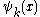
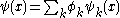
, then we can write this functions as a weighted sum of orthogonal basis functions or, in the continuous case, as an integral
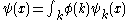
It is clear that if we specify the set of functions
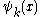, say as the set of eigenfunctions of the momentum operator, the function 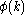holds all the information necessary to reconstruct 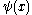and is therefore an alternative description for the state 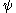.In quantum mechanics, the momentum operator
Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
is given by
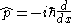
with eigenfunctions
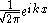
and eigenvalues
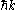
then
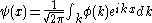
and we see that the momentum representation is related to the position representation by a Fourier transform.
Conversely, in momentum space the position operator is given by
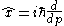
and a similar decomposition can be made of
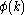in terms of this operators eigenfunctions.