Duffin–Kemmer–Petiau algebra
Encyclopedia
In mathematical physics
, the Duffin–Kemmer–Petiau algebra (DKP algebra), introduced by R.J. Duffin, Nicholas Kemmer
and G. Petiau, is the algebra
which is generated by the Duffin–Kemmer–Petiau matrices. These matrices form part of the Duffin–Kemmer–Petiau equation that provides a relativistic description of spin-0 and spin-1 particles.
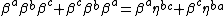
where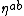
stand for a constant diagonal matrix
. The Duffin–Kemmer–Petiau matrices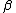
for which 
consists in diagonal elements (+1,-1,…,-1) form part of the Duffin–Kemmer–Petiau equation. Five-dimensional DKP matrices can be represented as:
, 
, 
, 
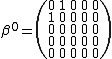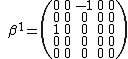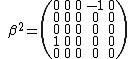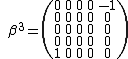
These five-dimensional DKP matrices represent spin-0 particles. The DKP matrices for spin-1 particles are 10-dimensional. The DKP-algebra can be reduced to a direct sum of irreducible subalgebras for spin‐0 and spin‐1 bosons, the subalgebras being defined by multiplication rules for the linearly independent basis elements.
. For particles with nonzero mass, the DKP equation is
where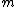
is the particle's mass
,
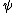its wavefunction
,
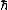the reduced Planck constant
,
the speed of light
. For massless particles, the term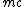
is replaced by a singular matrix 
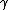that obeys the relations 
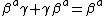and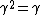 
.
The DKP equation for spin-0 is closely linked to the Klein–Gordon equation. and the equation for spin-1 to the Proca equations
It suffers the same drawback as the Klein–Gordon equation in that it calls for negative probabilities
. Also the De Donder–Weyl covariant Hamiltonian field equations
can be formulated in terms of DKP matrices.
and G. Petiau.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the Duffin–Kemmer–Petiau algebra (DKP algebra), introduced by R.J. Duffin, Nicholas Kemmer
Nicholas Kemmer
Nicholas Kemmer FRS, was a Russian born British nuclear physicist who played an integral and an edge leading role in United Kingdom's nuclear programme, and was known as a mentor of Abdus Salam – a Nobel laureate in Physics....
and G. Petiau, is the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
which is generated by the Duffin–Kemmer–Petiau matrices. These matrices form part of the Duffin–Kemmer–Petiau equation that provides a relativistic description of spin-0 and spin-1 particles.
Defining relations
The Duffin–Kemmer–Petiau matrices have the defining relation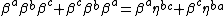where
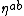stand for a constant diagonal matrixDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. The Duffin–Kemmer–Petiau matrices
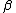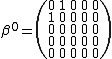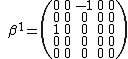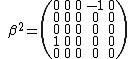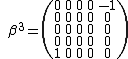
for which consists in diagonal elements (+1,-1,…,-1) form part of the Duffin–Kemmer–Petiau equation. Five-dimensional DKP matrices can be represented as:, , , These five-dimensional DKP matrices represent spin-0 particles. The DKP matrices for spin-1 particles are 10-dimensional. The DKP-algebra can be reduced to a direct sum of irreducible subalgebras for spin‐0 and spin‐1 bosons, the subalgebras being defined by multiplication rules for the linearly independent basis elements.
Duffin–Kemmer–Petiau equation
The Duffin–Kemmer–Petiau equation (DKP equation, also: Kemmer equation) is a relativistic wave equation which describes spin-0 and spin-1 particles in the description of the standard modelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
. For particles with nonzero mass, the DKP equation is
where
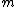is the particle's massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
,
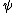its wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
,
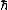the reduced Planck constantPlanck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
,
the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. For massless particles, the term
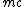is replaced by a singular matrix 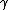that obeys the relations 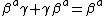and 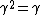.The DKP equation for spin-0 is closely linked to the Klein–Gordon equation. and the equation for spin-1 to the Proca equations
Proca action
In physics, in the area of field theory, the Proca action describes a massive spin-1 field of mass m in Minkowski spacetime. The field involved is a real vector field A...
It suffers the same drawback as the Klein–Gordon equation in that it calls for negative probabilities
Negative probability
In 1942, Paul Dirac wrote a paper "The Physical Interpretation of Quantum Mechanics" where he introduced the concept of negative energies and negative probabilities:...
. Also the De Donder–Weyl covariant Hamiltonian field equations
De Donder–Weyl theory
The De Donder–Weyl theory is a formalism in the calculus of variations over spacetime which treats the space and time coordinates on equal footing. In this framework, a field is represented as a system that varies both in space and in time....
can be formulated in terms of DKP matrices.
History
The Duffin–Kemmer–Petiau algebra was introduced in the 1930s by R.J. Duffin, N. KemmerNicholas Kemmer
Nicholas Kemmer FRS, was a Russian born British nuclear physicist who played an integral and an edge leading role in United Kingdom's nuclear programme, and was known as a mentor of Abdus Salam – a Nobel laureate in Physics....
and G. Petiau.
Further reading
- Pavel Winternitz et al (eds.): Symmetry in physics: in memory of Robert T. Sharp, CRM Proceedings and Lecture Notes, 2004, ISBN 0-8218-3409-6, section “Bhabha and Duffin–Kemmer–Petiau equations: spin zero and spin one”, p. 50 ff.
- V. Ya. Fainberg, B. M. Pimentel: Duffin–Kemmer–Petiau and Klein–Gordon–Fock Equations for Electromagnetic, Yang–Mills and external Gravitational Field Interactions: proof of equivalence, hep-th/0003283, submitted 30. March 2000