
Perron–Frobenius theorem
Encyclopedia
In linear algebra
, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of nonnegative matrices. This theorem has important applications to probability theory (ergodicity of Markov chain
s); to the theory of dynamical systems (subshifts of finite type); to economics (Leontief's input-output model
8.3.6 p. 681);
to demography (Leslie population age distribution model
8.3.7 p. 683);
to mathematical background of the internet search engines
15.2 p. 167 and even to ranking of football
teams p. 80.
"In addition to saying something useful, the Perron–Frobenius theory is elegant. It is a testament to the fact that beautiful mathematics eventually tends to be useful, and useful mathematics eventually tends to be beautiful."
in which all entries are positive real numbers is here called positive and a matrix whose entries are non-negative real numbers is here called non-negative. The eigenvalues of a real square matrix A are complex numbers and collectively they make up the spectrum
of the matrix. The exponential growth rate
of the matrix powers Ak as k → ∞ is controlled by the eigenvalue of A with the largest absolute value
. The Perron–Frobenius theorem describes the properties of the leading eigenvalue and of the corresponding eigenvectors when A is a non-negative real square matrix. Early results were due to and concerned positive matrices. Later, found their extension to certain classes of non-negative matrices.
These claims can be found in Meyer chapter 8 claims 8.2.11-15 page 667 and exercises 8.2.5,7,9 pages 668-669.
The left and right eigenvectors v and w are usually normalized so that the sum of their components is equal to 1; in this case, they are sometimes called stochastic eigenvectors.
In order to highlight the similarities and differences between the two cases
the following points are to be noted: every non-negative matrix can be obviously obtained as a limit of positive matrices, thus
one obtains the existence of an eigenvector with non-negative components; obviously the corresponding eigenvalue will be non-negative and greater or equal in absolute value than all other eigenvalues
(see Meyer chapter 8.3 page 670 or Gantmacher
chapter XIII.3 theorem 3 page 66 for details). However, the simple examples
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of nonnegative matrices. This theorem has important applications to probability theory (ergodicity of Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s); to the theory of dynamical systems (subshifts of finite type); to economics (Leontief's input-output model
Input-output model
In economics, an input-output model is a quantitative economic technique that represents the interdependencies between different branches of national economy or between branches of different, even competing economies. Wassily Leontief developed this type of analysis and took the Nobel Memorial...
8.3.6 p. 681);
to demography (Leslie population age distribution model
Leslie matrix
In applied mathematics, the Leslie matrix is a discrete, age-structured model of population growth that is very popular in population ecology. It was invented by and named after Patrick H. Leslie...
8.3.7 p. 683);
to mathematical background of the internet search engines
PageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
15.2 p. 167 and even to ranking of football
teams p. 80.
"In addition to saying something useful, the Perron–Frobenius theory is elegant. It is a testament to the fact that beautiful mathematics eventually tends to be useful, and useful mathematics eventually tends to be beautiful."
Statement of the Perron–Frobenius theorem
A matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in which all entries are positive real numbers is here called positive and a matrix whose entries are non-negative real numbers is here called non-negative. The eigenvalues of a real square matrix A are complex numbers and collectively they make up the spectrum
Spectrum of a matrix
In mathematics, the spectrum of a matrix is the set of its eigenvalues. This notion can be extended to the spectrum of an operator in the infinite-dimensional case.The determinant equals the product of the eigenvalues...
of the matrix. The exponential growth rate
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
of the matrix powers Ak as k → ∞ is controlled by the eigenvalue of A with the largest absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
. The Perron–Frobenius theorem describes the properties of the leading eigenvalue and of the corresponding eigenvectors when A is a non-negative real square matrix. Early results were due to and concerned positive matrices. Later, found their extension to certain classes of non-negative matrices.
Positive matrices
Let A = (aij) be an n × n positive matrix: aij > 0 for 1 ≤ i, j ≤ n. Then the following statements hold.- There is a positive real number r, called the Perron root or the Perron–Frobenius eigenvalue, such that r is an eigenvalue of A and any other eigenvalue λ (possibly, complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) is strictly smaller than r in absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
, |λ| < r. Thus, the spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
ρ(A) is equal to r. - The Perron–Frobenius eigenvalue is simple: r is a simple root of the characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of A. Consequently, the eigenspace associated to r is one-dimensional. (The same is true for the left eigenspace, i.e., the eigenspace for AT.) - There exists an eigenvector v = (v1,…,vn) of A with eigenvalue r such that all components of v are positive: A v = r v, vi > 0 for 1 ≤ i ≤ n. (Respectively, there exists a positive left eigenvector w : wT A = r wT, wi > 0.)
- There are no other positive (moreover non-negative) eigenvectors except positive multiples of v (respectively, left eigenvectors except w), i.e. all other eigenvectors must have at least one negative or non-real component.
-
 , where the left and right eigenvectors for A are normalized so that wTv = 1. Moreover, the matrix v wT is the projection onto the eigenspace corresponding to r. This projection is called the Perron projection.
, where the left and right eigenvectors for A are normalized so that wTv = 1. Moreover, the matrix v wT is the projection onto the eigenspace corresponding to r. This projection is called the Perron projection. - CollatzLothar CollatzLothar Collatz was a German mathematician. In 1937 he posed the famous Collatz conjecture, which remains unsolved....
–Wielandt formula: for all non-negative non-zero vectors x, let f(x) be the minimum value of [Ax]i / xi taken over all those i such that xi ≠ 0. Then f is a real valued function whose maximum is the Perron–Frobenius eigenvalue. - A "Min-max" Collatz–Wielandt formula takes a form similar to the one above: for all strictly positive vectors x, let g(x) be the maximum value of [Ax]i / xi taken over i. Then g is a real valued function whose minimum is the Perron–Frobenius eigenvalue.
- The Perron–Frobenius eigenvalue satisfies the inequalities
These claims can be found in Meyer chapter 8 claims 8.2.11-15 page 667 and exercises 8.2.5,7,9 pages 668-669.
The left and right eigenvectors v and w are usually normalized so that the sum of their components is equal to 1; in this case, they are sometimes called stochastic eigenvectors.
Non-negative matrices
An extension of the theorem to matrices with non-negative entries is also available.In order to highlight the similarities and differences between the two cases
the following points are to be noted: every non-negative matrix can be obviously obtained as a limit of positive matrices, thus
one obtains the existence of an eigenvector with non-negative components; obviously the corresponding eigenvalue will be non-negative and greater or equal in absolute value than all other eigenvalues
(see Meyer chapter 8.3 page 670 or Gantmacher
Felix Gantmacher
Felix Gantmacher was a Soviet mathematician, professor at Moscow Institute of Physics and Technology, well-known for his contributions in mechanics, matrix theory and Lie group theory....
chapter XIII.3 theorem 3 page 66 for details). However, the simple examples
-

show that for non-negative matrices there may exist eigenvalues of the same absolute value as the maximal one ((1) and (−1) – eigenvalues of the first matrix); moreover the maximal eigenvalue may not be a simple root of the characteristic polynomial, can be zero and the corresponding eigenvector (1,0) is not strictly positive (second example). So it may seem that most properties are broken for non-negative matrices, however Frobenius found the right way.
The key feature of theory in the non-negative case is to find some special subclass of non-negative matrices – irreducible matrices – for which a non-trivial generalization is possible. Namely, although eigenvalues attaining maximal absolute value may not be unique, the structure of maximal eigenvalues is under control: they have the form ei2πl/hr, where h is some integer number – periodIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of matrix, r is a real strictly positive eigenvalue, l = 0, 1, ..., h − 1.
The eigenvector corresponding to r has strictly positive components (in contrast with the general case of non-negative matrices, where components are only non-negative).
Also all such eigenvalues are simple roots of the characteristic polynomial. Further properties are described below.
Classification of matrices
Let A be a square matrix (not necessarily positive or even real).
The matrix A is irreducible if any of the following equivalent properties
holds.
Definition 1 : A does not have non-trivial invariant coordinate subspaces.
Here a non-trivial coordinate subspace means a linear subspaceLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
spanned by any proper subset of basis vectors. More explicitly, for any linear subspace spanned by basis vectors ei1 , ...,
eik, n > k > 0 its image under the action of A is not contained in the same subspace.
Definition 2: A cannot be conjugated into block upper triangular form by a permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
P:-
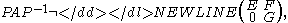
where E and G are non-trivial (i.e. of size greater than zero) square matrices.
If A is non-negative other definitions exist:
Definition 3: For every pair of indices i and j, there exists a natural number m such that (Am)ij is not equal to 0.
Definition 4: One can associate with a matrix A a certain directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
GA. It has exactly n vertices, where n is size of A, and there is an edge from vertex i to vertex j precisely when Aij > 0. Then the matrix A is irreducible if and only if its associated graph GA is strongly connectedStrongly connected componentA directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
.
A matrix is reducible if it is not irreducible.
Let A be non-negative.
Fix an index i and define the period of index i to be the greatest common divisorGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of all natural numbers m such that (Am)ii > 0. When A is irreducible, the period of every index is the same and is called the period of A.
When A is also irreducible, the period can be defined as the greatest common divisor of the lengths of the closed directed paths in GA (see Kitchens page 16). The period is also called the index of imprimitivity
(Meyer page 674) or the order of cyclicity.
If the period is 1, A is aperiodic.
A matrix A is primitive if it is non-negative and its mth power is positive for some natural number m (i.e. the same m works for all pairs of indices).
It can be proved that primitive matrices are the same as irreducible aperiodic non-negative matrices.
A positive square matrix is primitive and a primitive matrix is irreducible. All statements of the Perron–Frobenius theorem for positive matrices remain true for primitive matrices. However, a general non-negative irreducible matrix A may possess several eigenvalues whose absolute value is equal to the spectral radius of A, so the statements need to be correspondingly modified. Actually the number of such eigenvalues is exactly equal to the period. Results for non-negative matrices were first obtained by Frobenius in 1912.
Perron–Frobenius theorem for irreducible matrices
Let A be an irreducible non-negative n × n matrix with period h and spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
ρ(A) = r. Then the following statements hold.
- The number r is a positive real number and it is an eigenvalue of the matrix A, called the Perron–Frobenius eigenvalue.
- The Perron–Frobenius eigenvalue r is simple. Both right and left eigenspaces associated with r are one-dimensional.
- A has a left eigenvector v with eigenvalue r whose components are all positive.
- Likewise, A has a right eigenvector w with eigenvalue r whose components are all positive.
- The only eigenvectors whose components are all positive are those associated with the eigenvalue r.
- Matrix A has exactly h (where h is the period) complex eigenvalues with absolute value r. Each of them is a simple root of the characteristic polynomial and is the product of r with an hth root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
. - Let ω = 2π/h. Then the matrix A is similar to eiωA, consequently the spectrum of A is invariant under multiplication by eiω (corresponding to the rotation of the complex plane by the angle ω).
- If h > 1 then there exists a permutation matrix P such that
-
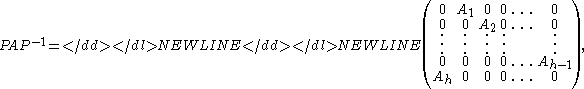
-
- where the blocks along the main diagonal are zero square matrices.
- 9. CollatzLothar CollatzLothar Collatz was a German mathematician. In 1937 he posed the famous Collatz conjecture, which remains unsolved....
–Wielandt formula: for all non-negative non-zero vectors x let f(x) be the minimum value of [Ax]i / xi taken over all those i such that xi ≠ 0. Then f is a real valued function whose maximum is the Perron–Frobenius eigenvalue.
- 10. The Perron–Frobenius eigenvalue satisfies the inequalities
The matrix shows that the blocks on the diagonal may be of different sizes, the matrices Aj need not be square, and h need not divide n.
shows that the blocks on the diagonal may be of different sizes, the matrices Aj need not be square, and h need not divide n.
Further properties
Let A be an irreducible non-negative matrix, then:- (1+A)n−1 is a positive matrix. (Meyer claim 8.3.5 p. 672).
- Wielandt's theorem. If |B|<A, then ρ(B)≤ρ(A). If equality holds (i.e. if μ=ρ(A)eiφ is eigenvalue for B), then B = eiφ D AD−1 for some diagonal unitary matrix D (i.e. diagonal elements of D equals to eiΘl, non-diagonal are zero). (Meyer claim 8.3.11 p. 675).
- If some power Aq is reducible, then it is completely reducible, i.e. for some permutation matrix P, it is true that:
 , where Ai are irreducible matrices having the same maximal eigenvalue. The number of these matrices d is the greatest common divisor of q and h, where h is period of A. (GantmacherFelix GantmacherFelix Gantmacher was a Soviet mathematician, professor at Moscow Institute of Physics and Technology, well-known for his contributions in mechanics, matrix theory and Lie group theory....
, where Ai are irreducible matrices having the same maximal eigenvalue. The number of these matrices d is the greatest common divisor of q and h, where h is period of A. (GantmacherFelix GantmacherFelix Gantmacher was a Soviet mathematician, professor at Moscow Institute of Physics and Technology, well-known for his contributions in mechanics, matrix theory and Lie group theory....
section XIII.5 theorem 9).- If c(x)=xn+ck1 xn-k1 +ck2 xn-k2 + ... + cks xn-ks is the characteristic polynomial of A in which the only nonzero coefficients are listed, then the period of A equals to the greatest common divisor for k1, k2, ... , ks.(Meyer page 679).
- CesàroCesàro summationIn mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
averages: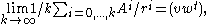 where the left and right eigenvectors for A are normalized so that wtv = 1. Moreover the matrix v wt is the spectral projection corresponding to r - Perron projection. (Meyer example 8.3.2 p. 677).
where the left and right eigenvectors for A are normalized so that wtv = 1. Moreover the matrix v wt is the spectral projection corresponding to r - Perron projection. (Meyer example 8.3.2 p. 677). - Let r be the Perron-Frobenius eigenvalue, then the adjoint matrix for (r-A) is positive (GantmacherFelix GantmacherFelix Gantmacher was a Soviet mathematician, professor at Moscow Institute of Physics and Technology, well-known for his contributions in mechanics, matrix theory and Lie group theory....
section XIII.2.2 page 62). - If A has at least one non-zero diagonal element, then A is primitive. (Meyer example 8.3.3 p. 678).
The following facts worth to be mentioned.- If 0 ≤ A < B, the rA ≤ rB, moreover, if A is irreducible, then the inequality is strict: rA < rB.
One of the definitions of primitive matrix requires A to be non-negative and there exists m, such that Am is positive. One may one wonder how big m can be, depending on the size of A. The following answers this question.- Assume A is non-negative primitive matrix of size n, then An2-2n+2 is positive. Moreover there exists a matrix M given below, such that Mk remains not positive (just non-negative) for all k< n2-2n+2, in particular (Mn2-2n+1)11=0.

(Meyer chapter 8 example 8.3.4 page 679 and exercise 8.3.9 p. 685).
Applications
Numerous books have been written on the subject of non-negative matrices, and Perron–Frobenius theory is invariably a central feature. So there is a vast application area and the examples given below barely begin to scratch its surface.
Non-negative matrices
The Perron–Frobenius theorem does not apply directly to non-negative matrices. Nevertheless any reducible square matrix A may be written in upper-triangular block form (known as the normal form of a reducible matrix)-
-
-
- PAP−1 =
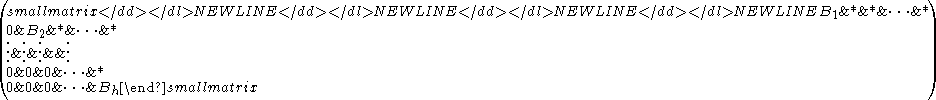
where P is a permutation matrix and each Bi is a square matrix that is either irreducible or zero. Now if A is non-negative then so are all the Bi and the spectrum of A is just the union of their spectra. Therefore many of the spectral properties of A may be deduced by applying the theorem to the irreducible Bi.
For example the Perron root is the maximum of the ρ(Bi). Whilst there will still be eigenvectors with non-negative components it is quite possible that none of these will be positive.
Stochastic matrices
A row (column) stochastic matrixStochastic matrixIn mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
is a square matrix each of whose rows (columns) consists of non-negative real numbers whose sum is unity. The theorem cannot be applied directly to such matrices because they need not be irreducible.
If A is row-stochastic then the column vector with each entry 1 is an eigenvector corresponding to the eigenvalue 1, which is also ρ(A) by the remark above. It may not be the only eigenvalue on the unit circle: and the associated eigenspace can be multi-dimensional. If A is row-stochastic and irreducible then the Perron projection is also row-stochastic and all its rows are equal.
Algebraic graph theory
The theorem has particular use in algebraic graph theoryAlgebraic graph theoryAlgebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...
. The "underlying graph" of a nonnegative n-square matrix is the graph with vertices numbered 1, ..., n and arc ij if and only if Aij ≠ 0. If the underlying graph of such a matrix is strongly connected, then the matrix is irreducible, and thus the theorem applies. In particular, the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of a
strongly connected graphStrongly connected componentA directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
is irreducible.
Finite Markov chains
The theorem has a natural interpretation in the theory of finite Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s (where it is the matrix-theoretic equivalent of the convergence of an irreducible finite Markov chain to its stationary distribution, formulated in terms of the transition matrix of the chain; see, for example, the article on the subshift of finite typeSubshift of finite typeIn mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
).
Compact operators
More generally, it can be extended to the case of non-negative compact operatorCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s, which, in many ways, resemble finite-dimensional matrices. These are commonly studied in physics, under the name of transfer operatorTransfer operatorIn mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
s, or sometimes Ruelle–Perron–Frobenius operators (after David RuelleDavid RuelleDavid Pierre Ruelle is a Belgian-French mathematical physicist. He has worked on statistical physics and dynamical systems. With Floris Takens he coined the term strange attractor, and founded a new theory of turbulence...
). In this case, the leading eigenvalue corresponds to the thermodynamic equilibriumThermodynamic equilibriumIn thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
of a dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, and the lesser eigenvalues to the decay modes of a system that is not in equilibrium. Thus, the theory offers a way of discovering the arrow of timeArrow of timeThe arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
in what would otherwise appear to be reversible, deterministic dynamical processes, when examined from the point of view of point-set topology.
Proof methods
A common thread in many proofs is the Brouwer fixed point theoremBrouwer fixed point theoremBrouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
. Another popular method is that of Wielandt (1950). He used the CollatzLothar CollatzLothar Collatz was a German mathematician. In 1937 he posed the famous Collatz conjecture, which remains unsolved....
–Wielandt formula described above to extend and clarify Frobenius's work
(see GantmacherFelix GantmacherFelix Gantmacher was a Soviet mathematician, professor at Moscow Institute of Physics and Technology, well-known for his contributions in mechanics, matrix theory and Lie group theory....
section XIII.2.2
page 54
).
The proof based on the spectral theorySpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
can be found in from which part of the arguments are borrowed.
Perron root is strictly maximal eigenvalue for positive (and primitive) matrices
- If A is a positive (or more generally primitive) matrix, then there exists real positive eigenvalue r (Perron-Frobenius eigenvalue or Perron root), which is strictly greater in absolute value than all other eigenvalues, hence r is the spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of A.
Pay attention that claim is wrong for general non-negative irreducible matrices, which have h eigenvalues with the same absolute eigenvalue as r, where h is the period of A.
Proof. Consider first the case of positive matrices.
Let A be a positive matrix, assume that its spectral radius ρ(A) = 1 (otherwise consider A/ρ(A)). Hence, as it is known, there exists an eigenvalue λ on the unit circle, and all the other eigenvalues are less or equal 1 in absolute value. Assume that that λ ≠ 1. Then there exists a positive integer m such that Am is a positive matrix and the real part of λm is negative. Let ε be half the smallest diagonal entry of Am and set T = Am − ε1 which is yet another positive matrix. Moreover if Ax = λx then Amx = λmx thus λm − ε is an eigenvalue of T. Because of the choice of m this point lies outside the unit disk consequently ρ(T) > 1. On the other hand all the entries in T are positive and less than or equal to those in Am so by Gelfand's formulaSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
ρ(T) ≤ ρ(Am) ≤ ρ(A)m = 1. This contradiction means that λ=1 and there can be no other eigenvalues on the unit circle.
Proof for positive matrices is finished .
Absolutely the same arguments can be applied to the case of primitive matrices, after one just need to mention the following simple lemma, which clarifies the properties of primitive matrices
Lemma: Consider a non-negative A. Assume there exists m, such that Am is positive, then Am+1, Am+2, Am+3,... are all positive.
Indeed, Am+1= A Am, so it can have zero element only if some row of A is entirely zero, but in this case the same row of Am will be zero. Lemma is proved.
After lemma is established one applies the same arguments as above for primitive matrices to prove the main claim.
Power method and the positive eigenpair
- for a positive (or more generally irreducible non-negative) matrix A the dominant eigenvector is real and strictly positive (for non-negative A respectively non-negative)
It can be argued by the power method, which states that for sufficiently generic (in the sense discussed below) matrix A the sequence of vectors bk+1=Abk / | Abk | converges to the eigenvector with the maximum eigenvalue. (Initial vector b0 can be chosen arbitrary except some measure zero set). Starting with a non-negative vector b0 one gets the sequence of non-negative vectors bk. Hence the limiting vector is also non-negative. By power method this limiting vector is the desired the dominant eigenvector for A, so assertion is proved. Corresponding eigenvalue is clearly non-negative.
To accomplish the proof two arguments should be added. First,
the power method converges for matrices which does not have several eigenvalues of the same absolute value as the maximal one. The previous section argument guarantees this.
Second, is to ensure strict positivity of all of the components of the eigenvector for the case of irreducible matrices.
This follows from the following simple fact, which is of independent interest:
- Lemma: consider a positive (or more generally irreducible non-negative) matrix A. Assume v is any non-negative eigenvector for A, then it is necessarily strictly positive and corresponding eigenvalue is also strictly positive.
Proof. Recall that one of the definitions of irreducibility for non-negative matrices is that for all indexes i,j there exists m, such that (Am)ij is strictly positive. Consider a non-negative eigenvector v, assume that at least one of its components say j-th is strictly positive. Then one can deduce that the corresponding eigenvalue is strictly positive, indeed, consider n such that (An)ii >0, hence: rnvi =
Anvi >=
(An)iivi
>0. Hence r is strictly positive. In the same manner one can deduce strict positivity of the eigenvector. To prove it, consider m, such that (Am)ij >0, hence: rmvj =
(Amv)j >=
(Am)ijvi >0, hence
vj is strictly positive, i.e. eigenvector is strictly positive.
Proof is finished.
Multiplicity one
The proof that the Perron-Frobenius eigenvalue is simple root of the characteristic polynomial is also elementary. The arguments here are close to that ones in Meyer chapter 8 page 665, where details can be found.
- Eigenspace associated to Perron-Frobenius eigenvalue r is one-dimensional
Consider strictly positive eigenvector v corresponding to r.
Assume there exists another eigenvector w with the same eigenvalue. (Vector w can be chosen to be real, because A and r are both real, so the null space of A-r has a basis consisting of real vectors). Assume at least one of the components of w is positive (otherwise multiply w by -1).
Consider maximal possible α such that u=v- α w is non-negative.
Then clearly one of the components of u is zero, otherwise α is not maximum. Obviously vector u is an eigenvector. It is non-negative, hence by the lemma described in the
previous section non-negativity implies strict positivity for any eigenvector.
On the other hand it was stated just above that at least one component of u is zero. The contradiction implies, that w does not exist. The claim is proved.
- There is no Jordan cells corresponding to the Perron-Frobenius eigenvalue r and all other eigenvalues which has the same absolute value
The idea is the following: if there is a Jordan cell, then the infinity norm
||(A/r)k||∞ tends to infinity for k → ∞ ,
but it will actually contradict the existence of the positive eigenvector.
The details are the following. Assume r=1, otherwise consider A/r. Let v be Perron-Frobenius strictly positive eigenvector, so Av=v, then:
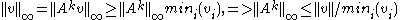
So ||Ak||∞ is bounded for all k.
Actually it gives another proof that there is no eigenvalues which has greater absolute value then Perron-Frobenius one. And it gives more. It contradicts the existence of the Jordan cell for any eigenvalue which has absolute value equal to 1 (in particular for the Perron-Frobenius one), because existence of the Jordan cell implies that ||Ak||∞ is unbounded. For example for two by two matrix:-

hence ||Jk||∞ = |k+λ| (for |λ|=1), so it tends to infinity when k does so.
Since ||Jk|| = ||C-1 AkC ||,
then || Ak || >= ||Jk||/ ( ||C−1|| || C ||), so it also tends to infinity.
Obtained contradiction implies that there is no Jordan cells for the corresponding eigenvalues. Proof is finished.
Combining the two claims above together one gets:- the Perron-Frobenius eigenvalue r is simple root of the characteristic polynomial.
Actually in the case of non primitive matrices, there exists other eigenvalues which has the same absolute value as r.
Same claim is true for them, but it requires more work.
No other non-negative eigenvectors
- Consider positive (or more generally irreducible non-negative matrix) A. The Perron-Frobenius eigenvector is the only (up to multiplication by constant) non-negative eigenvector for A.
So other eigenvectors should contain negative, or complex components.
The idea of proof is the following - eigenvectors for different eigenvalues should be orthogonal in some sense, however two positive eigenvectors cannot be orthogonal, so they correspond the same eigenvalue, but eigenspace for the Perron-Frobenius is one dimensional.
The formal proof goes as follows.
Assume there exists an eigenpair (λ, y) for A, such that vector y is positive.
Consider (r, x), where x - is the right Perron-Frobenius eigenvector for A (i.e. eigenvector for At). Then:
r xt y = (xt A) y= xt (A y)=λ xt y, also xt y >0, so one has: r=λ.
But eigenspace for the Perron-Frobenius eigenvalue r is one dimensional, as it was established before. Hence non-negative eigenvector y is multiple of the Perron-Frobenius one. Assertion is proved.
One can consult Meyer chapter 8 claim 8.2.10 page 666 for details.
Collatz–Wielandt formula
- Consider positive (or more generally irreducible non-negative matrix) A. For all non-negative non-zero vectors x let f(x) be the minimum value of [Ax]i / xi taken over all those i such that xi ≠ 0. Then f is a real valued function whose maximum is the Perron–Frobenius eigenvalue r.
First observe that r is attained for x taken to be the Perron-Frobenius eigenvector v. So one needs to prove that values f on the other vectors are less or equal. Consider some vector x. Let ξ=f(x), so 0<= ξx <=Ax. Consider w to be the right eigenvector for A. Hence wt ξx <= wt (Ax) = (wt A)x = r wt x . Hence ξ<=r. So proof is finished.
One can consult Meyer chapter 8 page 666 for details.
Perron projection as a limit: Ak/rk
Consider positive (or more generally primitive) matrix A, and r its Perron-Frobenius eigenvalue, then:-
- There exists a limit Ak/rk for k → ∞, denote it by P.
- P is a projection operatorProjection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
: P2=P, which commutes with A: AP=PA. - The image of P is one-dimensional and spanned by the Perron-Frobenius eigenvector v (respectively for Pt - by the Perron-Frobenius eigenvector w for At).
- P= v wt, where v,w are normalized such that w^t v = 1.
- Hence P is a positive operator.
Hence P is a spectral projection for the Perron-Frobenius eigenvalue r, and it is called Perron projection.
Pay attention: the assertion above is not true for general non-negative irreducible matrices.
Actually the claims above (except claim 5) are valid for any matrix M such that there exists an eigenvalue r, which is strictly greater than the other eigenvalues in absolute value and it is simple root of the characteristic polynomial. (These requirements hold for primitive matrices as it was shown above). The proof of this more general fact is sketched below.
Proof.
One can demonstrate the existence of the limit as follows.
Assume M is diagonalizable, so it is conjugate to diagonal matrix with eigenvalues r1, ... , rn on the diagonal
(denote r1=r). The matrix Mk/rk will be conjugate (1, (r2/r)k, ... , (rn/r)k), which tends to (1,0,0,...,0), for k → ∞. So the limit exists. The same method works for general M (without assumption M is diagonalizable).
The projection and commutativity properties are elementary corollaries of the definition: M Mk/rk= Mk/rk M ; P2 = lim M2k/r2k=P.
The third fact is also elementary: M (P u)= M lim Mk/rk u = lim r Mk+1/rk+1 u, so taking the limit one gets M (P u)=r (P u), so image of P lies in the r-eigenspace for M, which is one-dimensional by the assumptions.
Denote by v r-eigenvector for M (by w for Mt).
Columns of P are multiples of v, because image of P is spanned by it. Respectively rows - of w.
So P takes a form (a v wt), for some a.
Hence its trace equals to (a wt v). On the other hand trace of projector equals to the dimension of its image.
It was proved before that it is not more than one-dimensional.
From the definition one sees that P acts identically on the r-eigenvector for M. So it is one-dimensional.
So one concludes that choosing (wt v)=1, implies P=v wt.
The proof is finished.
Inequalities for Perron–Frobenius eigenvalue
For any non-nonegative matrix A its Perron–Frobenius eigenvalue r
satisfies the inequality:
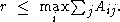
Actually it is not specific to non-negative matrices: for any matrix A and any its eigenvalue λ it is true
that . This is immediate corollary of the
. This is immediate corollary of the
Gershgorin circle theoremGershgorin circle theoremIn mathematics, the Gershgorin circle theorem may be used to bound the spectrum of a square matrix. It was first published by the Belarusian mathematician Semyon Aranovich Gershgorin in 1931. The spelling of S. A...
. However there is another proof which is more direct.
Any matrix induced norm satisfies the inequality ||A|| ≥ |λ| for any eigenvalue λ, because ||A|| ≥ ||Ax||/||x|| = ||λx||/||x|| = |λ|. The infinity norm of a matrix is the maximum of row sums: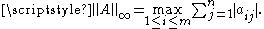 Hence the desired inequality is exactly ||A||∞ ≥ |λ| applied to non-negative matrix A.
Hence the desired inequality is exactly ||A||∞ ≥ |λ| applied to non-negative matrix A.
Another inequality is:

This fact is specific for non-negative matrices, for general matrices there is nothing similar. To prove it one first
suppose that A is positive (non just non-negative). Then there exists a positive eigenvector w such that Aw = rw and the smallest component of w (say wi) is 1. Then r = (Aw)i ≥ the sum of the numbers in row i of A. Thus the minimum row sum gives a lower bound for r and this observation can be extended to all non-negative matrices by continuity.
Another way to argue it is via the CollatzLothar CollatzLothar Collatz was a German mathematician. In 1937 he posed the famous Collatz conjecture, which remains unsolved....
-Wielandt formula. One takes the vector x = (1, 1, ..., 1) and immediately obtains the inequality.
Perron projection
The proof now proceeds using spectral decomposition. The trick here is to split the Perron root away from the other eigenvalues. The spectral projection associated with the Perron root is called the Perron projection and it enjoys the following property:- The Perron projection of an irreducible non-negative square matrix is a positive matrix.
Perron's findings and also (1)–(5) of the theorem are corollaries of this result. The key point is that a positive projection always has rank one. This means that if A is an irreducible non-negative square matrix then the algebraic and geometric multiplicities of its Perron root are both one. Also if P is its Perron projection then AP = PA = ρ(A)P so every column of P is a positive right eigenvector of A and every row is a positive left eigenvector. Moreover if Ax = λx then PAx = λPx = ρ(A)Px which means Px = 0 if λ ≠ ρ(A). Thus the only positive eigenvectors are those associated with ρ(A). And there is yet more to come. If A is a primitive matrix with ρ(A) = 1 then it can be decomposed as P ⊕ (1 − P)A so that An = P + (1 − P)An. As n increases the second of these terms decays to zero leaving P as the limit of An as n → ∞.
The power method is a convenient way to compute the Perron projection of a primitive matrix. If v and w are the positive row and column vectors that it generates then the Perron projection is just wv/vw. It should be noted that the spectral projections aren't neatly blocked as in the Jordan form. Here they are overlaid on top of one another and each generally has complex entries extending to all four corners of the square matrix. Nevertheless they retain their mutual orthogonality which is what facilitates the decomposition.
Peripheral projection
The analysis when A is irreducible and non-negative is broadly similar. The Perron projection is still positive but there may now be other eigenvalues of modulus ρ(A) that negate use of the power method and prevent the powers of (1 − P)A decaying as in the primitive case whenever ρ(A) = 1. So enter the peripheral projection which is the spectral projection of A corresponding to all the eigenvalues that have modulus ρ(A) ....- The peripheral projection of an irreducible non-negative square matrix is a non-negative matrix with a positive diagonal.
Cyclicity
Suppose in addition that ρ(A) = 1 and A has h eigenvalues on the unit circle. If P is the peripheral projection then the matrix R = AP = PA is non-negative and irreducible, Rh = P, and the cyclic group P, R, R2, ...., Rh−1 represents the harmonics of A. The spectral projection of A at the eigenvalue λ on the unit circle is given by the formula . All of these projections (including the Perron projection) have the same positive diagonal, moreover choosing any one of them and then taking the modulus of every entry invariably yields the Perron projection. Some donkey work is still needed in order to establish the cyclic properties (6)–(8) but it's essentially just a matter of turning the handle. The spectral decomposition of A is given by A = R ⊕ (1 − P)A so the difference between An and Rn is An − Rn = (1 − P)An representing the transients of An which eventually decay to zero. P may be computed as the limit of Anh as n → ∞.
. All of these projections (including the Perron projection) have the same positive diagonal, moreover choosing any one of them and then taking the modulus of every entry invariably yields the Perron projection. Some donkey work is still needed in order to establish the cyclic properties (6)–(8) but it's essentially just a matter of turning the handle. The spectral decomposition of A is given by A = R ⊕ (1 − P)A so the difference between An and Rn is An − Rn = (1 − P)An representing the transients of An which eventually decay to zero. P may be computed as the limit of Anh as n → ∞.
Caveats
The matrices L =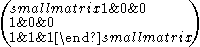 , P =
, P = 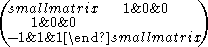 , T =
, T = 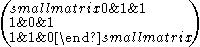 , M =
, M =  provide simple examples of what can go wrong if the necessary conditions are not met. It is easily seen that the Perron and peripheral projections of L are both equal to P, thus when the original matrix is reducible the projections may lose non-negativity and there is no chance of expressing them as limits of its powers. The matrix T is an example of a primitive matrix with zero diagonal. If the diagonal of an irreducible non-negative square matrix is non-zero then the matrix must be primitive but this example demonstrates that the converse is false. M is an example of a matrix with several missing spectral teeth. If ω = eiπ/3 then ω6 = 1 and the eigenvalues of M are {1,ω2,ω3,ω4} so ω and ω5 are both absent.
provide simple examples of what can go wrong if the necessary conditions are not met. It is easily seen that the Perron and peripheral projections of L are both equal to P, thus when the original matrix is reducible the projections may lose non-negativity and there is no chance of expressing them as limits of its powers. The matrix T is an example of a primitive matrix with zero diagonal. If the diagonal of an irreducible non-negative square matrix is non-zero then the matrix must be primitive but this example demonstrates that the converse is false. M is an example of a matrix with several missing spectral teeth. If ω = eiπ/3 then ω6 = 1 and the eigenvalues of M are {1,ω2,ω3,ω4} so ω and ω5 are both absent.
Terminology
A problem that causes confusion is a lack of standardisation in the definitions. For example, some authors use the terms strictly positive and positive to mean > 0 and ≥ 0 respectively. In this article positive means > 0 and non-negative means ≥ 0. Another vexed area concerns decomposability and reducibility: irreducible is an overloaded term. For avoidance of doubt a non-zero non-negative square matrix A such that 1 + A is primitive is sometimes said to be connected. Then irreducible non-negative square matrices and connected matrices are synonymous.
The nonnegative eigenvector is often normalized so that the sum of its components is equal to unity; in this case, the eigenvector is a the vector of a probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
and is sometimes called a stochastic eigenvector.
Perron–Frobenius eigenvalue and dominant eigenvalue are alternative names for the Perron root. Spectral projections are also known as spectral projectors and spectral idempotents. The period is sometimes referred to as the index of imprimitivity or the order of cyclicity.
See also
- Z-matrix (mathematics)
- M-matrixM-matrixIn mathematics, especially linear algebra, an M-matrix is a Z-matrix with eigenvalues whose real parts are positive. M-matrices are a subset of the class of P-matrices, and also of the class of inverse-positive matrices In mathematics, especially linear algebra, an M-matrix is a Z-matrix with...
- P-matrix
- L-matrix
- Hurwitz matrixHurwitz matrix-Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...
- Metzler matrix (Quasipositive matrixQuasipositive matrixIn mathematics, a Metzler matrix is a matrix in which all the off-diagonal components are nonnegative It is named after the American economist Lloyd Metzler....
) - Positive operator
Further reading
- Abraham Berman, Robert J. Plemmons, Nonnegative Matrices in the Mathematical Sciences, 1994, SIAM. ISBN 0-89871-321-8.
- Chris GodsilChris GodsilChristopher David Godsil is a professor at the Department of Combinatorics and Optimization in the faculty of mathematics at the University of Waterloo. He wrote the popular textbook on algebraic graph theory, entitled Algebraic graph theory, with Gordon Royle, His earlier textbook on...
and Gordon RoyleGordon RoyleGordon F. Royle is a Professor at the School of Mathematics and Statistics at The University of Western Australia. He is well known for his research into the mathematics of Sudoku and his search for the Sudoku puzzle with the smallest number of entries that has a unique solution.-See...
, Algebraic Graph Theory, Springer, 2001. - A. Graham, Nonnegative Matrices and Applicable Topics in Linear Algebra, John Wiley&Sons, New York, 1987.
- R. A. Horn and C.R. Johnson, Matrix Analysis, Cambridge University Press, 1990
- S. P. Meyn and R. L. Tweedie, Markov Chains and Stochastic Stability London: Springer-Verlag, 1993. ISBN 0-387-19832-6 (2nd edition, Cambridge University Press, 2009)
- Henryk Minc, Nonnegative matrices, John Wiley&Sons, New York, 1988, ISBN 0-471-83966-3
- Seneta, E. Non-negative matrices and Markov chains. 2nd rev. ed., 1981, XVI, 288 p., Softcover Springer Series in Statistics. (Originally published by Allen & Unwin Ltd., London, 1973) ISBN 978-0-387-29765-1 (The claim that Aj has order n/h at the end of the statement of the theorem is incorrect.)
- Richard S. VargaRichard S. VargaRichard Steven Varga is an American mathematician who specializes in numerical analysis and linear algebra. He is currently a University Professor of Mathematical Sciences at Kent State University, Kent, Ohio...
, Matrix Iterative Analysis, 2nd ed., Springer-Verlag, 2002
- If A is a positive (or more generally primitive) matrix, then there exists real positive eigenvalue r (Perron-Frobenius eigenvalue or Perron root), which is strictly greater in absolute value than all other eigenvalues, hence r is the spectral radius
- PAP−1 =
-
-
-
-
-



