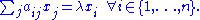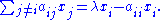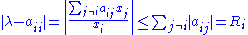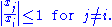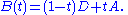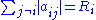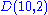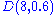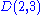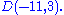Gershgorin circle theorem
Encyclopedia
In mathematics
, the Gershgorin circle theorem may be used to bound the spectrum of a square matrix
. It was first published by the Belarusian mathematician Semyon Aranovich Gershgorin
in 1931. The spelling of S. A. Gershgorin's name has been transliterated in several different ways, including Geršgorin, Gerschgorin, Gershgorin and Hershhorn/Hirschhorn, the latter corresponding to the transliteration of the Yiddish spelling of his name, which is .
n × n matrix, with entries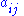
. For i ∈ {1, …, n} let 
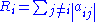be the sum of the absolute value
s of the non-diagonal entries in the ith row. Let D(aii, Ri) be the closed disc centered at aii with radius Ri. Such a disc is called a Gershgorin disc.
Theorem: Every eigenvalue of A lies within at least one of the Gershgorin discs D(aii, Ri).
Proof: Let λ be an eigenvalue of A and let x = (xj) be a corresponding eigenvector. Let i ∈ {1, …, n} be chosen so that |xi| = maxj |xj|. (That is to say, choose i so that xi is the largest (in absolute value) number in the vector x) Then |xi| > 0, otherwise x = 0. Since x is an eigenvector, Ax = λx, and thus:
So, splitting the sum, we get
We may then divide both sides by xi (choosing i as we explained we can be sure that xi ≠ 0) and take the absolute value to obtain
where the last inequality is valid because
Corollary: The eigenvalues of A must also lie within the Gershgorin discs Cj corresponding to the columns of A.
Proof: Apply the Theorem to AT.
Example For a diagonal matrix
, the Gershgorin discs coincide with the spectrum. Conversely, if the Gershgorin discs coincide with the spectrum, the matrix is diagonal.
Theorem: If the union of k discs is disjoint from the union of the other n − k discs then the former union contains exactly k and the latter n − k eigenvalues of A.
Proof: Let D be the diagonal matrix with entries equal to the diagonal entries of A and let
We will use the fact that the eigenvalues are continuous in
, and show that if any eigenvalue moves from one of the unions to the other, then it must be outside all the discs for some 
, which is a contradiction.
The statement is true for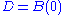
. The diagonal entries of 
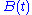are equal to that of A, thus the centers of the Gershgorin circles are the same, however their radii are t times that of A. Therefore the union of the corresponding k discs of 
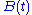is disjoint from the union of the remaining n-k for all t. The discs are closed, so the distance of the two unions for A is 
. The distance for 
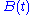is a decreasing function of t, so it is always at least d. Since the eigenvalues of 
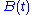are a continuous function of t, for any eigenvalue 
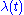of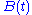 
in the union the k discs its distance 
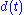from the union of the other n-k discs is also continuous. Obviously 
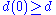, and assume 
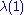lies in the union of the n-k discs. Then 
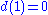, so there exists 
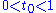such that 
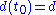. But this means 
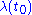lies outside the Gershgorin discs, which is impossible. Therefore 
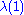lies in the union of the k discs, and the theorem is proven.
.
In this kind of problem, the error in the final result is usually of the same order of magnitude
as the error in the initial data multiplied by the condition number of A. For instance, if b is known to six decimal places and the condition number of A is 1000 then we can only be confident that x is accurate to three decimal places. For very high condition numbers, even very small errors due to rounding can be magnified to such an extent that the result is meaningless.
It would be good to reduce the condition number of A. This can be done by preconditioning: A matrix P such that P ≈ A−1 is constructed, and then the equation PAx = Pb is solved for x. Using the exact inverse of A would be nice but finding the inverse of a matrix is generally very difficult.
Now, since PA ≈ I where I is the identity matrix, the eigenvalues of PA should all be close to 1. By the Gerschgorin circle theorem, every eigenvalue of PA lies within a known area and so we can form a rough estimate of how good our choice of P was.
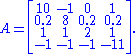
Starting with row one, we take the element on the diagonal, aii as the center for the disc. We then take the remaining elements in the row and apply the formula:
to obtain the following four discs:
The first two disks overlap and their union contains two eigenvalues. The third and fourth disks are disjoint from the others and contain one eigenvalue each.
Note that we can improve the accuracy of the last two discs by applying the formula to the corresponding columns of the matrix, obtaining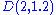
and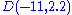 
.
The eigenvalues are 9.8218, 8.1478, 1.8995, −10.86
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Gershgorin circle theorem may be used to bound the spectrum of a square matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. It was first published by the Belarusian mathematician Semyon Aranovich Gershgorin
Semyon Aranovich Gershgorin
Semyon Aranovich Gershgorin was a Soviet mathematician. He began as a student at the Petrograd Technological Institute in 1923, became a Professor in 1930, and was given an appointment at the Leningrad Mechanical Engineering Institute in the same year...
in 1931. The spelling of S. A. Gershgorin's name has been transliterated in several different ways, including Geršgorin, Gerschgorin, Gershgorin and Hershhorn/Hirschhorn, the latter corresponding to the transliteration of the Yiddish spelling of his name, which is .
Statement and proof
Let A be a complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
n × n matrix, with entries
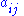. For i ∈ {1, …, n} let 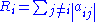be the sum of the absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
s of the non-diagonal entries in the ith row. Let D(aii, Ri) be the closed disc centered at aii with radius Ri. Such a disc is called a Gershgorin disc.
Theorem: Every eigenvalue of A lies within at least one of the Gershgorin discs D(aii, Ri).
Proof: Let λ be an eigenvalue of A and let x = (xj) be a corresponding eigenvector. Let i ∈ {1, …, n} be chosen so that |xi| = maxj |xj|. (That is to say, choose i so that xi is the largest (in absolute value) number in the vector x) Then |xi| > 0, otherwise x = 0. Since x is an eigenvector, Ax = λx, and thus:
So, splitting the sum, we get
We may then divide both sides by xi (choosing i as we explained we can be sure that xi ≠ 0) and take the absolute value to obtain
where the last inequality is valid because
Corollary: The eigenvalues of A must also lie within the Gershgorin discs Cj corresponding to the columns of A.
Proof: Apply the Theorem to AT.
Example For a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, the Gershgorin discs coincide with the spectrum. Conversely, if the Gershgorin discs coincide with the spectrum, the matrix is diagonal.
Discussion
One way to interpret this theorem is that if the off-diagonal entries of a square matrix over the complex numbers have small norms, the eigenvalues of the matrix cannot be "far from" the diagonal entries of the matrix. Therefore, by reducing the norms of off-diagonal entries one can attempt to approximate the eigenvalues of the matrix. Of course, diagonal entries may change in the process of minimizing off-diagonal entries.Strengthening of the theorem
If one of the discs is disjoint from the others then it contains exactly one eigenvalue. If however it meets another disc it is possible that it contains no eigenvalue. In the general case the theorem can be strengthened as follows:Theorem: If the union of k discs is disjoint from the union of the other n − k discs then the former union contains exactly k and the latter n − k eigenvalues of A.
Proof: Let D be the diagonal matrix with entries equal to the diagonal entries of A and let
We will use the fact that the eigenvalues are continuous in
, and show that if any eigenvalue moves from one of the unions to the other, then it must be outside all the discs for some , which is a contradiction.The statement is true for
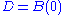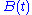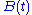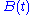. The diagonal entries of are equal to that of A, thus the centers of the Gershgorin circles are the same, however their radii are t times that of A. Therefore the union of the corresponding k discs of is disjoint from the union of the remaining n-k for all t. The discs are closed, so the distance of the two unions for A is . The distance for is a decreasing function of t, so it is always at least d. Since the eigenvalues of 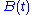are a continuous function of t, for any eigenvalue 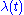of 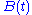in the union the k discs its distance 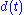from the union of the other n-k discs is also continuous. Obviously 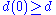, and assume 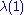lies in the union of the n-k discs. Then 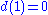, so there exists 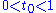such that 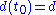. But this means 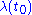lies outside the Gershgorin discs, which is impossible. Therefore 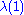lies in the union of the k discs, and the theorem is proven.Application
The Gershgorin circle theorem is useful in solving matrix equations of the form Ax = b for x where b is a vector and A is a matrix with a large condition numberCondition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
.
In this kind of problem, the error in the final result is usually of the same order of magnitude
Order of magnitude
An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
as the error in the initial data multiplied by the condition number of A. For instance, if b is known to six decimal places and the condition number of A is 1000 then we can only be confident that x is accurate to three decimal places. For very high condition numbers, even very small errors due to rounding can be magnified to such an extent that the result is meaningless.
It would be good to reduce the condition number of A. This can be done by preconditioning: A matrix P such that P ≈ A−1 is constructed, and then the equation PAx = Pb is solved for x. Using the exact inverse of A would be nice but finding the inverse of a matrix is generally very difficult.
Now, since PA ≈ I where I is the identity matrix, the eigenvalues of PA should all be close to 1. By the Gerschgorin circle theorem, every eigenvalue of PA lies within a known area and so we can form a rough estimate of how good our choice of P was.
Example
Use the Gerschgorin circle theorem to estimate the eigenvalues of: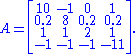Starting with row one, we take the element on the diagonal, aii as the center for the disc. We then take the remaining elements in the row and apply the formula:
to obtain the following four discs:
The first two disks overlap and their union contains two eigenvalues. The third and fourth disks are disjoint from the others and contain one eigenvalue each.
Note that we can improve the accuracy of the last two discs by applying the formula to the corresponding columns of the matrix, obtaining
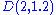and 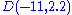.The eigenvalues are 9.8218, 8.1478, 1.8995, −10.86
See also
- For matrices with non-negative entries, see Perron–Frobenius theoremPerron–Frobenius theoremIn linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
. - Metzler matrix
- Doubly stochastic matrixDoubly stochastic matrixIn mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
- Muirhead's inequalityMuirhead's inequalityIn mathematics, Muirhead's inequality, named after Robert Franklin Muirhead, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means.-The "a-mean":For any real vectora=...
- Metzler matrix
- Hurwitz matrixHurwitz matrix-Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...
External links
- Eric W. Weisstein. "Gershgorin Circle Theorem." From MathWorld—A Wolfram Web Resource.
- Semyon Aranovich Gershgorin biography at MacTutor