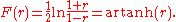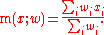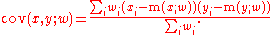Pearson product-moment correlation coefficient
Encyclopedia
In statistics
, the Pearson product-moment correlation coefficient (sometimes referred to as the PPMCC or PCCs, and typically denoted by r) is a measure of the correlation
(linear dependence) between two variables X and Y, giving a value between +1 and −1 inclusive. It is widely used in the sciences as a measure of the strength of linear dependence between two variables. It was developed by Karl Pearson
from a similar but slightly different idea introduced by Francis Galton
in the 1880s.
The correlation coefficient is sometimes called "Pearson's r."
of the two variables divided by the product of their standard deviations: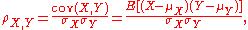
The above formula defines the population correlation coefficient, commonly represented by the Greek letter ρ (rho). Substituting estimates of the covariances and variances based on a sample gives the sample correlation coefficient, commonly denoted r :
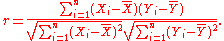
An equivalent expression gives the correlation coefficient as the mean of the products of the standard score
s. Based on a sample of paired data (Xi, Yi), the sample Pearson correlation coefficient is
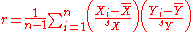
where
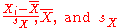
are the standard score
, sample mean
, and sample standard deviation
, respectively.
A key mathematical property of the Pearson correlation coefficient is that it is invariant
(up to a sign) to separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants, without changing the correlation coefficient (this fact holds for both the population and sample Pearson correlation coefficients). Note that more general linear transformations do change the correlation: see a later section for an application of this.
The Pearson correlation can be expressed in terms of uncentered moments. Since μX = E(X), σX2 = E[(X − E(X))2] = E(X2) − E2(X) and
likewise for Y, and since
the correlation can also be written as
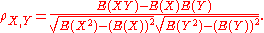
Alternative formulae for the sample Pearson correlation coefficient are also available:

The above formula suggests a convenient single-pass algorithm for calculating sample correlations, but, depending on the numbers involved, it can sometimes be numerically unstable
.
for which Y increases as X increases. A value of −1 implies that all data points lie on a line for which Y decreases as X increases. A value of 0 implies that there is no linear correlation between the variables.
More generally, note that (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative if Xi and Yi tend to lie on opposite sides of their respective means.
For uncentered data, the correlation coefficient corresponds with the cosine of the angle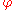 between both possible regression lines y=gx(x) and x=gy(y).
between both possible regression lines y=gx(x) and x=gy(y).
For centered data (i.e., data which have been shifted by the sample mean so as to have an average of zero), the correlation coefficient can also be viewed as the cosine of the angle
 between the two vectors of samples drawn from the two random variables (see below).
between the two vectors of samples drawn from the two random variables (see below).
Some practitioners prefer an uncentered (non-Pearson-compliant) correlation coefficient. See the example below for a comparison.
As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, 8) and y = (0.11, 0.12, 0.13, 0.15, 0.18).
By the usual procedure for finding the angle between two vectors (see dot product
between two vectors (see dot product
), the uncentered correlation coefficient is:
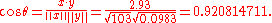
Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by E(x) = 3.8 and y by E(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which

as expected.
Several authors have offered guidelines for the interpretation of a correlation coefficient. However, all such criteria are in some ways arbitrary and should not be observed too strictly. The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.9 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences where there may be a greater contribution from complicating factors.
that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r. The other aim is to construct a confidence interval
around r that has a given probability of containing ρ.
) approach is to separately draw the i and the i′ "with replacement" from {1,..., n}; (ii) Construct a correlation coefficient r from the randomized data. To perform the permutation test, repeat (i) and (ii) a large number of times. The p-value
for the permutation test is one minus the proportion of the r values generated in step (ii) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here "larger" can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided
or one-sided
test is desired.
The bootstrap
can be used to construct confidence intervals for Pearson's correlation coefficient. In the "non-parametric" bootstrap, n pairs (xi, yi) are resampled "with replacement" from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution
of the statistic. A 95% confidence interval
for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile
of the resampled r values.
of Pearson's correlation coefficient approximately follows Student's t-distribution with degrees of freedom N − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable.
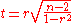
has a Student's t-distribution in the null case (zero correlation). This also holds approximately even if the observed values are non-normal, provided sample sizes are not very small. For constructing confidence intervals and performing power analyses, the inverse of this transformation is also needed:
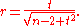
Alternatively, large sample approaches can be used.
Early work on the distribution of the sample correlation coefficient was carried out by R. A. Fisher
and A. K. Gayen.
Another early paper provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
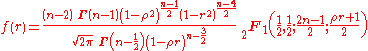
where is the Gamma function
is the Gamma function
,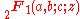 is the Gaussian hypergeometric function.
is the Gaussian hypergeometric function.
Note that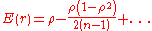 , therefore r is a biased estimator of
, therefore r is a biased estimator of 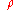 . An approximate unbiased estimator can be obtained by solving the equation
. An approximate unbiased estimator can be obtained by solving the equation  for
for 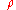 . However, the solution,
. However, the solution, 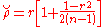 , is suboptimal. An unbiased estimator, with minimum variance for large values of n, with a bias of order
, is suboptimal. An unbiased estimator, with minimum variance for large values of n, with a bias of order 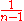 , can be obtained by maximizing
, can be obtained by maximizing 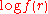 , i.e.
, i.e. 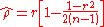 .
.
In the special case when , the distribution can be written as:
, the distribution can be written as:
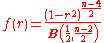
where is the Beta function.
is the Beta function.
:
If F(r) is the Fisher transformation of r, and n is the sample size, then F(r) approximately follows a normal distribution with
 and standard error
and standard error 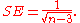
Thus, a z-score
is
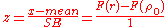
under the null hypothesis
of that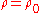 , given the assumption that the sample pairs are independent and identically distributed and follow a bivariate normal distribution. Thus an approximate p-value
, given the assumption that the sample pairs are independent and identically distributed and follow a bivariate normal distribution. Thus an approximate p-value
can be obtained from a normal probability table. For example, if z = 2.2 is observed and a two-sided p-value is desired to test the null hypothesis that , the p-value is 2·Φ(−2.2) = 0.028, where Φ is the standard normal cumulative distribution function
, the p-value is 2·Φ(−2.2) = 0.028, where Φ is the standard normal cumulative distribution function
.
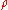 ):
):
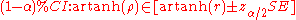
The inverse Fisher transformation bring the interval back to the correlation scale.
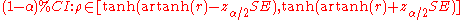
For example, suppose we observe r = 0.3 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.30952, so the confidence interval on the transformed scale is 0.30952 ± 1.96/√47, or (0.023624, 0.595415). Converting back to the correlation scale yields (0.024, 0.534).
, estimates the fraction of the variance in Y that is explained by X in a simple linear regression
. As a starting point, the total variation in the Yi around their average value can be decomposed as follows
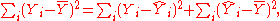
where the are the fitted values from the regression analysis. This can be rearranged to give
are the fitted values from the regression analysis. This can be rearranged to give
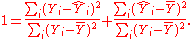
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between and
and  is zero. Thus, the sample correlation coefficient between the observed and fitted response values in the regression can be written
is zero. Thus, the sample correlation coefficient between the observed and fitted response values in the regression can be written
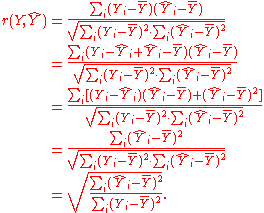
Thus
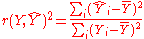
is the proportion of variance in Y explained by a linear function of X.
, and therefore exists for any bivariate probability distribution
for which the population
covariance
is defined and the marginal
population variances are defined and are non-zero. Some probability distributions such as the Cauchy distribution
have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution
, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
The sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient for bivariate normal data, and is asymptotically
unbiased
and efficient
, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient if the data are normal and the sample size is moderate or large. For non-normal populations, the sample correlation coefficient remains approximately unbiased, but may not be efficient. The sample correlation coefficient is a consistent estimator
of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers
can be applied).
, so its value can be misleading if outlier
s are present. Specifically, the PMCC is neither distributionally robust, nor outlier resistant (see Robust statistics#Definition). Inspection of the scatterplot
between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson's correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation
can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap
can be applied to construct confidence intervals, and permutation tests
can be applied to carry out hypothesis tests. These non-parametric
approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.
A corresponding result exists for sample correlations, in which the sample correlation is reduced to zero. Suppose a vector of n random variables is sampled m times. Let X be a matrix where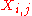 is the jth variable of sample i. Let
is the jth variable of sample i. Let  be an m by m square matrix with every element 1. Then D is the data transformed so every random variable has zero mean, and T is the data transformed so all variables have zero mean and zero correlation with all other variables - the moment matrix of T will be the identity matrix. This has to be further divided by the standard deviation to get unit variance. The transformed variables will be uncorrelated, even though they may not be independent
be an m by m square matrix with every element 1. Then D is the data transformed so every random variable has zero mean, and T is the data transformed so all variables have zero mean and zero correlation with all other variables - the moment matrix of T will be the identity matrix. This has to be further divided by the standard deviation to get unit variance. The transformed variables will be uncorrelated, even though they may not be independent
.
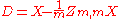
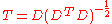
where an exponent of -1/2 represents the matrix square root of the inverse of a matrix. The covariance matrix of T will be the identity matrix. If a new data sample x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
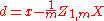

This decorrelation is related to Principal Components Analysis
for multivariate data.
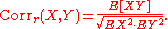
The reflective correlation is symmetric, but it is not invariant under translation:
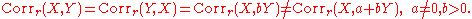
The sample reflective correlation is

The weighted version of the sample reflective correlation is
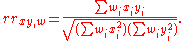
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Pearson product-moment correlation coefficient (sometimes referred to as the PPMCC or PCCs, and typically denoted by r) is a measure of the correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
(linear dependence) between two variables X and Y, giving a value between +1 and −1 inclusive. It is widely used in the sciences as a measure of the strength of linear dependence between two variables. It was developed by Karl Pearson
Karl Pearson
Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
from a similar but slightly different idea introduced by Francis Galton
Francis Galton
Sir Francis Galton /ˈfrɑːnsɪs ˈgɔːltn̩/ FRS , cousin of Douglas Strutt Galton, half-cousin of Charles Darwin, was an English Victorian polymath: anthropologist, eugenicist, tropical explorer, geographer, inventor, meteorologist, proto-geneticist, psychometrician, and statistician...
in the 1880s.
The correlation coefficient is sometimes called "Pearson's r."
Definition
Pearson's correlation coefficient between two variables is defined as the covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
of the two variables divided by the product of their standard deviations:
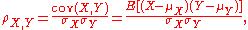
The above formula defines the population correlation coefficient, commonly represented by the Greek letter ρ (rho). Substituting estimates of the covariances and variances based on a sample gives the sample correlation coefficient, commonly denoted r :
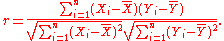
An equivalent expression gives the correlation coefficient as the mean of the products of the standard score
Standard score
In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
s. Based on a sample of paired data (Xi, Yi), the sample Pearson correlation coefficient is
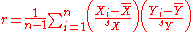
where
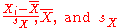
are the standard score
Standard score
In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
, sample mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, and sample standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
, respectively.
Mathematical properties
The absolute value of both the sample and population Pearson correlation coefficients are less than or equal to 1. Correlations equal to 1 or -1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).A key mathematical property of the Pearson correlation coefficient is that it is invariant
Invariant estimator
In statistics, the concept of being an invariant estimator is a criterion that can be used to compare the properties of different estimators for the same quantity. It is a way of formalising the idea that an estimator should have certain intuitively appealing qualities...
(up to a sign) to separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants, without changing the correlation coefficient (this fact holds for both the population and sample Pearson correlation coefficients). Note that more general linear transformations do change the correlation: see a later section for an application of this.
The Pearson correlation can be expressed in terms of uncentered moments. Since μX = E(X), σX2 = E[(X − E(X))2] = E(X2) − E2(X) and
likewise for Y, and since
the correlation can also be written as
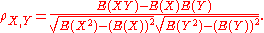
Alternative formulae for the sample Pearson correlation coefficient are also available:

The above formula suggests a convenient single-pass algorithm for calculating sample correlations, but, depending on the numbers involved, it can sometimes be numerically unstable
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
.
Interpretation
The correlation coefficient ranges from −1 to 1. A value of 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a lineLine (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
for which Y increases as X increases. A value of −1 implies that all data points lie on a line for which Y decreases as X increases. A value of 0 implies that there is no linear correlation between the variables.
More generally, note that (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative if Xi and Yi tend to lie on opposite sides of their respective means.
Geometric interpretation
]For uncentered data, the correlation coefficient corresponds with the cosine of the angle
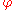 between both possible regression lines y=gx(x) and x=gy(y).
between both possible regression lines y=gx(x) and x=gy(y).For centered data (i.e., data which have been shifted by the sample mean so as to have an average of zero), the correlation coefficient can also be viewed as the cosine of the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
 between the two vectors of samples drawn from the two random variables (see below).
between the two vectors of samples drawn from the two random variables (see below).Some practitioners prefer an uncentered (non-Pearson-compliant) correlation coefficient. See the example below for a comparison.
As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, 8) and y = (0.11, 0.12, 0.13, 0.15, 0.18).
By the usual procedure for finding the angle
 between two vectors (see dot product
between two vectors (see dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
), the uncentered correlation coefficient is:
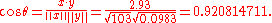
Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by E(x) = 3.8 and y by E(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which

as expected.
Interpretation of the size of a correlation
| Correlation | Negative | Positive |
|---|---|---|
| None | −0.09 to 0.0 | 0.0 to 0.09 |
| Small | −0.3 to −0.1 | 0.1 to 0.3 |
| Medium | −0.5 to −0.3 | 0.3 to 0.5 |
| Strong | −1.0 to −0.5 | 0.5 to 1.0 |
Several authors have offered guidelines for the interpretation of a correlation coefficient. However, all such criteria are in some ways arbitrary and should not be observed too strictly. The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.9 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences where there may be a greater contribution from complicating factors.
Inference
Statistical inference based on Pearson's correlation coefficient often focuses on one of the following two aims. One aim is to test the null hypothesisNull hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r. The other aim is to construct a confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
around r that has a given probability of containing ρ.
Randomization approaches
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson's correlation coefficient involves the following two steps: (i) using the original paired data (xi, yi), randomly redefine the pairs to create a new data set (xi, yi′), where the i′ are a permutation of the set {1,...,n}. The permutation i′ is selected randomly, with equal probabilities placed on all n! possible permutations. This is equivalent to drawing the i′ randomly "without replacement" from the set {1,..., n}. A closely related and equally justified (bootstrappingBootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
) approach is to separately draw the i and the i′ "with replacement" from {1,..., n}; (ii) Construct a correlation coefficient r from the randomized data. To perform the permutation test, repeat (i) and (ii) a large number of times. The p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
for the permutation test is one minus the proportion of the r values generated in step (ii) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here "larger" can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided
Two-tailed test
The two-tailed test is a statistical test used in inference, in which a given statistical hypothesis, H0 , will be rejected when the value of the test statistic is either sufficiently small or sufficiently large...
or one-sided
Two-tailed test
The two-tailed test is a statistical test used in inference, in which a given statistical hypothesis, H0 , will be rejected when the value of the test statistic is either sufficiently small or sufficiently large...
test is desired.
The bootstrap
Bootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
can be used to construct confidence intervals for Pearson's correlation coefficient. In the "non-parametric" bootstrap, n pairs (xi, yi) are resampled "with replacement" from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution
Sampling distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
of the statistic. A 95% confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile
Percentile
In statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...
of the resampled r values.
Approaches based on mathematical approximations
For approximately Gaussian data, the sampling distributionSampling distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
of Pearson's correlation coefficient approximately follows Student's t-distribution with degrees of freedom N − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable.
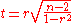
has a Student's t-distribution in the null case (zero correlation). This also holds approximately even if the observed values are non-normal, provided sample sizes are not very small. For constructing confidence intervals and performing power analyses, the inverse of this transformation is also needed:
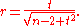
Alternatively, large sample approaches can be used.
Early work on the distribution of the sample correlation coefficient was carried out by R. A. Fisher
and A. K. Gayen.
Another early paper provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
Exact distribution for Gaussian data
The exact distribution for the sample correlation of a normal bivariate is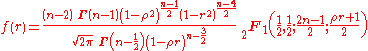
where
 is the Gamma function
is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
,
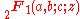 is the Gaussian hypergeometric function.
is the Gaussian hypergeometric function.Note that
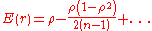 , therefore r is a biased estimator of
, therefore r is a biased estimator of 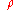 . An approximate unbiased estimator can be obtained by solving the equation
. An approximate unbiased estimator can be obtained by solving the equation  for
for 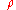 . However, the solution,
. However, the solution, 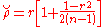 , is suboptimal. An unbiased estimator, with minimum variance for large values of n, with a bias of order
, is suboptimal. An unbiased estimator, with minimum variance for large values of n, with a bias of order 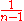 , can be obtained by maximizing
, can be obtained by maximizing 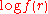 , i.e.
, i.e. 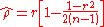 .
.In the special case when
 , the distribution can be written as:
, the distribution can be written as: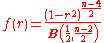
where
 is the Beta function.
is the Beta function.Fisher Transformation
In practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformationFisher transformation
In statistics, hypotheses about the value of the population correlation coefficient ρ between variables X and Y can be tested using the Fisher transformation applied to the sample correlation coefficient r.-Definition:...
:
If F(r) is the Fisher transformation of r, and n is the sample size, then F(r) approximately follows a normal distribution with
 and standard error
and standard error 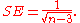
Thus, a z-score
Standard score
In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
is
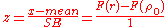
under the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
of that
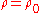 , given the assumption that the sample pairs are independent and identically distributed and follow a bivariate normal distribution. Thus an approximate p-value
, given the assumption that the sample pairs are independent and identically distributed and follow a bivariate normal distribution. Thus an approximate p-valueP-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
can be obtained from a normal probability table. For example, if z = 2.2 is observed and a two-sided p-value is desired to test the null hypothesis that
 , the p-value is 2·Φ(−2.2) = 0.028, where Φ is the standard normal cumulative distribution function
, the p-value is 2·Φ(−2.2) = 0.028, where Φ is the standard normal cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
.
Confidence Intervals
To obtain a confidence interval for ρ, we first compute a confidence interval for F(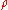 ):
):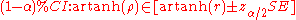
The inverse Fisher transformation bring the interval back to the correlation scale.
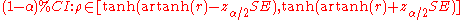
For example, suppose we observe r = 0.3 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.30952, so the confidence interval on the transformed scale is 0.30952 ± 1.96/√47, or (0.023624, 0.595415). Converting back to the correlation scale yields (0.024, 0.534).
Pearson's correlation and least squares regression analysis
The square of the sample correlation coefficient, which is also known as the coefficient of determinationCoefficient of determination
In statistics, the coefficient of determination R2 is used in the context of statistical models whose main purpose is the prediction of future outcomes on the basis of other related information. It is the proportion of variability in a data set that is accounted for by the statistical model...
, estimates the fraction of the variance in Y that is explained by X in a simple linear regression
Simple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
. As a starting point, the total variation in the Yi around their average value can be decomposed as follows
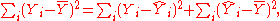
where the
 are the fitted values from the regression analysis. This can be rearranged to give
are the fitted values from the regression analysis. This can be rearranged to give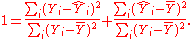
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between
 and
and  is zero. Thus, the sample correlation coefficient between the observed and fitted response values in the regression can be written
is zero. Thus, the sample correlation coefficient between the observed and fitted response values in the regression can be written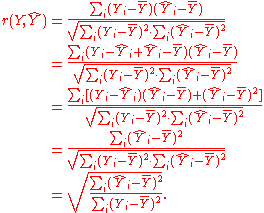
Thus
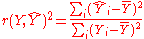
is the proportion of variance in Y explained by a linear function of X.
Existence
The population Pearson correlation coefficient is defined in terms of momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
, and therefore exists for any bivariate probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
for which the population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
is defined and the marginal
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
population variances are defined and are non-zero. Some probability distributions such as the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution
Heavy-tailed distribution
In probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution...
, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
Large sample properties
In the case of the bivariate normal distribution the population Pearson correlation coefficient characterizes the joint distribution as long as the marginal means and variances are known. For most other bivariate distributions this is not true. Nevertheless, the correlation coefficient is highly informative about the degree of linear dependence between two random quantities regardless of whether their joint distribution is normal.The sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient for bivariate normal data, and is asymptotically
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
unbiased
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
and efficient
Efficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient if the data are normal and the sample size is moderate or large. For non-normal populations, the sample correlation coefficient remains approximately unbiased, but may not be efficient. The sample correlation coefficient is a consistent estimator
Consistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
can be applied).
Robustness
Like many commonly used statistics, the sample statistic r is not robustRobust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
, so its value can be misleading if outlier
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
s are present. Specifically, the PMCC is neither distributionally robust, nor outlier resistant (see Robust statistics#Definition). Inspection of the scatterplot
Scatterplot
A scatter plot or scattergraph is a type of mathematical diagram using Cartesian coordinates to display values for two variables for a set of data....
between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson's correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation
Fisher transformation
In statistics, hypotheses about the value of the population correlation coefficient ρ between variables X and Y can be tested using the Fisher transformation applied to the sample correlation coefficient r.-Definition:...
can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap
Bootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
can be applied to construct confidence intervals, and permutation tests
Resampling (statistics)
In statistics, resampling is any of a variety of methods for doing one of the following:# Estimating the precision of sample statistics by using subsets of available data or drawing randomly with replacement from a set of data points # Exchanging labels on data points when performing significance...
can be applied to carry out hypothesis tests. These non-parametric
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.
Calculating a weighted correlation
Suppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),- Weighted mean:
- Weighted covariance
- Weighted correlation
Removing correlation
It is always possible to remove the correlation between random variables with a linear transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.A corresponding result exists for sample correlations, in which the sample correlation is reduced to zero. Suppose a vector of n random variables is sampled m times. Let X be a matrix where
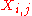 is the jth variable of sample i. Let
is the jth variable of sample i. Let  be an m by m square matrix with every element 1. Then D is the data transformed so every random variable has zero mean, and T is the data transformed so all variables have zero mean and zero correlation with all other variables - the moment matrix of T will be the identity matrix. This has to be further divided by the standard deviation to get unit variance. The transformed variables will be uncorrelated, even though they may not be independent
be an m by m square matrix with every element 1. Then D is the data transformed so every random variable has zero mean, and T is the data transformed so all variables have zero mean and zero correlation with all other variables - the moment matrix of T will be the identity matrix. This has to be further divided by the standard deviation to get unit variance. The transformed variables will be uncorrelated, even though they may not be independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
.
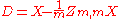
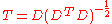
where an exponent of -1/2 represents the matrix square root of the inverse of a matrix. The covariance matrix of T will be the identity matrix. If a new data sample x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
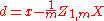

This decorrelation is related to Principal Components Analysis
Principal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
for multivariate data.
Reflective correlation
The reflective correlation is a variant of Pearson's correlation in which the data are not centered around their mean values. The population reflective correlation is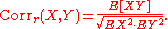
The reflective correlation is symmetric, but it is not invariant under translation:
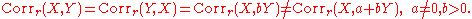
The sample reflective correlation is

The weighted version of the sample reflective correlation is
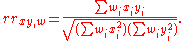
See also
- Correlation and dependence
- Spearman's rank correlation coefficientSpearman's rank correlation coefficientIn statistics, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman and often denoted by the Greek letter \rho or as r_s, is a non-parametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can...
- Association (statistics)Association (statistics)In statistics, an association is any relationship between two measured quantities that renders them statistically dependent. The term "association" refers broadly to any such relationship, whereas the narrower term "correlation" refers to a linear relationship between two quantities.There are many...
- Disattenuation