
Bias of an estimator
Encyclopedia
In statistics
, bias (or bias function) of an estimator
is the difference between this estimator's expected value
and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.
In ordinary English, the term bias is pejorative
. In statistics, there are problems for which it may be good to use an estimator with a small, but nonzero, bias. In some cases, an estimator with a small bias may have lesser mean squared error
or be median
-unbiased (rather than mean
-unbiased, the standard unbiasedness property). The property of median-unbiasedness is invariant under transformations, while the property of mean-unbiasedness may be lost under nonlinear transformations.
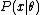 , and a statistic θ^ which serves as an estimator
, and a statistic θ^ which serves as an estimator
of θ based on any observed data . That is, we assume that our data follows some unknown distribution
. That is, we assume that our data follows some unknown distribution 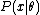 (where
(where 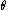 is a fixed constant that is part of this distribution, but is unknown), and then we construct some estimator
is a fixed constant that is part of this distribution, but is unknown), and then we construct some estimator 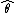 that maps observed data to values that we hope are close to
that maps observed data to values that we hope are close to 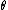 . Then the bias of this estimator is defined to be
. Then the bias of this estimator is defined to be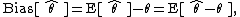
where denotes expected value
over the distribution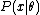 , i.e. averaging over all possible observations
, i.e. averaging over all possible observations  .
.
An estimator is said to be unbiased if its bias is equal to zero for all values of parameter θ.
There are more general notions of bias and unbiasedness. What this article calls "bias" is called "mean-bias", to distinguish mean-bias from the other notions, the notable ones being "median-unbiased" estimators. The general theory of unbiased estimators is briefly discussed near the end of this article.
In a simulation experiment concerning the properties of an estimator, the bias of the estimator may be assessed using the mean signed difference.
μ and variance
σ2. If the sample mean and uncorrected sample variance are defined as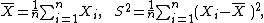
then S2 is a biased estimator of σ2, because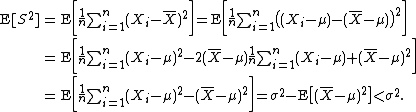
In other words, the expected value of the uncorrected sample variance does not equal the population variance σ2, unless multiplied by a normalization factor. The sample mean, on the other hand, is an unbiased estimator of the population mean μ.
The reason that S2 is biased stems from the fact that the sample mean is an ordinary least squares
(OLS) estimator for μ: It is such a number that makes the sum Σ(Xi − μ)2 as small as possible. That is, when any other number is plugged into this sum, the sum can only increase. In particular, the choice m = μ gives, first (or most outcomes)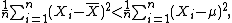
and then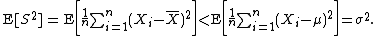
Note that the usual definition of sample variance is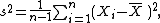
and this is an unbiased estimator of the population variance. This can be seen by noting the following formula for the term in the inequality for the expectation of the uncorrected sample variance above: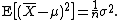
The ratio between the biased (uncorrected) and unbiased estimates of the variance is known as Bessel's correction
.
:: Suppose X has a Poisson distribution with expectation λ. Suppose it is desired to estimate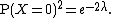
(For example, when incoming calls at a telephone switchboard are modeled as a Poisson process, and λ is the average number of calls per minute, then e−2λ is the probability that no calls arrive in the next two minutes.)
Since the expectation of an unbiased estimator δ(X) is equal to the estimand, i.e.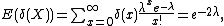
the only function of the data constituting an unbiased estimator is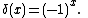
To see this, note that when decomposing e−λ from the above expression for expectation, the sum that is left is a Taylor series
expansion of e−λ as well, yielding e−λe−λ = e−2λ (see Characterizations of the exponential function
).
If the observed value of X is 100, then the estimate is 1, although the true value of the quantity being estimated is very likely to be near 0, which is the opposite extreme. And, if X is observed to be 101, then the estimate is even more absurd: It is −1, although the quantity being estimated must be positive.
The (biased) maximum likelihood estimator
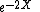
is far better than this unbiased estimator. Not only is its value always positive but it is also more accurate in the sense that its mean squared error
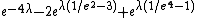
is smaller; compare the unbiased estimator's MSE of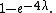
The MSEs are functions of the true value λ. The bias of the maximum-likelihood estimator is: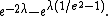
Further properties of median-unbiased estimators have been noted by Lehmann, Birnbaum, van der Vaart and Pfanzagl. In particular, median-unbiased estimators exist in cases where mean-unbiased and maximum-likelihood
estimators do not exist. Besides being invariant under one-to-one transformations
, median-unbiased estimators have surprising robustness
.
, as observed by Gauss
. A median
-unbiased estimator minimizes the risk with respect to the absolute
loss function, as observed by Laplace. Other loss functions are used in statistical theory
, particularly in robust statistics
.
of the unbiased estimator of the population variance
is not a mean-unbiased estimator of the population standard deviation
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, bias (or bias function) of an estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
is the difference between this estimator's expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.
In ordinary English, the term bias is pejorative
Pejorative
Pejoratives , including name slurs, are words or grammatical forms that connote negativity and express contempt or distaste. A term can be regarded as pejorative in some social groups but not in others, e.g., hacker is a term used for computer criminals as well as quick and clever computer experts...
. In statistics, there are problems for which it may be good to use an estimator with a small, but nonzero, bias. In some cases, an estimator with a small bias may have lesser mean squared error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
or be median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
-unbiased (rather than mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
-unbiased, the standard unbiasedness property). The property of median-unbiasedness is invariant under transformations, while the property of mean-unbiasedness may be lost under nonlinear transformations.
Definition
Suppose we have a statistical model parameterized by θ giving rise to a probability distribution for observed data,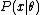 , and a statistic θ^ which serves as an estimator
, and a statistic θ^ which serves as an estimatorEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of θ based on any observed data
 . That is, we assume that our data follows some unknown distribution
. That is, we assume that our data follows some unknown distribution 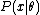 (where
(where 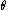 is a fixed constant that is part of this distribution, but is unknown), and then we construct some estimator
is a fixed constant that is part of this distribution, but is unknown), and then we construct some estimator 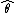 that maps observed data to values that we hope are close to
that maps observed data to values that we hope are close to 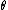 . Then the bias of this estimator is defined to be
. Then the bias of this estimator is defined to be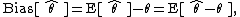
where denotes expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
over the distribution
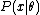 , i.e. averaging over all possible observations
, i.e. averaging over all possible observations  .
.An estimator is said to be unbiased if its bias is equal to zero for all values of parameter θ.
There are more general notions of bias and unbiasedness. What this article calls "bias" is called "mean-bias", to distinguish mean-bias from the other notions, the notable ones being "median-unbiased" estimators. The general theory of unbiased estimators is briefly discussed near the end of this article.
In a simulation experiment concerning the properties of an estimator, the bias of the estimator may be assessed using the mean signed difference.
Sample variance
Suppose X1, ..., Xn are independent and identically distributed (i.i.d) random variables with expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ2. If the sample mean and uncorrected sample variance are defined as
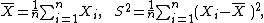
then S2 is a biased estimator of σ2, because
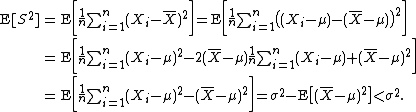
In other words, the expected value of the uncorrected sample variance does not equal the population variance σ2, unless multiplied by a normalization factor. The sample mean, on the other hand, is an unbiased estimator of the population mean μ.
The reason that S2 is biased stems from the fact that the sample mean is an ordinary least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
(OLS) estimator for μ: It is such a number that makes the sum Σ(Xi − μ)2 as small as possible. That is, when any other number is plugged into this sum, the sum can only increase. In particular, the choice m = μ gives, first (or most outcomes)
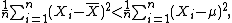
and then
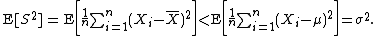
Note that the usual definition of sample variance is
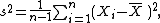
and this is an unbiased estimator of the population variance. This can be seen by noting the following formula for the term in the inequality for the expectation of the uncorrected sample variance above:
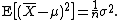
The ratio between the biased (uncorrected) and unbiased estimates of the variance is known as Bessel's correction
Bessel's correction
In statistics, Bessel's correction, named after Friedrich Bessel, is the use of n − 1 instead of n in the formula for the sample variance and sample standard deviation, where n is the number of observations in a sample: it corrects the bias in the estimation of the population variance,...
.
Estimating a Poisson probability
A far more extreme case of a biased estimator being better than any unbiased estimator arises from the Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
:: Suppose X has a Poisson distribution with expectation λ. Suppose it is desired to estimate
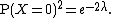
(For example, when incoming calls at a telephone switchboard are modeled as a Poisson process, and λ is the average number of calls per minute, then e−2λ is the probability that no calls arrive in the next two minutes.)
Since the expectation of an unbiased estimator δ(X) is equal to the estimand, i.e.
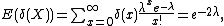
the only function of the data constituting an unbiased estimator is
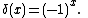
To see this, note that when decomposing e−λ from the above expression for expectation, the sum that is left is a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion of e−λ as well, yielding e−λe−λ = e−2λ (see Characterizations of the exponential function
Characterizations of the exponential function
In mathematics, the exponential function can be characterized in many ways. The following characterizations are most common. This article discusses why each characterization makes sense, and why the characterizations are independent of and equivalent to each other...
).
If the observed value of X is 100, then the estimate is 1, although the true value of the quantity being estimated is very likely to be near 0, which is the opposite extreme. And, if X is observed to be 101, then the estimate is even more absurd: It is −1, although the quantity being estimated must be positive.
The (biased) maximum likelihood estimator
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
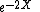
is far better than this unbiased estimator. Not only is its value always positive but it is also more accurate in the sense that its mean squared error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
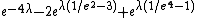
is smaller; compare the unbiased estimator's MSE of
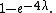
The MSEs are functions of the true value λ. The bias of the maximum-likelihood estimator is:
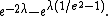
Maximum of a discrete uniform distribution
The bias of maximum-likelihood estimators can be substantial. Consider a case where n tickets numbered from 1 through to n are placed in a box and one is selected at random, giving a value X. If n is unknown, then the maximum-likelihood estimator of n is X, even though the expectation of X is only (n + 1)/2; we can be certain only that n is at least X and is probably more. In this case, the natural unbiased estimator is 2X − 1.Median-unbiased estimators
The theory of median-unbiased estimators was revived by George W. Brown in 1947:An estimate of a one-dimensional parameter θ will be said to be median-unbiased, if, for fixed θ, the median of the distribution of the estimate is at the value θ; i.e., the estimate underestimates just as often as it overestimates. This requirement seems for most purposes to accomplish as much as the mean-unbiased requirement and has the additional property that it is invariantInvariant estimatorIn statistics, the concept of being an invariant estimator is a criterion that can be used to compare the properties of different estimators for the same quantity. It is a way of formalising the idea that an estimator should have certain intuitively appealing qualities...
under one-to-one transformationInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
.
Further properties of median-unbiased estimators have been noted by Lehmann, Birnbaum, van der Vaart and Pfanzagl. In particular, median-unbiased estimators exist in cases where mean-unbiased and maximum-likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimators do not exist. Besides being invariant under one-to-one transformations
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, median-unbiased estimators have surprising robustness
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
.
Bias with respect to other loss functions
Any mean-unbiased estimator minimizes the risk (expected loss) with respect to the squared-error loss functionLoss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
, as observed by Gauss
Gauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
. A median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
-unbiased estimator minimizes the risk with respect to the absolute
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
loss function, as observed by Laplace. Other loss functions are used in statistical theory
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
, particularly in robust statistics
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
.
Effect of transformations
Note that, when a transformation is applied to a mean-unbiased estimator, the result need not be a mean-unbiased estimator of its corresponding population statistic. That is, for a non-linear function f and a mean-unbiased estimator U of a parameter p, the composite estimator f(U) need not be a mean-unbiased estimator of f(p). For example, the square rootSquare root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the unbiased estimator of the population variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is not a mean-unbiased estimator of the population standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
.
See also
- Omitted-variable biasOmitted-variable biasIn statistics, omitted-variable bias occurs when a model is created which incorrectly leaves out one or more important causal factors. The 'bias' is created when the model compensates for the missing factor by over- or under-estimating one of the other factors.More specifically, OVB is the bias...
- Consistent estimatorConsistent estimatorIn statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
- Estimation theoryEstimation theoryEstimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
- Expected loss
- Expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
- Loss functionLoss functionIn statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
- MedianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
- Statistical decision theory

