
Sampling distribution
Encyclopedia
In statistics
, a sampling distribution or finite-sample distribution is the probability distribution
of a given statistic
based on a random sample
. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference
. More specifically, they allow analytical considerations to be based on the sampling distribution of a statistic, rather than on the joint probability distribution of all the individual sample values.
of that statistic
, considered as a random variable
, when derived from a random sample
of size n. It may be considered as the distribution of the statistic for all possible samples from the same population of a given size. The sampling distribution depends on the underlying distribution
of the population, the statistic being considered, the sampling procedure employed and the sample size used. There is often considerable interest in whether the sampling distribution can be approximated by an asymptotic distribution
, which corresponds to the limiting case as n → ∞.
For example, consider a normal population with mean μ and variance σ². Assume we repeatedly take samples of a given size from this population and calculate the arithmetic mean
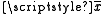 for each sample — this statistic is called the sample mean. Each sample has its own average value, and the distribution of these averages is called the "sampling distribution of the sample mean". This distribution is normal
for each sample — this statistic is called the sample mean. Each sample has its own average value, and the distribution of these averages is called the "sampling distribution of the sample mean". This distribution is normal 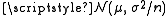 since the underlying population is normal, although sampling distributions may also often be close to normal even when the population distribution is not (see central limit theorem
since the underlying population is normal, although sampling distributions may also often be close to normal even when the population distribution is not (see central limit theorem
). An alternative to the sample mean is the sample median
. When calculated from the same population, it has a different sampling distribution to that of the mean and is generally not normal (but it may be close for large sample sizes).
The mean of a sample from a population having a normal distribution is an example of a simple statistic taken from one of the simplest statistical population
s. For other statistics and other populations the formulas are more complicated, and often they don't exist in closed-form
. In such cases the sampling distributions may be approximated through Monte-Carlo simulations, bootstrap
methods, or asymptotic distribution
theory.
of the sampling distribution of the statistic is referred to as the
standard error
of that quantity. For the case where the statistic is the sample mean, and samples are uncorrelated, the standard error is:
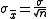
where is the standard deviation of the population distribution of that quantity
is the standard deviation of the population distribution of that quantity
and n is the size (number of items) in the sample.
An important implication of this formula is that the sample size must be quadrupled (multiplied by 4) to achieve half (1/2) the measurement error. When designing
statistical studies where cost is a factor, this may have a role in
understanding cost-benefit tradeoffs.
, the idea of a sufficient statistic provides the basis of choosing a statistic (as a function of the sample data points) in such a way that no information is lost by replacing the full probabilistic description of the sample with the sampling distribution of the selected statistic.
In frequentist inference
, for example in the development of a statistical hypothesis test or a confidence interval
, the availability of the sampling distribution of a statistic (or an approximation to this in the form of an asymptotic distribution
) can allow the ready formulation of such procedures, whereas the development of procedures starting from the joint distribution of the sample would be less straightforward.
In Bayesian inference
, when the sampling distribution of a statistic is available, one can consider replacing the final outcome of such procedures, specifically the conditional distribution
s of any unknown quantities given the sample data, by the conditional distribution
s of any unknown quantities given selected sample statistics. Such a procedure would involve the sampling distribution of the statistics. The results would be identical provided the statistics chosen are jointly sufficient statistics.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a sampling distribution or finite-sample distribution is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of a given statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
based on a random sample
Random sample
In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...
. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
. More specifically, they allow analytical considerations to be based on the sampling distribution of a statistic, rather than on the joint probability distribution of all the individual sample values.
Introduction
The sampling distribution of a statistic is the distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of that statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
, considered as a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, when derived from a random sample
Random sample
In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...
of size n. It may be considered as the distribution of the statistic for all possible samples from the same population of a given size. The sampling distribution depends on the underlying distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the population, the statistic being considered, the sampling procedure employed and the sample size used. There is often considerable interest in whether the sampling distribution can be approximated by an asymptotic distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
, which corresponds to the limiting case as n → ∞.
For example, consider a normal population with mean μ and variance σ². Assume we repeatedly take samples of a given size from this population and calculate the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
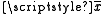 for each sample — this statistic is called the sample mean. Each sample has its own average value, and the distribution of these averages is called the "sampling distribution of the sample mean". This distribution is normal
for each sample — this statistic is called the sample mean. Each sample has its own average value, and the distribution of these averages is called the "sampling distribution of the sample mean". This distribution is normal 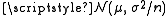 since the underlying population is normal, although sampling distributions may also often be close to normal even when the population distribution is not (see central limit theorem
since the underlying population is normal, although sampling distributions may also often be close to normal even when the population distribution is not (see central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
). An alternative to the sample mean is the sample median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
. When calculated from the same population, it has a different sampling distribution to that of the mean and is generally not normal (but it may be close for large sample sizes).
The mean of a sample from a population having a normal distribution is an example of a simple statistic taken from one of the simplest statistical population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
s. For other statistics and other populations the formulas are more complicated, and often they don't exist in closed-form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
. In such cases the sampling distributions may be approximated through Monte-Carlo simulations, bootstrap
Bootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
methods, or asymptotic distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
theory.
Standard error
The standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the sampling distribution of the statistic is referred to as the
standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
of that quantity. For the case where the statistic is the sample mean, and samples are uncorrelated, the standard error is:
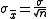
where
 is the standard deviation of the population distribution of that quantity
is the standard deviation of the population distribution of that quantityand n is the size (number of items) in the sample.
An important implication of this formula is that the sample size must be quadrupled (multiplied by 4) to achieve half (1/2) the measurement error. When designing
statistical studies where cost is a factor, this may have a role in
understanding cost-benefit tradeoffs.
Examples
| Population | Statistic | Sampling distribution |
|---|---|---|
Normal: 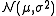 |
Sample mean 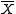 from samples of size n from samples of size n |
 |
Bernoulli:  |
Sample proportion of "successful trials"  |
 |
Two independent normal populations: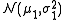 and and  |
Difference between sample means, 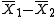 |
 |
| Any absolutely continuous distribution F with density ƒ | Median Median In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to... 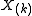 from a sample of size n = 2k − 1, where sample is ordered from a sample of size n = 2k − 1, where sample is ordered 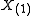 to to 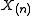 |
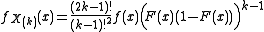 |
| Any distribution with distribution function F | Maximum 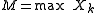 from a random sample of size n from a random sample of size n |
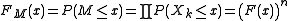 |
Statistical inference
In the theory of statistical inferenceStatistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
, the idea of a sufficient statistic provides the basis of choosing a statistic (as a function of the sample data points) in such a way that no information is lost by replacing the full probabilistic description of the sample with the sampling distribution of the selected statistic.
In frequentist inference
Frequentist inference
Frequentist inference is one of a number of possible ways of formulating generally applicable schemes for making statistical inferences: that is, for drawing conclusions from statistical samples. An alternative name is frequentist statistics...
, for example in the development of a statistical hypothesis test or a confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
, the availability of the sampling distribution of a statistic (or an approximation to this in the form of an asymptotic distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
) can allow the ready formulation of such procedures, whereas the development of procedures starting from the joint distribution of the sample would be less straightforward.
In Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, when the sampling distribution of a statistic is available, one can consider replacing the final outcome of such procedures, specifically the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
s of any unknown quantities given the sample data, by the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
s of any unknown quantities given selected sample statistics. Such a procedure would involve the sampling distribution of the statistics. The results would be identical provided the statistics chosen are jointly sufficient statistics.

