
Standard score
Encyclopedia
In statistics
, a standard score indicates how many standard deviation
s an observation or datum
is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score
and then dividing the difference by the population
standard deviation
. This conversion process is called standardizing or normalizing; however, "normalizing" can refer to many types of ratios; see normalization (statistics)
for more.
Standard scores are also called z-values, z-scores, normal scores, and standardized variables; the use of "Z" is because the normal distribution is also known as the "Z distribution". They are most frequently used to compare a sample to a standard normal deviate
(standard normal distribution, with μ = 0 and σ = 1), though they can be defined without assumptions of normality.
The z-score is only defined if one knows the population parameters, as in standardized testing; if one only has a sample set, then the analogous computation with sample mean and sample standard deviation yields the Student's t-statistic
.
The standard score is not the same as the z-factor
used in the analysis of high-throughput screening
data, but is sometimes confused with it.
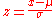
where:
The quantity z represents the distance between the raw score and the population mean in units of the standard deviation. z is negative when the raw score is below the mean, positive when above.
A key point is that calculating z requires the population mean and the population standard deviation, not the sample mean or sample deviation. It requires knowing the population parameters, not the statistics of a sample drawn from the population of interest. But knowing the true standard deviation of a population is often unrealistic except in cases such as standardized testing, where the entire population is measured. In cases where it is impossible to measure every member of a population, the standard deviation may be estimated using a random sample. For example, a population of people who smoke cigarette
s is not fully measured.
in standardized testing – the analog of the Student's t-test
for a population whose parameters are known, rather than estimated. As it is very unusual to know the entire population, the t-test is much more widely used.
and prediction interval
may be determined from the standard score.
With known mean and known variance, prediction intervals can be calculated by subtracting from or adding to the mean (µ) with the standard deviation (σ) multiplied by a standard score (z) that is specific for what prediction intervals are desired:
About 68.27% of the values lie within 1 standard deviation of the mean. Similarly, about 95.45% of the values lie within 2 standard deviations of the mean. Nearly all (99.73%) of the values lie within 3 standard deviations of the mean. This is known as the 68-95-99.7 rule
.
For example, to calculate the 95% prediction interval for a normal distribution with a mean (µ) of 5 and a standard deviation (σ) of 1, then the lower limit of the prediction interval is approximately 5 ‒ (1*2) = 3, and the upper limit is approximately 7, thus giving a prediction interval of approximately 3 to 7.
, a random variable
X is standardized using the theoretical (population) mean and standard deviation:

where is the mean
is the mean
and the standard deviation
the standard deviation
of the probability distribution
of X.
If the random variable under consideration is the sample mean:

then the standardized version is

See normalization (statistics)
for other forms of normalization.
A common name for standard score is the z-score. It is often used in statistics.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a standard score indicates how many standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
s an observation or datum
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score
Raw score
In statistics and data analysis, a raw score is an original datum that has not been transformed. This may include, for example, the original result obtained by a student on a test as opposed to that score after transformation to a standard score or percentile rank or the like.Often the conversion...
and then dividing the difference by the population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
. This conversion process is called standardizing or normalizing; however, "normalizing" can refer to many types of ratios; see normalization (statistics)
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
for more.
Standard scores are also called z-values, z-scores, normal scores, and standardized variables; the use of "Z" is because the normal distribution is also known as the "Z distribution". They are most frequently used to compare a sample to a standard normal deviate
Standard normal deviate
A standard normal deviate is a normally distributed random variable with expected value 0 and variance 1. A fuller term is standard normal random variable...
(standard normal distribution, with μ = 0 and σ = 1), though they can be defined without assumptions of normality.
The z-score is only defined if one knows the population parameters, as in standardized testing; if one only has a sample set, then the analogous computation with sample mean and sample standard deviation yields the Student's t-statistic
Student's t-statistic
In statistics, the t-statistic is a ratio of the departure of an estimated parameter from its notional value and its standard error. It is used in hypothesis testing, for example in the Student's t-test, in the augmented Dickey–Fuller test, and in bootstrapping.-Definition:Let \scriptstyle\hat\beta...
.
The standard score is not the same as the z-factor
Z-factor
The Z-factor is a measure of statistical effect size. It has been proposed for use in high-throughput screening to judge whether the response in a particular assay is large enough to warrant further attention.-Background:...
used in the analysis of high-throughput screening
High-throughput screening
High-throughput screening is a method for scientific experimentation especially used in drug discovery and relevant to the fields of biology and chemistry. Using robotics, data processing and control software, liquid handling devices, and sensitive detectors, High-Throughput Screening allows a...
data, but is sometimes confused with it.
Calculation from raw score
The standard score is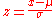
where:
- x is a raw score to be standardized;
- μ is the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the population; - σ is the standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the population.
The quantity z represents the distance between the raw score and the population mean in units of the standard deviation. z is negative when the raw score is below the mean, positive when above.
A key point is that calculating z requires the population mean and the population standard deviation, not the sample mean or sample deviation. It requires knowing the population parameters, not the statistics of a sample drawn from the population of interest. But knowing the true standard deviation of a population is often unrealistic except in cases such as standardized testing, where the entire population is measured. In cases where it is impossible to measure every member of a population, the standard deviation may be estimated using a random sample. For example, a population of people who smoke cigarette
Cigarette
A cigarette is a small roll of finely cut tobacco leaves wrapped in a cylinder of thin paper for smoking. The cigarette is ignited at one end and allowed to smoulder; its smoke is inhaled from the other end, which is held in or to the mouth and in some cases a cigarette holder may be used as well...
s is not fully measured.
Applications
The z-score is most often used in the z-testZ-test
A Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Due to the central limit theorem, many test statistics are approximately normally distributed for large samples...
in standardized testing – the analog of the Student's t-test
Student's t-test
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
for a population whose parameters are known, rather than estimated. As it is very unusual to know the entire population, the t-test is much more widely used.
Percentile ranks and prediction intervals
With a population that is normally distributed with known mean and known variance, the percentile rankPercentile rank
The percentile rank of a score is the percentage of scores in its frequency distribution that are the same or lower than it. For example, a test score that is greater than 75% of the scores of people taking the test is said to be at the 75th percentile....
and prediction interval
Prediction interval
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which future observations will fall, with a certain probability, given what has already been observed...
may be determined from the standard score.
With known mean and known variance, prediction intervals can be calculated by subtracting from or adding to the mean (µ) with the standard deviation (σ) multiplied by a standard score (z) that is specific for what prediction intervals are desired:
| Prediction interval | Standard score (z) |
|---|---|
| 50% | 0.67 |
| 68% | 1.00 |
| 90% | 1.64 |
| 95% | 1.96 |
| 99% | 2.58 |
- Lower limit of prediction interval = µ - σz
- Upper limit of prediction interval = µ + σz
About 68.27% of the values lie within 1 standard deviation of the mean. Similarly, about 95.45% of the values lie within 2 standard deviations of the mean. Nearly all (99.73%) of the values lie within 3 standard deviations of the mean. This is known as the 68-95-99.7 rule
68-95-99.7 rule
In statistics, the 68-95-99.7 rule, or three-sigma rule, or empirical rule, states that for a normal distribution, nearly all values lie within 3 standard deviations of the mean....
.
For example, to calculate the 95% prediction interval for a normal distribution with a mean (µ) of 5 and a standard deviation (σ) of 1, then the lower limit of the prediction interval is approximately 5 ‒ (1*2) = 3, and the upper limit is approximately 7, thus giving a prediction interval of approximately 3 to 7.
Contributions to trend
Z-scores can be used as a way of understanding the contributions from various subsets of data to an overall test of trend, such as trends in the rate of occurrence of cancer and the subsets considered approximately 55 different types of cancer, together with various groupings of these types. In this instance, the use of z-scores is not immediately as a test statistic for a significance test, but rather as a numerical guide to finding subsets of data which might show different trends than others.Standardizing in mathematical statistics
In mathematical statisticsMathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
, a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X is standardized using the theoretical (population) mean and standard deviation:

where
 is the mean
is the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and
 the standard deviation
the standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of X.
If the random variable under consideration is the sample mean:

then the standardized version is

See normalization (statistics)
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
for other forms of normalization.
A common name for standard score is the z-score. It is often used in statistics.
See also
- Central momentCentral momentIn probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
- Moment (mathematics)Moment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
- Normalization (statistics)Normalization (statistics)In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
- Sampling distributionSampling distributionIn statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
- Standard normal deviateStandard normal deviateA standard normal deviate is a normally distributed random variable with expected value 0 and variance 1. A fuller term is standard normal random variable...
- Standard normal tableStandard normal tableA standard normal table also called the "Unit Normal Table" is a mathematical table for the values of Φ, the cumulative distribution function of the normal distribution....
- Student's t-testStudent's t-testA t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
- Student's t-statisticStudent's t-statisticIn statistics, the t-statistic is a ratio of the departure of an estimated parameter from its notional value and its standard error. It is used in hypothesis testing, for example in the Student's t-test, in the augmented Dickey–Fuller test, and in bootstrapping.-Definition:Let \scriptstyle\hat\beta...
- Studentized residualStudentized residualIn statistics, a studentized residual is the quotient resulting from the division of a residual by an estimate of its standard deviation. Typically the standard deviations of residuals in a sample vary greatly from one data point to another even when the errors all have the same standard...
- Z-factorZ-factorThe Z-factor is a measure of statistical effect size. It has been proposed for use in high-throughput screening to judge whether the response in a particular assay is large enough to warrant further attention.-Background:...
- Z-testZ-testA Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Due to the central limit theorem, many test statistics are approximately normally distributed for large samples...
- Sten scoresSten scoresThe results for some scales of some psychometric instruments are returned as sten scores, sten being an abbreviation for 'Standard Ten' and thus closely related to stanine scores.- Definition :...
Further reading
}}- Richard J. Larsen and Morris L. Marx (2000) An Introduction to Mathematical Statistics and Its Applications, Third Edition, ISBN 0139223037. p. 282.

