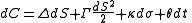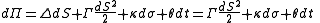Option (finance)
Encyclopedia
In finance
, an option is a derivative
financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the corresponding obligation to fulfill the transaction. The price of an option derives from the difference between the reference price and the value of the underlying
asset (commonly a stock
, a bond
, a currency
or a futures contract
) plus a premium based on the time remaining until the expiration of the option. Other types of options exist, and options can in principle be created for any type of valuable asset.
An option which conveys the right to buy something at a specific price is called a call
; an option which conveys the right to sell something at a specific price is called a put
. The reference price at which the underlying asset may be traded is called the strike price
or exercise price. The process of activating an option and thereby trading the underlying at the agreed-upon price is referred to as exercising
it. Most options have an expiration date
. If the option is not exercised by the expiration date, it becomes void and worthless.
In return for assuming the obligation, called writing the option, the originator of the option collects a payment, the premium, from the buyer. The writer of an option must make good on delivering (or receiving) the underlying asset or its cash equivalent, if the option is exercised.
An option can usually be sold by its original buyer to another party. Many options are created in standardized form and traded on an anonymous options exchange
among the general public, while other over-the-counter
options are customized ad hoc to the desires of the buyer, usually by an investment bank.
. Option contracts may be quite complicated; however, at minimum, they usually contain the following specifications:
s, which are awarded by a company to their employees as a form of incentive compensation. Other types of options exist in many financial contracts, for example real estate option
s are often used to assemble large parcels of land, and prepayment options are usually included in mortgage loan
s. However, many of the valuation and risk management principles apply across all financial options.
pricing and using stochastic calculus
. The most basic model is the Black–Scholes model. More sophisticated models are used to model the volatility smile
. These models are implemented using a variety of numerical techniques.
In general, standard option valuation models depend on the following factors:
More advanced models can require additional factors, such as an estimate of how volatility changes over time and for various underlying price levels, or the dynamics of stochastic interest rates.
The following are some of the principal valuation techniques used in practice to evaluate option contracts.
and later work by Edward O. Thorp
, Fischer Black
and Myron Scholes
made a major breakthrough by deriving a differential equation that must be satisfied by the price of any derivative dependent on a non-dividend-paying stock. By employing the technique of constructing a risk neutral portfolio that replicates the returns of holding an option, Black and Scholes produced a closed-form solution for a European option's theoretical price. At the same time, the model generates hedge parameters
necessary for effective risk management of option holdings. While the ideas behind the Black–Scholes model were ground-breaking and eventually led to Scholes
and Merton
receiving the Swedish Central Bank's associated Prize for Achievement in Economics (a.k.a., the Nobel Prize
in Economics),
the application of the model in actual options trading is clumsy because of the assumptions of continuous (or no) dividend payment, constant volatility, and a constant interest rate. Nevertheless, the Black–Scholes model is still one of the most important methods and foundations for the existing financial market in which the result is within the reasonable range.
for options of lower strike prices are typically higher than for higher strike prices, suggesting that volatility is stochastic, varying both for time and for the price level of the underlying security. Stochastic volatility
models have been developed including one developed by S.L. Heston
. One principal advantage of the Heston model is that it can be solved in closed-form, while other stochastic volatility models require complex numerical methods.
and using analytical methods develop closed form solutions
such as Black–Scholes and the Black model
. The resulting solutions are readily computable, as are their "Greeks"
.
, Stephen Ross
and Mark Rubinstein
developed the original version of the binomial options pricing model
.
It models the dynamics of the option's theoretical value for discrete
time intervals over the option's life. The model starts with a binomial tree of discrete future possible underlying stock prices. By constructing a riskless portfolio of an option and stock (as in the Black–Scholes model) a simple formula can be used to find the option price at each node in the tree. This value can approximate the theoretical value produced by Black Scholes, to the desired degree of precision. However, the binomial model is considered more accurate than Black–Scholes because it is more flexible; e.g., discrete future dividend payments can be modeled correctly at the proper forward time steps, and American options can be modeled as well as European ones. Binomial models are widely used by professional option traders. The Trinomial tree
is a similar model, allowing for an up, down or stable path; although considered more accurate, particularly when fewer time-steps are modelled, it is less commonly used as its implementation is more complex.
Note though, that despite its flexibility, using simulation for American styled options is somewhat more complex than for lattice based models.
s (see for example Black–Scholes PDE). Once expressed in this form, a finite difference model
can be derived, and the valuation obtained. A number of implementations of finite difference methods exist for option valuation, including: explicit finite difference, implicit finite difference and the Crank-Nicholson method. A trinomial tree option pricing model can be shown to be a simplified application of the explicit finite difference method. Although the finite difference approach is mathematically sophisticated, it is particularly useful where changes are assumed over time in model inputs – for example dividend yield, risk free rate, or volatility, or some combination of these – that are not tractable
in closed form.
s. Additionally, various short rate model
s have been developed for the valuation of interest rate derivatives, bond option
s and swaption
s. These, similarly, allow for closed-form, lattice-based, and simulation-based modelling, with corresponding advantages and considerations.
from holding an option varies non-linearly with the value of the underlying and other factors. Therefore, the risks associated with holding options are more complicated to understand and predict.
In general, the change in the value of an option can be derived from Ito's lemma
as:
where the Greeks
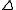 ,
, 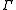 ,
,  and
and 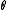 are the standard hedge parameters calculated from an option valuation model, such as Black–Scholes, and
are the standard hedge parameters calculated from an option valuation model, such as Black–Scholes, and 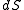 ,
, 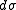 and
and  are unit changes in the underlying's price, the underlying's volatility and time, respectively.
are unit changes in the underlying's price, the underlying's volatility and time, respectively.
Thus, at any point in time, one can estimate the risk inherent in holding an option by calculating its hedge parameters and then estimating the expected change in the model inputs,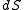 ,
, 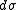 and
and 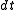 , provided the changes in these values are small. This technique can be used effectively to understand and manage the risks associated with standard options. For instance, by offsetting a holding in an option with the quantity
, provided the changes in these values are small. This technique can be used effectively to understand and manage the risks associated with standard options. For instance, by offsetting a holding in an option with the quantity 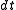 of shares in the underlying, a trader can form a delta neutral
of shares in the underlying, a trader can form a delta neutral
portfolio that is hedged from loss for small changes in the underlying's price. The corresponding price sensitivity formula for this portfolio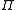 is:
is:
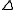 ,
, 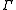 ,
,  ,
, 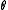 are (0.439, 0.0631, 9.6, and −0.022), respectively. Assume that on the following day, XYZ stock rises to $48.5 and volatility falls to 23.5%. We can calculate the estimated value of the call option by applying the hedge parameters to the new model inputs as:
are (0.439, 0.0631, 9.6, and −0.022), respectively. Assume that on the following day, XYZ stock rises to $48.5 and volatility falls to 23.5%. We can calculate the estimated value of the call option by applying the hedge parameters to the new model inputs as:
Under this scenario, the value of the option increases by $0.0614 to $1.9514, realizing a profit of $6.14. Note that for a delta neutral portfolio, where by the trader had also sold 44 shares of XYZ stock as a hedge, the net loss under the same scenario would be ($15.86).
s.
Listings and prices are tracked and can be looked up by ticker symbol
.
By publishing continuous, live markets for option prices, an exchange enables independent parties to engage in price discovery and execute transactions. As an intermediary to both sides of the transaction, the benefits the exchange provides to the transaction include:
Over-the-counter
options contracts are not traded on exchanges, but instead between two independent parties. Ordinarily, at least one of the counterparties is a well-capitalized institution. By avoiding an exchange, users of OTC options can narrowly tailor the terms of the option contract to suit individual business requirements. In addition, OTC option transactions generally do not need to be advertised to the market and face little or no regulatory requirements. However, OTC counterparties must establish credit lines with each other, and conform to each others clearing and settlement procedures.
With few exceptions, there are no secondary markets for employee stock options. These must either be exercised by the original grantee or allowed to expire worthless.
 A trader who believes that a stock's price will increase might buy the right to purchase the stock (a call option
A trader who believes that a stock's price will increase might buy the right to purchase the stock (a call option
) rather than just purchase the stock itself. He would have no obligation to buy the stock, only the right to do so until the expiration date. If the stock price at expiration is above the exercise price by more than the premium (price) paid, he will profit. If the stock price at expiration is lower than the exercise price, he will let the call contract expire worthless, and only lose the amount of the premium. A trader might buy the option instead of shares, because for the same amount of money, he can control (leverage
) a much larger number of shares.
 A trader who believes that a stock's price will decrease can buy the right to sell the stock at a fixed price (a put option
A trader who believes that a stock's price will decrease can buy the right to sell the stock at a fixed price (a put option
). He will be under no obligation to sell the stock, but has the right to do so until the expiration date. If the stock price at expiration is below the exercise price by more than the premium paid, he will profit. If the stock price at expiration is above the exercise price, he will let the put contract expire worthless and only lose the premium paid.
 A trader who believes that a stock price will decrease can sell the stock short or instead sell, or "write," a call. The trader selling a call has an obligation to sell the stock to the call buyer at the buyer's option. If the stock price decreases, the short call position will make a profit in the amount of the premium. If the stock price increases over the exercise price by more than the amount of the premium, the short will lose money, with the potential loss unlimited.
A trader who believes that a stock price will decrease can sell the stock short or instead sell, or "write," a call. The trader selling a call has an obligation to sell the stock to the call buyer at the buyer's option. If the stock price decreases, the short call position will make a profit in the amount of the premium. If the stock price increases over the exercise price by more than the amount of the premium, the short will lose money, with the potential loss unlimited.
 A trader who believes that a stock price will increase can buy the stock or instead sell, or "write", a put. The trader selling a put has an obligation to buy the stock from the put buyer at the put buyer's option. If the stock price at expiration is above the exercise price, the short put position will make a profit in the amount of the premium. If the stock price at expiration is below the exercise price by more than the amount of the premium, the trader will lose money, with the potential loss being up to the full value of the stock. A benchmark index for the performance of a cash-secured short put option position is the CBOE S&P 500 PutWrite Index (ticker PUT).
A trader who believes that a stock price will increase can buy the stock or instead sell, or "write", a put. The trader selling a put has an obligation to buy the stock from the put buyer at the put buyer's option. If the stock price at expiration is above the exercise price, the short put position will make a profit in the amount of the premium. If the stock price at expiration is below the exercise price by more than the amount of the premium, the trader will lose money, with the potential loss being up to the full value of the stock. A benchmark index for the performance of a cash-secured short put option position is the CBOE S&P 500 PutWrite Index (ticker PUT).


 Combining any of the four basic kinds of option trades (possibly with different exercise prices and maturities) and the two basic kinds of stock trades (long and short) allows a variety of options strategies
Combining any of the four basic kinds of option trades (possibly with different exercise prices and maturities) and the two basic kinds of stock trades (long and short) allows a variety of options strategies
. Simple strategies usually combine only a few trades, while more complicated strategies can combine several.
Strategies are often used to engineer a particular risk profile to movements in the underlying security. For example, buying a butterfly
spread (long one X1 call, short two X2 calls, and long one X3 call) allows a trader to profit if the stock price on the expiration date is near the middle exercise price, X2, and does not expose the trader to a large loss.
An Iron condor
is a strategy that is similar to a butterfly spread, but with different strikes for the short options – offering a larger likelihood of profit but with a lower net credit compared to the butterfly spread.
Selling a straddle
(selling both a put and a call at the same exercise price) would give a trader a greater profit than a butterfly if the final stock price is near the exercise price, but might result in a large loss.
Similar to the straddle is the strangle
which is also constructed by a call and a put, but whose strikes are different, reducing the net debit of the trade, but also reducing the risk of loss in the trade.
One well-known strategy is the covered call
, in which a trader buys a stock (or holds a previously-purchased long stock position), and sells a call. If the stock price rises above the exercise price, the call will be exercised and the trader will get a fixed profit. If the stock price falls, the call will not be exercised, and any loss incurred to the trader will be partially offset by the premium received from selling the call. Overall, the payoffs match the payoffs from selling a put. This relationship is known as put-call parity and offers insights for financial theory. A benchmark index for the performance of a buy-write
strategy is the CBOE S&P 500 BuyWrite Index (ticker symbol BXM).
market, call options have long been used to assemble large parcels of land from separate owners; e.g., a developer pays for the right to buy several adjacent plots, but is not obligated to buy these plots and might not unless he can buy all the plots in the entire parcel. Film or theatrical producers often buy the right — but not the obligation — to dramatize a specific book or script.
Lines of credit
give the potential borrower the right — but not the obligation — to borrow within a specified time period.
Many choices, or embedded options, have traditionally been included in bond
contracts. For example many bonds are convertible
into common stock at the buyer's option, or may be called (bought back) at specified prices at the issuer's option. Mortgage
borrowers have long had the option to repay the loan early, which corresponds to a callable bond option.
In London, puts and "refusals" (calls) first became well-known trading instruments in the 1690s during the reign of William and Mary
.
Privileges were options sold over the counter in nineteenth century America, with both puts and calls on shares offered by specialized dealers. Their exercise price was fixed at a rounded-off market price on the day or week that the option was bought, and the expiry date was generally three months after purchase. They were not traded in secondary markets.
Supposedly the first option buyer in the world was the ancient Greek
mathematician and philosopher Thales
of Miletus. On a certain occasion, it was predicted that the season's olive
harvest would be larger than usual, and during the off-season he acquired the right to use a number of olive presses the following spring. When spring came and the olive harvest was larger than expected he exercised his options and then rented the presses out at much higher price than he paid for his 'option'.
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, an option is a derivative
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the corresponding obligation to fulfill the transaction. The price of an option derives from the difference between the reference price and the value of the underlying
Underlying
In finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
asset (commonly a stock
Stock
The capital stock of a business entity represents the original capital paid into or invested in the business by its founders. It serves as a security for the creditors of a business since it cannot be withdrawn to the detriment of the creditors...
, a bond
Bond (finance)
In finance, a bond is a debt security, in which the authorized issuer owes the holders a debt and, depending on the terms of the bond, is obliged to pay interest to use and/or to repay the principal at a later date, termed maturity...
, a currency
Currency
In economics, currency refers to a generally accepted medium of exchange. These are usually the coins and banknotes of a particular government, which comprise the physical aspects of a nation's money supply...
or a futures contract
Futures contract
In finance, a futures contract is a standardized contract between two parties to exchange a specified asset of standardized quantity and quality for a price agreed today with delivery occurring at a specified future date, the delivery date. The contracts are traded on a futures exchange...
) plus a premium based on the time remaining until the expiration of the option. Other types of options exist, and options can in principle be created for any type of valuable asset.
An option which conveys the right to buy something at a specific price is called a call
Call option
A call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller...
; an option which conveys the right to sell something at a specific price is called a put
Put option
A put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
. The reference price at which the underlying asset may be traded is called the strike price
Strike price
In options, the strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the spot price of the underlying instrument at that time.Formally, the strike...
or exercise price. The process of activating an option and thereby trading the underlying at the agreed-upon price is referred to as exercising
Exercise (options)
The owner of an option contract may exercise it, indicating that the financial transaction specified by the contract is to be enacted immediately between the two parties, and the contract itself is terminated...
it. Most options have an expiration date
Expiration (options)
For an option contract, expiration is the date on which the contract expires. The option holder must elect to exercise the option or allow it to expire worthless.Typically, option contracts expire according to a pre-determined calendar. For instance, for U.S...
. If the option is not exercised by the expiration date, it becomes void and worthless.
In return for assuming the obligation, called writing the option, the originator of the option collects a payment, the premium, from the buyer. The writer of an option must make good on delivering (or receiving) the underlying asset or its cash equivalent, if the option is exercised.
An option can usually be sold by its original buyer to another party. Many options are created in standardized form and traded on an anonymous options exchange
Exchange (organized market)
An exchange is a highly organized market where tradable securities, commodities, foreign exchange, futures, and options contracts are sold and bought.-Description:...
among the general public, while other over-the-counter
Over-the-counter (finance)
Within the derivatives markets, many products are traded through exchanges. An exchange has the benefit of facilitating liquidity and also mitigates all credit risk concerning the default of a member of the exchange. Products traded on the exchange must be well standardised to transparent trading....
options are customized ad hoc to the desires of the buyer, usually by an investment bank.
Contract specifications
Every financial option is a contract between the two counterparties with the terms of the option specified in a term sheetTerm sheet
A term sheet is a bullet-point document outlining the material terms and conditions of a business agreement. After a term sheet has been "executed", it guides legal counsel in the preparation of a proposed "final agreement"...
. Option contracts may be quite complicated; however, at minimum, they usually contain the following specifications:
- whether the option holder has the right to buy (a call optionCall optionA call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller...
) or the right to sell (a put optionPut optionA put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
) - the quantity and class of the underlyingUnderlyingIn finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
asset(s) (e.g., 100 shares of XYZ Co. B stock) - the strike priceStrike priceIn options, the strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the spot price of the underlying instrument at that time.Formally, the strike...
, also known as the exercise price, which is the price at which the underlying transaction will occur upon exerciseExercise (options)The owner of an option contract may exercise it, indicating that the financial transaction specified by the contract is to be enacted immediately between the two parties, and the contract itself is terminated... - the expirationExpiration (options)For an option contract, expiration is the date on which the contract expires. The option holder must elect to exercise the option or allow it to expire worthless.Typically, option contracts expire according to a pre-determined calendar. For instance, for U.S...
date, or expiry, which is the last date the option can be exercised - the settlement termsSettlement (finance)Settlement of securities is a business process whereby securities or interests in securities are delivered, usually against payment of money, to fulfill contractual obligations, such as those arising under securities trades....
, for instance whether the writer must deliver the actual asset on exercise, or may simply tender the equivalent cash amount - the terms by which the option is quoted in the market to convert the quoted price into the actual premium – the total amount paid by the holder to the writer
Exchange-traded options
- Exchange-traded options (also called "listed options") are a class of exchange-traded derivatives. Exchange traded options have standardized contracts, and are settled through a clearing houseClearing house (finance)A clearing house is a financial institution that provides clearing and settlement services for financial and commodities derivatives and securities transactions...
with fulfillment guaranteed by the credit of the exchange. Since the contracts are standardized, accurate pricing models are often available. Exchange-traded options include:- stock options,
- commodity options,
- bond optionBond optionIn finance, a bond option is an option to buy or sell a bond at a certain price on or before the option expiry date. These instruments are typically traded OTC....
s and other interest rate optionsInterest rate derivativeAn interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate... - stock market index optionStock market index optionStock market index option is a type of option, which is a financial derivative. Index options may be tied to the price of either broad-based indexes like the S&P 500 Index or the Russell 3000 Index or to narrow-based indexes, which is an index that is limited to a particular industry like the...
s or, simply, index options and - options on futures contracts
- callable bull/bear contractCallable bull/bear contractA callable bull/bear contract, or CBBC in short form, is a derivative that provides investors with a leveraged investment in underlying assets, which can be a single stock, or an index. They are usually issued by third parties, mostly investment banks, but neither stock exchanges nor asset owners...
Over-the-counter
- Over-the-counterOver-the-counter (finance)Within the derivatives markets, many products are traded through exchanges. An exchange has the benefit of facilitating liquidity and also mitigates all credit risk concerning the default of a member of the exchange. Products traded on the exchange must be well standardised to transparent trading....
options (OTC options, also called "dealer options") are traded between two private parties, and are not listed on an exchange. The terms of an OTC option are unrestricted and may be individually tailored to meet any business need. In general, at least one of the counterparties to an OTC option is a well-capitalized institution. Option types commonly traded over the counter include:
- interest rate options
- currency cross rate options, and
- options on swapSwap (finance)In finance, a swap is a derivative in which counterparties exchange certain benefits of one party's financial instrument for those of the other party's financial instrument. The benefits in question depend on the type of financial instruments involved...
s or swaptionSwaptionA swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps....
s.
Other option types
Another important class of options, particularly in the U.S., are employee stock optionEmployee stock option
An employee stock option is a call option on the common stock of a company, issued as a form of non-cash compensation. Restrictions on the option attempt to align the holder's interest with those of the business shareholders. If the company's stock rises, holders of options generally experience a...
s, which are awarded by a company to their employees as a form of incentive compensation. Other types of options exist in many financial contracts, for example real estate option
Option (law)
In law, an option is the right to convey a piece of property. The person granting the option is called the optionor and the person who has the benefit of the option is called the optionee .Options characteristically exist in one of two forms:* Call options, which give the beneficiary the right to...
s are often used to assemble large parcels of land, and prepayment options are usually included in mortgage loan
Mortgage loan
A mortgage loan is a loan secured by real property through the use of a mortgage note which evidences the existence of the loan and the encumbrance of that realty through the granting of a mortgage which secures the loan...
s. However, many of the valuation and risk management principles apply across all financial options.
Option styles
Naming conventions are used to help identify properties common to many different types of options. These include:- European option – an option that may only be exercisedExercise (options)The owner of an option contract may exercise it, indicating that the financial transaction specified by the contract is to be enacted immediately between the two parties, and the contract itself is terminated...
on expirationExpiration (options)For an option contract, expiration is the date on which the contract expires. The option holder must elect to exercise the option or allow it to expire worthless.Typically, option contracts expire according to a pre-determined calendar. For instance, for U.S...
. - American option – an option that may be exercised on any trading day on or before expiry.
- Bermudan option – an option that may be exercised only on specified dates on or before expiration.
- Barrier option – any option with the general characteristic that the underlying security's price must pass a certain level or "barrier" before it can be exercised.
- Exotic option – any of a broad category of options that may include complex financial structures.
- Vanilla option – any option that is not exotic.
Valuation models
The value of an option can be estimated using a variety of quantitative techniques based on the concept of risk neutralRisk neutral
In economics and finance, risk neutral behavior is between risk aversion and risk seeking. If offered either €50 or a 50% chance of each of €100 and nothing, a risk neutral person would have no preference between the two options...
pricing and using stochastic calculus
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
. The most basic model is the Black–Scholes model. More sophisticated models are used to model the volatility smile
Volatility Smile
In finance, the volatility smile is a long-observed pattern in which at-the-money options tend to have lower implied volatilities than in- or out-of-the-money options. The pattern displays different characteristics for different markets and results from the probability of extreme moves...
. These models are implemented using a variety of numerical techniques.
In general, standard option valuation models depend on the following factors:
- The current market price of the underlying security,
- the strike priceStrike priceIn options, the strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the spot price of the underlying instrument at that time.Formally, the strike...
of the option, particularly in relation to the current market price of the underlying (in the money vs. out of the money), - the cost of holding a position in the underlying security, including interest and dividends,
- the time to expirationExpiration (options)For an option contract, expiration is the date on which the contract expires. The option holder must elect to exercise the option or allow it to expire worthless.Typically, option contracts expire according to a pre-determined calendar. For instance, for U.S...
together with any restrictions on when exercise may occur, and - an estimate of the future volatilityVolatility (finance)In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
of the underlying security's price over the life of the option.
More advanced models can require additional factors, such as an estimate of how volatility changes over time and for various underlying price levels, or the dynamics of stochastic interest rates.
The following are some of the principal valuation techniques used in practice to evaluate option contracts.
Black–Scholes
Following early work by Louis BachelierLouis Bachelier
-External links:** Louis Bachelier webpage at the Université de Franche-Comté, Besançon / France. Text in French.** also from Index Funds Advisors, this discussion of...
and later work by Edward O. Thorp
Edward O. Thorp
Edward Oakley Thorp is an American mathematics professor, author, hedge fund manager, and blackjack player. He was a pioneer in modern applications of probability theory, including the harnessing of very small correlations for reliable financial gain.He was the author of Beat the Dealer, the first...
, Fischer Black
Fischer Black
Fischer Sheffey Black was an American economist, best known as one of the authors of the famous Black–Scholes equation.-Background:...
and Myron Scholes
Myron Scholes
Myron Samuel Scholes is a Canadian-born American financial economist who is best known as one of the authors of the Black–Scholes equation. In 1997 he was awarded the Nobel Memorial Prize in Economic Sciences for a method to determine the value of derivatives...
made a major breakthrough by deriving a differential equation that must be satisfied by the price of any derivative dependent on a non-dividend-paying stock. By employing the technique of constructing a risk neutral portfolio that replicates the returns of holding an option, Black and Scholes produced a closed-form solution for a European option's theoretical price. At the same time, the model generates hedge parameters
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivities of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of...
necessary for effective risk management of option holdings. While the ideas behind the Black–Scholes model were ground-breaking and eventually led to Scholes
Myron Scholes
Myron Samuel Scholes is a Canadian-born American financial economist who is best known as one of the authors of the Black–Scholes equation. In 1997 he was awarded the Nobel Memorial Prize in Economic Sciences for a method to determine the value of derivatives...
and Merton
Robert C. Merton
Robert Carhart Merton is an American economist, Nobel laureate in Economics, and professor at the MIT Sloan School of Management.-Biography:...
receiving the Swedish Central Bank's associated Prize for Achievement in Economics (a.k.a., the Nobel Prize
Nobel Prize
The Nobel Prizes are annual international awards bestowed by Scandinavian committees in recognition of cultural and scientific advances. The will of the Swedish chemist Alfred Nobel, the inventor of dynamite, established the prizes in 1895...
in Economics),
the application of the model in actual options trading is clumsy because of the assumptions of continuous (or no) dividend payment, constant volatility, and a constant interest rate. Nevertheless, the Black–Scholes model is still one of the most important methods and foundations for the existing financial market in which the result is within the reasonable range.
Stochastic volatility models
Since the market crash of 1987, it has been observed that market implied volatilityImplied volatility
In financial mathematics, the implied volatility of an option contract is the volatility of the price of the underlying security that is implied by the market price of the option based on an option pricing model. In other words, it is the volatility that, when used in a particular pricing model,...
for options of lower strike prices are typically higher than for higher strike prices, suggesting that volatility is stochastic, varying both for time and for the price level of the underlying security. Stochastic volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
models have been developed including one developed by S.L. Heston
Heston model
In finance, the Heston model, named after Steven Heston, is a mathematical model describing the evolution of the volatility of an underlying asset...
. One principal advantage of the Heston model is that it can be solved in closed-form, while other stochastic volatility models require complex numerical methods.
Model implementation
Once a valuation model has been chosen, there are a number of different techniques used to take the mathematical models to implement the models.Analytic techniques
In some cases, one can take the mathematical modelMathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
and using analytical methods develop closed form solutions
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
such as Black–Scholes and the Black model
Black model
The Black model is a variant of the Black–Scholes option pricing model. Its primary applications are for pricing bond options, interest rate caps / floors, and swaptions...
. The resulting solutions are readily computable, as are their "Greeks"
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivities of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of...
.
Binomial tree pricing model
Closely following the derivation of Black and Scholes, John CoxJohn C. Cox
John Carrington Cox is the Nomura Professor of Finance at the MIT Sloan School of Management. He is one of the world's leading experts on options theory and one of the inventors of the Cox–Ross–Rubinstein model for option pricing, as well as of the Cox–Ingersoll–Ross model for interest rate dynamics...
, Stephen Ross
Stephen Ross (economist)
Stephen Alan "Steve" Ross is the inaugural Franco Modigliani Professor of Financial Economics at the MIT Sloan School of Management. He is known for initiating several important theories and models in financial economics...
and Mark Rubinstein
Mark Rubinstein
Mark Edward Rubinstein is a leading financial economist and financial engineer. He is currently Professor of Finance at the Haas School of Business of the University of California, Berkeley, where he is involved in teaching courses in the , an academic program that is focused on equipping...
developed the original version of the binomial options pricing model
Binomial options pricing model
In finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
.
It models the dynamics of the option's theoretical value for discrete
Discrete
Discrete in science is the opposite of continuous: something that is separate; distinct; individual.Discrete may refer to:*Discrete particle or quantum in physics, for example in quantum theory...
time intervals over the option's life. The model starts with a binomial tree of discrete future possible underlying stock prices. By constructing a riskless portfolio of an option and stock (as in the Black–Scholes model) a simple formula can be used to find the option price at each node in the tree. This value can approximate the theoretical value produced by Black Scholes, to the desired degree of precision. However, the binomial model is considered more accurate than Black–Scholes because it is more flexible; e.g., discrete future dividend payments can be modeled correctly at the proper forward time steps, and American options can be modeled as well as European ones. Binomial models are widely used by professional option traders. The Trinomial tree
Trinomial Tree
The Trinomial tree is a lattice based computational model used in financial mathematics to price options. It was developed by Phelim Boyle in 1986. It is an extension of the Binomial options pricing model, and is conceptually similar...
is a similar model, allowing for an up, down or stable path; although considered more accurate, particularly when fewer time-steps are modelled, it is less commonly used as its implementation is more complex.
Monte Carlo models
For many classes of options, traditional valuation techniques are intractable because of the complexity of the instrument. In these cases, a Monte Carlo approach may often be useful. Rather than attempt to solve the differential equations of motion that describe the option's value in relation to the underlying security's price, a Monte Carlo model uses simulation to generate random price paths of the underlying asset, each of which results in a payoff for the option. The average of these payoffs can be discounted to yield an expectation value for the option.Note though, that despite its flexibility, using simulation for American styled options is somewhat more complex than for lattice based models.
Finite difference models
The equations used to model the option are often expressed as partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (see for example Black–Scholes PDE). Once expressed in this form, a finite difference model
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
can be derived, and the valuation obtained. A number of implementations of finite difference methods exist for option valuation, including: explicit finite difference, implicit finite difference and the Crank-Nicholson method. A trinomial tree option pricing model can be shown to be a simplified application of the explicit finite difference method. Although the finite difference approach is mathematically sophisticated, it is particularly useful where changes are assumed over time in model inputs – for example dividend yield, risk free rate, or volatility, or some combination of these – that are not tractable
Tractable
Tractable may refer to:*Operation Tractable, a military operation in Normandy 1944*Tractability concerning how easily something can be done...
in closed form.
Other models
Other numerical implementations which have been used to value options include finite element methodFinite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
s. Additionally, various short rate model
Short rate model
In the context of interest rate derivatives, a short-rate model is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,.-The short rate:...
s have been developed for the valuation of interest rate derivatives, bond option
Bond option
In finance, a bond option is an option to buy or sell a bond at a certain price on or before the option expiry date. These instruments are typically traded OTC....
s and swaption
Swaption
A swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps....
s. These, similarly, allow for closed-form, lattice-based, and simulation-based modelling, with corresponding advantages and considerations.
Risks
As with all securities, trading options entails the risk of the option's value changing over time. However, unlike traditional securities, the returnStock option return
Stock option return calculations provide investors an easy metric for comparing stock option positions. For example, for two stock option positions which appear identical, the potential stock option return may be useful for determining which position has the highest relative potential...
from holding an option varies non-linearly with the value of the underlying and other factors. Therefore, the risks associated with holding options are more complicated to understand and predict.
In general, the change in the value of an option can be derived from Ito's lemma
Ito's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
as:
where the Greeks
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivities of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of...
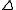 ,
, 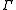 ,
,  and
and 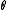 are the standard hedge parameters calculated from an option valuation model, such as Black–Scholes, and
are the standard hedge parameters calculated from an option valuation model, such as Black–Scholes, and 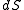 ,
, 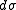 and
and  are unit changes in the underlying's price, the underlying's volatility and time, respectively.
are unit changes in the underlying's price, the underlying's volatility and time, respectively.Thus, at any point in time, one can estimate the risk inherent in holding an option by calculating its hedge parameters and then estimating the expected change in the model inputs,
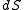 ,
, 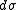 and
and 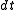 , provided the changes in these values are small. This technique can be used effectively to understand and manage the risks associated with standard options. For instance, by offsetting a holding in an option with the quantity
, provided the changes in these values are small. This technique can be used effectively to understand and manage the risks associated with standard options. For instance, by offsetting a holding in an option with the quantity 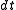 of shares in the underlying, a trader can form a delta neutral
of shares in the underlying, a trader can form a delta neutralDelta neutral
In finance, delta neutral describes a portfolio of related financial securities, in which the portfolio value remains unchanged due to small changes in the value of the underlying security...
portfolio that is hedged from loss for small changes in the underlying's price. The corresponding price sensitivity formula for this portfolio
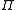 is:
is:Example
A call option expiring in 99 days on 100 shares of XYZ stock is struck at $50, with XYZ currently trading at $48. With future realized volatility over the life of the option estimated at 25%, the theoretical value of the option is $1.89. The hedge parameters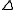 ,
, 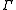 ,
,  ,
, 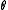 are (0.439, 0.0631, 9.6, and −0.022), respectively. Assume that on the following day, XYZ stock rises to $48.5 and volatility falls to 23.5%. We can calculate the estimated value of the call option by applying the hedge parameters to the new model inputs as:
are (0.439, 0.0631, 9.6, and −0.022), respectively. Assume that on the following day, XYZ stock rises to $48.5 and volatility falls to 23.5%. We can calculate the estimated value of the call option by applying the hedge parameters to the new model inputs as:
Under this scenario, the value of the option increases by $0.0614 to $1.9514, realizing a profit of $6.14. Note that for a delta neutral portfolio, where by the trader had also sold 44 shares of XYZ stock as a hedge, the net loss under the same scenario would be ($15.86).
Pin risk
A special situation called pin risk can arise when the underlying closes at or very close to the option's strike value on the last day the option is traded prior to expiration. The option writer (seller) may not know with certainty whether or not the option will actually be exercised or be allowed to expire worthless. Therefore, the option writer may end up with a large, unwanted residual position in the underlying when the markets open on the next trading day after expiration, regardless of their best efforts to avoid such a residual.Counterparty risk
A further, often ignored, risk in derivatives such as options is counterparty risk. In an option contract this risk is that the seller won't sell or buy the underlying asset as agreed. The risk can be minimized by using a financially strong intermediary able to make good on the trade, but in a major panic or crash the number of defaults can overwhelm even the strongest intermediaries.Trading
The most common way to trade options is via standardized options contracts that are listed by various futures and options exchangeFutures exchange
A futures exchange or futures market is a central financial exchange where people can trade standardized futures contracts; that is, a contract to buy specific quantities of a commodity or financial instrument at a specified price with delivery set at a specified time in the future. These types of...
s.
Listings and prices are tracked and can be looked up by ticker symbol
Option symbol
An option symbol is a code by which options are identified on a futures exchange.-:This article is obsolete, as of February 12th, 2010 when the five-character ticker format described in this article stopped being used in the US and Canada.New standard is now fully in place, as in the first few...
.
By publishing continuous, live markets for option prices, an exchange enables independent parties to engage in price discovery and execute transactions. As an intermediary to both sides of the transaction, the benefits the exchange provides to the transaction include:
- fulfillment of the contract is backed by the credit of the exchange, which typically has the highest rating (AAA),
- counterparties remain anonymous,
- enforcement of market regulation to ensure fairness and transparency, and
- maintenance of orderly markets, especially during fast trading conditions.
Over-the-counter
Over-the-counter (finance)
Within the derivatives markets, many products are traded through exchanges. An exchange has the benefit of facilitating liquidity and also mitigates all credit risk concerning the default of a member of the exchange. Products traded on the exchange must be well standardised to transparent trading....
options contracts are not traded on exchanges, but instead between two independent parties. Ordinarily, at least one of the counterparties is a well-capitalized institution. By avoiding an exchange, users of OTC options can narrowly tailor the terms of the option contract to suit individual business requirements. In addition, OTC option transactions generally do not need to be advertised to the market and face little or no regulatory requirements. However, OTC counterparties must establish credit lines with each other, and conform to each others clearing and settlement procedures.
With few exceptions, there are no secondary markets for employee stock options. These must either be exercised by the original grantee or allowed to expire worthless.
The basic trades of traded stock options (American style)
These trades are described from the point of view of a speculator. If they are combined with other positions, they can also be used in hedging. An option contract in US markets usually represents 100 shares of the underlying security.Long call

Call option
A call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller...
) rather than just purchase the stock itself. He would have no obligation to buy the stock, only the right to do so until the expiration date. If the stock price at expiration is above the exercise price by more than the premium (price) paid, he will profit. If the stock price at expiration is lower than the exercise price, he will let the call contract expire worthless, and only lose the amount of the premium. A trader might buy the option instead of shares, because for the same amount of money, he can control (leverage
Leverage (finance)
In finance, leverage is a general term for any technique to multiply gains and losses. Common ways to attain leverage are borrowing money, buying fixed assets and using derivatives. Important examples are:* A public corporation may leverage its equity by borrowing money...
) a much larger number of shares.
Long put

Put option
A put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
). He will be under no obligation to sell the stock, but has the right to do so until the expiration date. If the stock price at expiration is below the exercise price by more than the premium paid, he will profit. If the stock price at expiration is above the exercise price, he will let the put contract expire worthless and only lose the premium paid.
Short call

Short put

Option strategies



Options strategies
Options strategies can favor movements in the underlying that are bullish, bearish or neutral. In the case of neutral strategies, they can be further classified into those that are bullish on volatility and those that are bearish on volatility...
. Simple strategies usually combine only a few trades, while more complicated strategies can combine several.
Strategies are often used to engineer a particular risk profile to movements in the underlying security. For example, buying a butterfly
Butterfly (options)
In finance, a butterfly is a limited risk, non-directional options strategy that is designed to have a large probability of earning a small limited profit when the future volatility of the underlying is expected to be different from the implied volatility....
spread (long one X1 call, short two X2 calls, and long one X3 call) allows a trader to profit if the stock price on the expiration date is near the middle exercise price, X2, and does not expose the trader to a large loss.
An Iron condor
Iron condor
The iron condor is an advanced option trading strategy utilising two vertical spreads – a put spread and a call spread with the same expiration and four different strikes. If the outer strikes are bought and the inner strikes sold a long iron condor is produced. The converse produces a short iron...
is a strategy that is similar to a butterfly spread, but with different strikes for the short options – offering a larger likelihood of profit but with a lower net credit compared to the butterfly spread.
Selling a straddle
Straddle
In finance, a straddle is an investment strategy involving the purchase or sale of particular option derivatives that allows the holder to profit based on how much the price of the underlying security moves, regardless of the direction of price movement...
(selling both a put and a call at the same exercise price) would give a trader a greater profit than a butterfly if the final stock price is near the exercise price, but might result in a large loss.
Similar to the straddle is the strangle
Strangle (options)
In finance, a strangle is an investment strategy involving the purchase or sale of particular option derivatives that allows the holder to profit based on how much the price of the underlying security moves, with relatively minimal exposure to the direction of price movement...
which is also constructed by a call and a put, but whose strikes are different, reducing the net debit of the trade, but also reducing the risk of loss in the trade.
One well-known strategy is the covered call
Covered call
A covered call is a financial market transaction in which the seller of call options owns the corresponding amount of the underlying instrument, such as shares of a stock or other securities. If a trader buys the underlying instrument at the same time as he sells the call, the strategy is often...
, in which a trader buys a stock (or holds a previously-purchased long stock position), and sells a call. If the stock price rises above the exercise price, the call will be exercised and the trader will get a fixed profit. If the stock price falls, the call will not be exercised, and any loss incurred to the trader will be partially offset by the premium received from selling the call. Overall, the payoffs match the payoffs from selling a put. This relationship is known as put-call parity and offers insights for financial theory. A benchmark index for the performance of a buy-write
Buy-write
The term buy-write is used to describe an investment strategy in which the investor buys stocks and writes call options against the stock position...
strategy is the CBOE S&P 500 BuyWrite Index (ticker symbol BXM).
Historical uses of options
Contracts similar to options are believed to have been used since ancient times. In the real estateReal estate
In general use, esp. North American, 'real estate' is taken to mean "Property consisting of land and the buildings on it, along with its natural resources such as crops, minerals, or water; immovable property of this nature; an interest vested in this; an item of real property; buildings or...
market, call options have long been used to assemble large parcels of land from separate owners; e.g., a developer pays for the right to buy several adjacent plots, but is not obligated to buy these plots and might not unless he can buy all the plots in the entire parcel. Film or theatrical producers often buy the right — but not the obligation — to dramatize a specific book or script.
Lines of credit
Line of credit
A line of credit is any credit source extended to a government, business or individual by a bank or other financial institution. A line of credit may take several forms, such as overdraft protection, demand loan, special purpose, export packing credit, term loan, discounting, purchase of...
give the potential borrower the right — but not the obligation — to borrow within a specified time period.
Many choices, or embedded options, have traditionally been included in bond
Bond (finance)
In finance, a bond is a debt security, in which the authorized issuer owes the holders a debt and, depending on the terms of the bond, is obliged to pay interest to use and/or to repay the principal at a later date, termed maturity...
contracts. For example many bonds are convertible
Convertible bond
In finance, a convertible note is a type of bond that the holder can convert into shares of common stock in the issuing company or cash of equal value, at an agreed-upon price. It is a hybrid security with debt- and equity-like features...
into common stock at the buyer's option, or may be called (bought back) at specified prices at the issuer's option. Mortgage
Mortgage loan
A mortgage loan is a loan secured by real property through the use of a mortgage note which evidences the existence of the loan and the encumbrance of that realty through the granting of a mortgage which secures the loan...
borrowers have long had the option to repay the loan early, which corresponds to a callable bond option.
In London, puts and "refusals" (calls) first became well-known trading instruments in the 1690s during the reign of William and Mary
William and Mary
The phrase William and Mary usually refers to the coregency over the Kingdoms of England, Scotland and Ireland, of King William III & II and Queen Mary II...
.
Privileges were options sold over the counter in nineteenth century America, with both puts and calls on shares offered by specialized dealers. Their exercise price was fixed at a rounded-off market price on the day or week that the option was bought, and the expiry date was generally three months after purchase. They were not traded in secondary markets.
Supposedly the first option buyer in the world was the ancient Greek
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
mathematician and philosopher Thales
Thales
Thales of Miletus was a pre-Socratic Greek philosopher from Miletus in Asia Minor, and one of the Seven Sages of Greece. Many, most notably Aristotle, regard him as the first philosopher in the Greek tradition...
of Miletus. On a certain occasion, it was predicted that the season's olive
Olive
The olive , Olea europaea), is a species of a small tree in the family Oleaceae, native to the coastal areas of the eastern Mediterranean Basin as well as northern Iran at the south end of the Caspian Sea.Its fruit, also called the olive, is of major agricultural importance in the...
harvest would be larger than usual, and during the off-season he acquired the right to use a number of olive presses the following spring. When spring came and the olive harvest was larger than expected he exercised his options and then rented the presses out at much higher price than he paid for his 'option'.
See also
- American Stock ExchangeAmerican Stock ExchangeNYSE Amex Equities, formerly known as the American Stock Exchange is an American stock exchange situated in New York. AMEX was a mutual organization, owned by its members. Until 1953, it was known as the New York Curb Exchange. On January 17, 2008, NYSE Euronext announced it would acquire the...
- Chicago Board Options ExchangeChicago Board Options ExchangeThe Chicago Board Options Exchange , located at 400 South LaSalle Street in Chicago, is the largest U.S. options exchange with annual trading volume that hovered around one billion contracts at the end of 2007...
- EurexEurexEurex is one of the world's leading derivatives exchanges, providing European benchmark derivatives featuring open and low-cost electronic access globally...
- Euronext.liffe
- International Securities ExchangeInternational Securities ExchangeInternational Securities Exchange Holdings, Inc. is a wholly owned subsidiary of German derivatives exchange Eurex. It is a member of the Options Clearing Corporation and the Options Industry Council . Historically, responsibility for organizing the Options Industry Conference is rotated amongst...
- NYSE ArcaNYSE ArcaNYSE Arca, previously known as ArcaEx, an abbreviation of Archipelago Exchange, is a securities exchange on which both stocks and options are traded...
- Philadelphia Stock ExchangePhiladelphia Stock ExchangePhiladelphia Stock Exchange , now known as NASDAQ OMX PHLX, is the oldest stock exchange in the United States, founded in 1790. It is now owned by NASDAQ OMX and located at 1900 Market Street, in Center City Philadelphia.-History:...
- LEAPS (finance)
- Real options analysisReal options analysisReal options valuation, also often termed Real options analysis, applies option valuation techniques to capital budgeting decisions. A real option itself, is the right — but not the obligation — to undertake some business decision; typically the option to make, abandon, expand, or contract a...
- PnL ExplainedPnL ExplainedPnL Explained also called P&L Explain, P&L Attribution or Profit and Loss Explained is a type of report commonly used by traders, especially derivatives traders, that attributes or explains the daily fluctuation in the value of a portfolio of trades to the root causes of the changes.P&L is the...
Further reading
- Fischer Black and Myron S. Scholes. "The Pricing of Options and Corporate Liabilities," Journal of Political Economy, 81 (3), 637–654 (1973).
- Feldman, Barry and Dhuv Roy. "Passive Options-Based Investment Strategies: The Case of the CBOE S&P 500 BuyWrite Index." The Journal of Investing, (Summer 2005).
- Kleinert, HagenHagen KleinertHagen Kleinert is Professor of Theoretical Physics at the Free University of Berlin, Germany , at theWest University of Timişoara, at thein Bishkek. He is also of the...
, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2004); Paperback ISBN 981-238-107-4 (also available online: PDF-files) - Hill, Joanne, Venkatesh Balasubramanian, Krag (Buzz) Gregory, and Ingrid Tierens. "Finding Alpha via Covered Index Writing." Financial Analysts Journal. (Sept.-Oct. 2006). pp. 29–46.
- Moran, Matthew. “Risk-adjusted Performance for Derivatives-based Indexes – Tools to Help Stabilize Returns.” The Journal of Indexes. (Fourth Quarter, 2002) pp. 34 – 40.
- Reilly, Frank and Keith C. Brown, Investment Analysis and Portfolio Management, 7th edition, Thompson Southwestern, 2003, pp. 994–5.
- Schneeweis, Thomas, and Richard Spurgin. "The Benefits of Index Option-Based Strategies for Institutional Portfolios" The Journal of Alternative Investments, (Spring 2001), pp. 44 – 52.
- Whaley, Robert. "Risk and Return of the CBOE BuyWrite Monthly Index" The Journal of Derivatives, (Winter 2002), pp. 35 – 42.
- Bloss, Michael; Ernst, Dietmar; Häcker Joachim (2008): Derivatives – An authoritative guide to derivatives for financial intermediaries and investors Oldenbourg Verlag München ISBN 978-3-486-58632-9
- Espen Gaarder Haug & Nassim Nicholas Taleb (2008): "Why We Have Never Used the Black–Scholes–Merton Option Pricing Formula"