Short rate model
Encyclopedia
In the context of interest rate derivatives, a short-rate model is a mathematical model
that describes the future evolution of interest rate
s by describing the future evolution of the short rate, usually written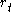
.
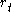, is the (annualized) interest rate at which an entity can borrow money for an infinitesimally short period of time from time t. Specifying the current short rate does not specify the entire yield curve
. However no-arbitrage arguments
show that, under some fairly relaxed technical conditions, if we model the evolution of
as a stochastic process
under a risk-neutral measure
Q then the price at time t of a zero-coupon bond maturing at time T is given by
where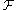
is the natural filtration
for the process. Thus specifying a model for the short rate specifies future bond prices. This means that instantaneous forward rates are also specified by the usual formula
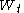represents a standard Brownian motion
under a risk-neutral
probability measure and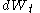
its differential
. Other than Rendleman–Bartter and Ho–Lee, which do not capture the mean reversion
of interest rates, these models can be thought of as specific cases of Ornstein–Uhlenbeck processes. Where the model is lognormal, a variable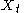
, is assumed to follow an Ornstein–Uhlenbeck process and 
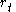is assumed to follow 
. Ho-Lee and subsequent models can be calibrated to market data, meaning that these can exactly return the price of bonds comprising the yield curve.
and Schwartz
two factor model and the Chen three factor model (also called "stochastic mean and stochastic volatility model"):
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
that describes the future evolution of interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
s by describing the future evolution of the short rate, usually written
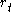.The short rate
The short rate,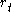, is the (annualized) interest rate at which an entity can borrow money for an infinitesimally short period of time from time t. Specifying the current short rate does not specify the entire yield curveYield curve
In finance, the yield curve is the relation between the interest rate and the time to maturity, known as the "term", of the debt for a given borrower in a given currency. For example, the U.S. dollar interest rates paid on U.S...
. However no-arbitrage arguments
Arbitrage
In economics and finance, arbitrage is the practice of taking advantage of a price difference between two or more markets: striking a combination of matching deals that capitalize upon the imbalance, the profit being the difference between the market prices...
show that, under some fairly relaxed technical conditions, if we model the evolution of
as a stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
under a risk-neutral measure
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
Q then the price at time t of a zero-coupon bond maturing at time T is given by
where
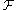is the natural filtrationNatural filtration
In the theory of stochastic processes in mathematics and statistics, the natural filtration associated to a stochastic process is a filtration associated to the process which records its "past behaviour" at each time...
for the process. Thus specifying a model for the short rate specifies future bond prices. This means that instantaneous forward rates are also specified by the usual formula
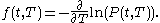
Particular short-rate models
Throughout this section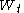 represents a standard Brownian motionWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
under a risk-neutral
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
probability measure and
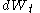its differentialDifferential (mathematics)
In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
. Other than Rendleman–Bartter and Ho–Lee, which do not capture the mean reversion
Mean reversion
Mean reversion is a mathematical concept sometimes used for stock investing, but it can be applied to other assets. In general terms, the essence of the concept is the assumption that both a stock's high and low prices are temporary and that a stock's price will tend to move to the average price...
of interest rates, these models can be thought of as specific cases of Ornstein–Uhlenbeck processes. Where the model is lognormal, a variable
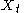, is assumed to follow an Ornstein–Uhlenbeck process and 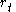is assumed to follow . Ho-Lee and subsequent models can be calibrated to market data, meaning that these can exactly return the price of bonds comprising the yield curve.- Merton'sRobert C. MertonRobert Carhart Merton is an American economist, Nobel laureate in Economics, and professor at the MIT Sloan School of Management.-Biography:...
Model (1973) models the short rate as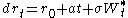
: where 
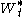is a one-dimensional Brownian motion under the spot martingale measure. - The Vasicek modelVasicek modelIn finance, the Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of "one-factor model" as it describes interest rate movements as driven by only one source of market risk...
(1977) models the short rate as
- The Rendleman–Bartter model (1980) models the short rate as
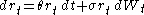
- The Cox–Ingersoll–Ross model (1985) supposes
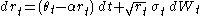
- The Ho–Lee model (1986) models the short rate as
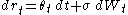
- The Hull–White model (1990) - also called the extended Vasicek model - posits
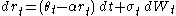. In many presentations one or more of the parameters 
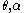and 
are not time-dependent. The model may also be applied as lognormal. - The Black–Derman–Toy model (1990) has
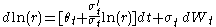for time-dependent short rate volatility and 
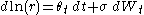otherwise; the model is lognormal. - The Black–Karasinski modelBlack–Karasinski modelIn financial mathematics, the Black–Karasinski model is a mathematical model of the term structure of interest rates; see short rate model. It is a one-factor model as it describes interest rate movements as driven by a single source of randomness....
(1991), which is lognormal, has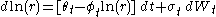
; the model may be seen as the lognormal application of Hull-White.http://php.portals.mbs.ac.uk/Portals/49/docs/spoon/IRD/Ch5_ShortRateNOTE.pdf - The Kalotay–Williams–Fabozzi model (1993) has the short rate as
, a lognormal analogue to the Ho–Lee model, and a special case of the Black–Derman–Toy model.
Multi-factor short-rate models
Besides the above one-factor models, there are also multi-factor models of the short rate, among them the best known are the LongstaffFrancis Longstaff
Francis A. Longstaff is the Allstate Professor of Insurance and Finance at the Anderson School of Management, University of California, Los Angeles, and the current Finance Area Chair....
and Schwartz
Eduardo Schwartz
Eduardo Saul Schwartz is a professor of finance at the Anderson School of Management, University of California, Los Angeles, where he holds the California Chair in Real Estate & Land Economics...
two factor model and the Chen three factor model (also called "stochastic mean and stochastic volatility model"):
- The Longstaff–Schwartz model (1992) supposes the short rate dynamics are given by:
, 
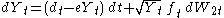, where the short rate is defined as 
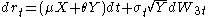. - The Chen modelChen modelIn finance, the Chen model is a mathematical model describing the evolution of interest rates. It is a type of "three-factor model" as it describes interest rate movements as driven by three sources of market risk...
(1996) which has a stochastic mean and volatility of the short rate, is given by :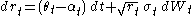
, 
, 
.
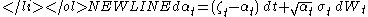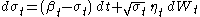Other interest rate models
The other major framework for interest rate modelling is the Heath–Jarrow–Morton framework (HJM). Unlike the short rate models described above, this class of models is generally non-Markovian. This makes general HJM models computationally intractable for most purposes. The great advantage of HJM models is that they give an analytical description of the entire yield curve, rather than just the short rate. For some purposes (e.g., valuation of mortgage backed securities), this can be a big simplification. The Cox–Ingersoll–Ross and Hull–White models in one or more dimensions can both be straightforwardly expressed in the HJM framework. Other short rate models do not have any simple dual HJM representation.
The HJM framework with multiple sources of randomness, including as it does the Brace–Gatarek–Musiela model and market models, is often preferred for models of higher dimension.