
Binomial options pricing model
Encyclopedia
In finance
, the binomial options pricing model (BOPM) provides a generalizable numerical method
for the valuation of options
. The binomial model was first proposed by Cox
, Ross
and Rubinstein
in 1979. Essentially, the model uses a “discrete-time” (lattice based
) model of the varying price over time of the underlying
financial instrument. In general, binomial options pricing models do not have closed-form solutions.
).
Although computationally slower than the Black–Scholes formula, it is more accurate, particularly for longer-dated options on securities with dividend
payments. For these reasons, various versions of the binomial model are widely used by practitioners in the options markets.
For options with several sources of uncertainty (e.g., real option
s) and for options with complicated features (e.g., Asian option
s), binomial methods are less practical due to several difficulties, and Monte Carlo option model
s are commonly used instead. When simulating a small number of time steps Monte Carlo simulation will be more computationally time-consuming than BOPM (cf. Monte Carlo methods in finance
). However, the worst-case runtime of BOPM will be O(2n), where n is the number of time steps in the simulation. Monte Carlo simulations will generally have a polynomial time complexity, and will be faster for large numbers of simulation steps.
Valuation is performed iteratively, starting at each of the final nodes (those that may be reached at the time of expiration), and then working backwards through the tree towards the first node (valuation date). The value computed at each stage is the value of the option at that point in time.
Option valuation using this method is, as described, a three-step process:
At each step, it is assumed that the underlying instrument will move up or down by a specific factor ( or
or 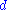 ) per step of the tree (where, by definition,
) per step of the tree (where, by definition,  and
and 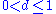 ). So, if
). So, if 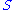 is the current price, then in the next period the price will either be
is the current price, then in the next period the price will either be  or
or  .
.
The up and down factors are calculated using the underlying volatility
, , and the time duration of a step,
, and the time duration of a step,  , measured in years (using the day count convention
, measured in years (using the day count convention
of the underlying instrument). From the condition that the variance
of the log of the price is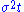 , we have:
, we have:
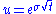
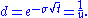
The above is the original Cox, Ross, & Rubinstein (CRR) method; there are other techniques for generating the lattice, such as "the equal probabilities" tree. The Trinomial tree
is a similar model, allowing for an up, down or stable path.
The CRR method ensures that the tree is recombinant, i.e. if the underlying asset moves up and then down (u,d), the price will be the same as if it had moved down and then up (d,u) — here the two paths merge or recombine. This property reduces the number of tree nodes, and thus accelerates the computation of the option price.
This property also allows that the value of the underlying asset at each node can be calculated directly via formula, and does not require that the tree be built first. The node-value will be: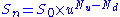
Where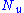 is the number of up ticks and
is the number of up ticks and  is the number of down ticks.
is the number of down ticks.
, or exercise, value.
Where is the strike price
is the strike price
and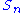 is the spot price of the underlying asset at the
is the spot price of the underlying asset at the 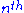 period.
period.
In overview: the “binomial value” is found at each node, using the risk neutrality
assumption; see Risk neutral valuation. If exercise is permitted at the node, then the model takes the greater of binomial and exercise value at the node.
The steps are as follows:
(1) Under the risk neutrality assumption, today's fair price
of a derivative
is equal to the expected value
of its future payoff discounted by the risk free rate
. Therefore, expected value is calculated using the option values from the later two nodes (Option up and Option down) weighted by their respective probabilities—“probability” p of an up move in the underlying, and “probability” (1-p) of a down move. The expected value is then discounted at r, the risk free rate
corresponding to the life of the option.

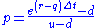 is chosen such that the related binomial distribution simulates the geometric Brownian motion
is chosen such that the related binomial distribution simulates the geometric Brownian motion
of the underlying stock with parameters r and σ,
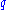 is the dividend yield
is the dividend yield
of the underlying corresponding to the life of the option. It follows that in a risk-neutral world futures price should have an expected growth rate of zero and therefore we can consider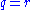 for futures.
for futures.
(2) This result is the “Binomial Value”. It represents the fair price of the derivative at a particular point in time (i.e. at each node), given the evolution in the price of the underlying to that point. It is the value of the option if it were to be held—as opposed to exercised at that point.
(3) Depending on the style of the option, evaluate the possibility of early exercise at each node: if (1) the option can be exercised, and (2) the exercise value exceeds the Binomial Value, then (3) the value at the node is the exercise value.
In calculating the value at the next time step calculated—i.e. one step closer to valuation—the model must use the value selected here, for “Option up”/“Option down” as appropriate, in the formula at the node.
The following algorithm
demonstrates the approach computing the price of an American put option, although is easily generalized for calls and for European and Bermudan options:
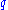 , in the formula above can lead to significant mis-pricing of the option near an ex-dividend date. Instead, it is common to model dividends as discrete payments on the anticipated future ex-dividend dates.
, in the formula above can lead to significant mis-pricing of the option near an ex-dividend date. Instead, it is common to model dividends as discrete payments on the anticipated future ex-dividend dates.
To model discrete dividend payments in the binomial model, apply the following rule:
In 2011, Georgiadis shows that the binomial options pricing model has a lower bound on complexity that rules out a closed-form solution.
Other tree structures
Fixed income derivatives, Don M. Chance
Online
Desktop
Programming languages
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, the binomial options pricing model (BOPM) provides a generalizable numerical method
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
for the valuation of options
Option (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
. The binomial model was first proposed by Cox
John C. Cox
John Carrington Cox is the Nomura Professor of Finance at the MIT Sloan School of Management. He is one of the world's leading experts on options theory and one of the inventors of the Cox–Ross–Rubinstein model for option pricing, as well as of the Cox–Ingersoll–Ross model for interest rate dynamics...
, Ross
Stephen Ross (economist)
Stephen Alan "Steve" Ross is the inaugural Franco Modigliani Professor of Financial Economics at the MIT Sloan School of Management. He is known for initiating several important theories and models in financial economics...
and Rubinstein
Mark Rubinstein
Mark Edward Rubinstein is a leading financial economist and financial engineer. He is currently Professor of Finance at the Haas School of Business of the University of California, Berkeley, where he is involved in teaching courses in the , an academic program that is focused on equipping...
in 1979. Essentially, the model uses a “discrete-time” (lattice based
Lattice model (finance)
In finance, a lattice model can be used to find the fair value of a stock option; variants also exist for interest rate derivatives.The model divides time between now and the option's expiration into N discrete periods...
) model of the varying price over time of the underlying
Underlying
In finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
financial instrument. In general, binomial options pricing models do not have closed-form solutions.
Use of the model
The Binomial options pricing model approach is widely used as it is able to handle a variety of conditions for which other models cannot easily be applied. This is largely because the BOPM is based on the description of an underlying instrument over a period of time rather than a single point. As a consequence, it is used to value American options that are exercisable at any time in a given interval as well as Bermudan options that are exercisable at specific instances of time. Being relatively simple, the model is readily implementable in computer software (including a spreadsheetSpreadsheet
A spreadsheet is a computer application that simulates a paper accounting worksheet. It displays multiple cells usually in a two-dimensional matrix or grid consisting of rows and columns. Each cell contains alphanumeric text, numeric values or formulas...
).
Although computationally slower than the Black–Scholes formula, it is more accurate, particularly for longer-dated options on securities with dividend
Dividend
Dividends are payments made by a corporation to its shareholder members. It is the portion of corporate profits paid out to stockholders. When a corporation earns a profit or surplus, that money can be put to two uses: it can either be re-invested in the business , or it can be distributed to...
payments. For these reasons, various versions of the binomial model are widely used by practitioners in the options markets.
For options with several sources of uncertainty (e.g., real option
Real option
Real options valuation, also often termed Real options analysis, applies option valuation techniques to capital budgeting decisions. A real option itself, is the right — but not the obligation — to undertake some business decision; typically the option to make, abandon, expand, or contract a...
s) and for options with complicated features (e.g., Asian option
Asian option
An Asian option is a special type of option contract. For Asian options the payoff is determined by the average underlying price over some pre-set period of time...
s), binomial methods are less practical due to several difficulties, and Monte Carlo option model
Monte Carlo option model
In mathematical finance, a Monte Carlo option model uses Monte Carlo methods to calculate the value of an option with multiple sources of uncertainty or with complicated features....
s are commonly used instead. When simulating a small number of time steps Monte Carlo simulation will be more computationally time-consuming than BOPM (cf. Monte Carlo methods in finance
Monte Carlo methods in finance
Monte Carlo methods are used in finance and mathematical finance to value and analyze instruments, portfolios and investments by simulating the various sources of uncertainty affecting their value, and then determining their average value over the range of resultant outcomes. This is usually done...
). However, the worst-case runtime of BOPM will be O(2n), where n is the number of time steps in the simulation. Monte Carlo simulations will generally have a polynomial time complexity, and will be faster for large numbers of simulation steps.
Methodology
The binomial pricing model traces the evolution of the option's key underlying variables in discrete-time. This is done by means of a binomial lattice (tree), for a number of time steps between the valuation and expiration dates. Each node in the lattice represents a possible price of the underlying at a given point in time.Valuation is performed iteratively, starting at each of the final nodes (those that may be reached at the time of expiration), and then working backwards through the tree towards the first node (valuation date). The value computed at each stage is the value of the option at that point in time.
Option valuation using this method is, as described, a three-step process:
- price tree generation,
- calculation of option value at each final node,
- sequential calculation of the option value at each preceding node.
STEP 1: Create the binomial price tree
The tree of prices is produced by working forward from valuation date to expiration.At each step, it is assumed that the underlying instrument will move up or down by a specific factor (
 or
or 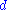 ) per step of the tree (where, by definition,
) per step of the tree (where, by definition,  and
and 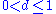 ). So, if
). So, if 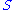 is the current price, then in the next period the price will either be
is the current price, then in the next period the price will either be  or
or  .
.The up and down factors are calculated using the underlying volatility
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
,
 , and the time duration of a step,
, and the time duration of a step,  , measured in years (using the day count convention
, measured in years (using the day count conventionDay count convention
In finance, a day count convention determines how interest accrues over time for a variety of investments, including bonds, notes, loans, mortgages, medium-term notes, swaps, and forward rate agreements . This determines the amount transferred on interest payment dates, and also the calculation of...
of the underlying instrument). From the condition that the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the log of the price is
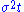 , we have:
, we have: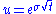
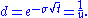
The above is the original Cox, Ross, & Rubinstein (CRR) method; there are other techniques for generating the lattice, such as "the equal probabilities" tree. The Trinomial tree
Trinomial Tree
The Trinomial tree is a lattice based computational model used in financial mathematics to price options. It was developed by Phelim Boyle in 1986. It is an extension of the Binomial options pricing model, and is conceptually similar...
is a similar model, allowing for an up, down or stable path.
The CRR method ensures that the tree is recombinant, i.e. if the underlying asset moves up and then down (u,d), the price will be the same as if it had moved down and then up (d,u) — here the two paths merge or recombine. This property reduces the number of tree nodes, and thus accelerates the computation of the option price.
This property also allows that the value of the underlying asset at each node can be calculated directly via formula, and does not require that the tree be built first. The node-value will be:
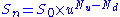
Where
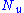 is the number of up ticks and
is the number of up ticks and  is the number of down ticks.
is the number of down ticks.STEP 2: Find Option value at each final node
At each final node of the tree — i.e. at expiration of the option — the option value is simply its intrinsicOption time value
In finance, the time value of an option is the premium a rational investor would pay over its current exercise value , based on its potential to increase in value before expiring. This probability is always greater than zero, thus an option is always worth more than its current exercise value...
, or exercise, value.
- Max [ (
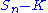 ), 0 ], for a call optionCall optionA call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller...
), 0 ], for a call optionCall optionA call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller... - Max [ (
 –
– 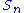 ), 0 ], for a put optionPut optionA put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
), 0 ], for a put optionPut optionA put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
:
Where
 is the strike price
is the strike priceStrike price
In options, the strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the spot price of the underlying instrument at that time.Formally, the strike...
and
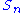 is the spot price of the underlying asset at the
is the spot price of the underlying asset at the 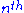 period.
period.STEP 3: Find Option value at earlier nodes
Once the above step is complete, the option value is then found for each node, starting at the penultimate time step, and working back to the first node of the tree (the valuation date) where the calculated result is the value of the option.In overview: the “binomial value” is found at each node, using the risk neutrality
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
assumption; see Risk neutral valuation. If exercise is permitted at the node, then the model takes the greater of binomial and exercise value at the node.
The steps are as follows:
(1) Under the risk neutrality assumption, today's fair price
Fair value
Fair value, also called fair price , is a concept used in accounting and economics, defined as a rational and unbiased estimate of the potential market price of a good, service, or asset, taking into account such objective factors as:* acquisition/production/distribution costs, replacement costs,...
of a derivative
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
is equal to the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of its future payoff discounted by the risk free rate
Risk-free interest rate
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
. Therefore, expected value is calculated using the option values from the later two nodes (Option up and Option down) weighted by their respective probabilities—“probability” p of an up move in the underlying, and “probability” (1-p) of a down move. The expected value is then discounted at r, the risk free rate
Risk-free interest rate
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
corresponding to the life of the option.
- The following formula to compute the expectation value is applied at each node:
- Binomial Value = [ p × Option up + (1-p) × Option down] × exp (- r × Δt), or

- where
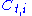 is the option's value for the
is the option's value for the 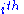 node at time
node at time  ,
,
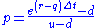 is chosen such that the related binomial distribution simulates the geometric Brownian motion
is chosen such that the related binomial distribution simulates the geometric Brownian motionGeometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
of the underlying stock with parameters r and σ,
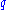 is the dividend yield
is the dividend yieldDividend yield
The dividend yield or the dividend-price ratio on a company stock is the company's total annual dividend payments divided by its market capitalization, or the dividend per share, divided by the price per share. It is often expressed as a percentage...
of the underlying corresponding to the life of the option. It follows that in a risk-neutral world futures price should have an expected growth rate of zero and therefore we can consider
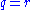 for futures.
for futures.- Note that for
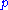 to be in the interval
to be in the interval 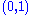 the following condition on
the following condition on  has to be satisfied
has to be satisfied 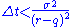 .
.
(2) This result is the “Binomial Value”. It represents the fair price of the derivative at a particular point in time (i.e. at each node), given the evolution in the price of the underlying to that point. It is the value of the option if it were to be held—as opposed to exercised at that point.
(3) Depending on the style of the option, evaluate the possibility of early exercise at each node: if (1) the option can be exercised, and (2) the exercise value exceeds the Binomial Value, then (3) the value at the node is the exercise value.
- For a European option, there is no option of early exercise, and the binomial value applies at all nodes.
- For an American option, since the option may either be held or exercised prior to expiry, the value at each node is: Max (Binomial Value, Exercise Value).
- For a Bermudan option, the value at nodes where early exercise is allowed is: Max (Binomial Value, Exercise Value); at nodes where early exercise is not allowed, only the binomial value applies.
In calculating the value at the next time step calculated—i.e. one step closer to valuation—the model must use the value selected here, for “Option up”/“Option down” as appropriate, in the formula at the node.
The following algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
demonstrates the approach computing the price of an American put option, although is easily generalized for calls and for European and Bermudan options:
function americanPut(T, S, K, r, sigma, q, n) {
' T... expiration time
' S... stock price
' K... strike price
' n... height of the binomial tree
deltaT := T / n;
up := exp(sigma * sqrt(deltaT));
p0 := (up * exp(-r * deltaT) - exp(-q * deltaT)) * up / (up^2 - 1);
p1 := exp(-r * deltaT) - p0;
' initial values at time T
for i := 0 to n {
p[i] := K - S * up^(2*i - n);
if p[i] < 0 then p[i] := 0;
}
' move to earlier times
for j := n-1 down to 0 {
for i := 0 to j {
p[i] := p0 * p[i] + p1 * p[i+1]; ' binomial value
exercise := K - S * up^(2*i - j); ' exercise value
if p[i] < exercise then p[i] := exercise;
}
}
return americanPut := p[0];
}
Discrete dividends
In practice, the use of continuous dividend yield,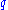 , in the formula above can lead to significant mis-pricing of the option near an ex-dividend date. Instead, it is common to model dividends as discrete payments on the anticipated future ex-dividend dates.
, in the formula above can lead to significant mis-pricing of the option near an ex-dividend date. Instead, it is common to model dividends as discrete payments on the anticipated future ex-dividend dates.To model discrete dividend payments in the binomial model, apply the following rule:
- At each time step,
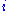 , calculate
, calculate  , for all
, for all  where
where  is the present value of the
is the present value of the 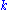 -th dividend. Subtract this value from the value of the security price
-th dividend. Subtract this value from the value of the security price 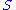 at each node (
at each node ( ,
, 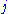 ).
).
Relationship with Black–Scholes
Similar assumptions underpin both the binomial model and the Black–Scholes model, and the binomial model thus provides a discrete time approximation to the continuous process underlying the Black–Scholes model. In fact, for European options without dividends, the binomial model value converges on the Black–Scholes formula value as the number of time steps increases. The binomial model assumes that movements in the price follow a binomial distribution; for many trials, this binomial distribution approaches the normal distribution assumed by Black–Scholes. In addition, when analyzed as numerical procedure, the CRR binomial method can be viewed as a special case of explicit finite difference method for Black–Scholes PDE.In 2011, Georgiadis shows that the binomial options pricing model has a lower bound on complexity that rules out a closed-form solution.
See also
- Trinomial treeTrinomial TreeThe Trinomial tree is a lattice based computational model used in financial mathematics to price options. It was developed by Phelim Boyle in 1986. It is an extension of the Binomial options pricing model, and is conceptually similar...
—a similar model with three possible paths per node. - Tree (data structure)Tree (data structure)In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
- Black–Scholes: binomial lattices are able to handle a variety of conditions for which Black–Scholes cannot be applied.
- Monte Carlo option modelMonte Carlo option modelIn mathematical finance, a Monte Carlo option model uses Monte Carlo methods to calculate the value of an option with multiple sources of uncertainty or with complicated features....
, used in the valuation of options with complicated features that make them difficult to value through other methods. - Real options analysisReal options analysisReal options valuation, also often termed Real options analysis, applies option valuation techniques to capital budgeting decisions. A real option itself, is the right — but not the obligation — to undertake some business decision; typically the option to make, abandon, expand, or contract a...
—where the BOPM is widely used. - Quantum financeQuantum FinanceQuantum finance is an interdisciplinary research field, applying theories and methods developed by quantum physicists and economists in order to solve problems in finance. It is a type of Econophysics.- Background on instrument pricing:...
—quantum binomial pricing model. - Mathematical financeMathematical financeMathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, which has a list of related articles.
Discussion
- The Binomial Model for Pricing Options, Prof. Thayer Watkins
- Using The Binomial Model to Price Derivatives, Quantnotes
- Binomial Method (Cox, Ross, Rubinstein), global-derivatives.com
- Binomial Option Pricing (PDF), Prof. Robert M. Conroy
- The Binomial Option Pricing Model, Simon Benninga and Zvi Wiener
- Options pricing using a binomial lattice, The Investment Analysts Society of Southern AfricaInvestment Analysts Society of Southern AfricaThe Investment Analyst's Society of Southern Africa is the liaison body for the financial analyst profession in South Africa. It is based in Johannesburg South Africa, with members from Cape Town, Durban and throughout the region.-Membership:...
, Prof. Don M. Chance - Some notes on the Cox-Ross-Rubinstein binomial model for pricing an option, Prof. Rob Thompson
- Binomial Option Pricing Model by Fiona Maclachlan, The Wolfram Demonstrations Project
- On the Irrelevance of Expected Stock Returns in the Pricing of Options in the Binomial Model: A Pedagogical Note by Valeri Zakamouline
Variations
American and Bermudan options- Pricing Bermudan Options, umanitoba.ca
- Option Pricing: Extending the Basic Binomial Model, Rich Tanenbaum
Other tree structures
- Extending and simulating the quantum binomial options pricing model, Keith Meyer
- A Synthesis of Binomial Option Pricing Models for Lognormally Distributed Assets, Don M. Chance
- Binomial and Trinomial Trees - overview, The Quant Equation Archive, sitmo.com
Fixed income derivatives, Don M. Chance
- Binomial Models for Fixed Income Analytics, David Backus
- Binomial Term Structure Models, Simon Benninga and Zvi Wiener
Computer implementations
Spreadsheets- American Options - Binomial Method, global-derivatives.com
- European Options - Binomial Method, global-derivatives.com
Online
- European and American Option Trees, Jan-Petter Janssen
Desktop
- FairmatFairmatFairmat is a free-of-charge multi-platform software that allows to model financial contracts or projects with many contingencies by decomposing it into basic parts. Complex structures and dependencies are modeled using a graphical interface...
, free-to-use software which implements various binomial trees option pricing through a plug-in.
Programming languages

