Trinomial Tree
Encyclopedia
The Trinomial tree is a lattice based
computational model
used in financial mathematics to price options
. It was developed by Phelim Boyle
in 1986. It is an extension of the Binomial options pricing model
, and is conceptually similar. It can also be shown that the approach is equivalent to the explicit finite difference method for option pricing
.
stock price is modeled as a recombining tree, where, at each node the price has three possible paths: an up, down and stable or middle path. These values are found by multiplying the value at the current node by the appropriate factor
, 
or 
where
(the structure is recombining)
and the corresponding probabilities are:
.
In the above formulae:
is the length of time per step in the tree and is simply time to maturity divided by the number of time steps; 
is the risk-free interest rate
over this maturity;
is the corresponding volatility of the underlying
;
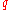is its corresponding dividend yield
.
As with the binomial model, these factors and probabilities are specified so as to ensure that the price of the underlying
evolves as a martingale
, while the moments
are matched approximately (and with increasing accuracy for smaller time-steps).
Once the tree of prices has been calculated, the option price is found at each node largely as for the binomial model, by working backwards from the final nodes to today. The difference being that the option value at each non-final node is determined based on the three - as opposed to two - later nodes and their corresponding probabilities. The model is best understood visually - see, for example Trinomial Tree Option Calculator (Peter Hoadley).
If the length of time-steps
is taken as an exponentially distributed random variable and interpreted as the waiting time between two movements of the stock price then the resulting stochastic process is a birth-death process
. The resulting model is soluble and there exist analytic pricing and hedging formulae for various options.
s the trinomial model (or adaptations) is sometimes more stable and accurate, regardless of step-size.
Lattice model (finance)
In finance, a lattice model can be used to find the fair value of a stock option; variants also exist for interest rate derivatives.The model divides time between now and the option's expiration into N discrete periods...
computational model
Computational model
A computational model is a mathematical model in computational science that requires extensive computational resources to study the behavior of a complex system by computer simulation. The system under study is often a complex nonlinear system for which simple, intuitive analytical solutions are...
used in financial mathematics to price options
Option (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
. It was developed by Phelim Boyle
Phelim Boyle
Phelim Boyle , a distinguished professor and actuary, is a professor of finance in the Laurier School of Business & Economics at Wilfrid Laurier University in Canada and is a pioneer of quantitative finance. He is best known for initiating the use of Monte Carlo methods in option pricing...
in 1986. It is an extension of the Binomial options pricing model
Binomial options pricing model
In finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
, and is conceptually similar. It can also be shown that the approach is equivalent to the explicit finite difference method for option pricing
Finite difference methods for option pricing
Finite difference methods for option pricing are numerical methods used in mathematical finance for the valuation of options. Finite difference methods were first applied to option pricing by Eduardo Schwartz in 1977....
.
Formula
Under the trinomial method, the underlyingUnderlying
In finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
stock price is modeled as a recombining tree, where, at each node the price has three possible paths: an up, down and stable or middle path. These values are found by multiplying the value at the current node by the appropriate factor
, or where (the structure is recombining)and the corresponding probabilities are:
.In the above formulae:
is the length of time per step in the tree and is simply time to maturity divided by the number of time steps; is the risk-free interest rateRisk-free interest rate
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
over this maturity;
is the corresponding volatility of the underlyingVolatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
;
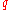is its corresponding dividend yieldDividend yield
The dividend yield or the dividend-price ratio on a company stock is the company's total annual dividend payments divided by its market capitalization, or the dividend per share, divided by the price per share. It is often expressed as a percentage...
.
As with the binomial model, these factors and probabilities are specified so as to ensure that the price of the underlying
Underlying
In finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
evolves as a martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
, while the moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
are matched approximately (and with increasing accuracy for smaller time-steps).
Once the tree of prices has been calculated, the option price is found at each node largely as for the binomial model, by working backwards from the final nodes to today. The difference being that the option value at each non-final node is determined based on the three - as opposed to two - later nodes and their corresponding probabilities. The model is best understood visually - see, for example Trinomial Tree Option Calculator (Peter Hoadley).
If the length of time-steps
is taken as an exponentially distributed random variable and interpreted as the waiting time between two movements of the stock price then the resulting stochastic process is a birth-death processBirth-death process
The birth–death process is a special case of continuous-time Markov process where the states represent the current size of a population and where the transitions are limited to births and deaths...
. The resulting model is soluble and there exist analytic pricing and hedging formulae for various options.
Application
The trinomial model is considered to produce more accurate results than the binomial model when fewer time steps are modelled, and is therefore used when computational speed or resources may be an issue. For vanilla options, as the number of steps increases, the results rapidly converge, and the binomial model is then preferred due to its simpler implementation. For exotic optionExotic option
In finance, an exotic option is a derivative which has features making it more complex than commonly traded products . These products are usually traded over-the-counter , or are embedded in structured notes....
s the trinomial model (or adaptations) is sometimes more stable and accurate, regardless of step-size.
See also
- Binomial options pricing modelBinomial options pricing modelIn finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
- Valuation of optionsValuation of optionsIn finance, a price is paid or received for purchasing or selling options. This price can be split into two components.These are:* Intrinsic Value* Time Value-Intrinsic Value:...
- Option: Model implementation
- Korn-Kreer-Lenssen Model
External links
- Phelim BoylePhelim BoylePhelim Boyle , a distinguished professor and actuary, is a professor of finance in the Laurier School of Business & Economics at Wilfrid Laurier University in Canada and is a pioneer of quantitative finance. He is best known for initiating the use of Monte Carlo methods in option pricing...
, 1986. "Option Valuation Using a Three-Jump Process", International Options Journal 3, 7-12. - Ralf Korn, Markus Kreer and Mark Lenssen: "Pricing of european options when the underlying stock price follows a linear birth-death process", Stochastic Models Vol. 14(3), 1998, pp 647 – 662