
Normal order
Encyclopedia
In quantum field theory
a product of quantum fields, or equivalently their creation and annihilation operators
, is usually said to be normal ordered (also called Wick order) when all creation operators are to the left of all annihilation operators in the product. The process of putting a product into normal order is called normal ordering (also called Wick ordering). The terms antinormal order and antinormal ordering are analogously defined, where the annihilation operators are placed to the left of the creation operators.
Normal ordering of a product quantum fields or creation and annihilation operators
can also be defined in many other ways. Which definition is most appropriate depends on the expectation values needed for a given calculation. Most of this article uses the most common definition of normal ordering, that given above, which is appropriate when taking expectation values using the vacuum state of the creation and annihilation operators
.
The process of normal ordering is particularly important for a quantum mechanical
Hamiltonian
. When quantizing a classical
Hamiltonian there is some freedom when choosing the operator order, and these choices lead to differences in the ground state
energy
.
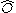 denotes an arbitrary operator, then the normal ordered form of
denotes an arbitrary operator, then the normal ordered form of 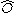 is denoted by
is denoted by  .
.
An alternative notation involves placing the operator inside two colons denoted by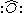
These satisfy the commutator
relationship

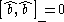
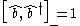
where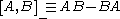 denotes the commutator
denotes the commutator
. We may rewrite the last one as: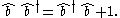
 :
:
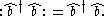
The expression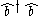 has not been changed because it is already in normal order - the creation operator
has not been changed because it is already in normal order - the creation operator 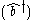 is already to the left of the annihilation operator
is already to the left of the annihilation operator 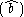 .
.
2. A more interesting example is the normal ordering of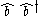 :
: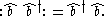
Here the normal ordering operation has reordered the terms by placing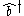 to the left of
to the left of 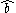 .
.
These two results can be combined with the commutation relation obeyed by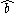 and
and 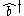 to get
to get
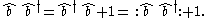
or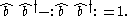
This equation is used in defining the contractions used in Wick's theorem
.
3. An example with multiple operators is:
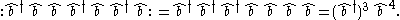
4. A more complicated example shows how we can normal order functions of operators by expanding them out in a series
and normal ordering each term:
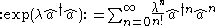
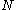 different bosons there are
different bosons there are 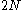 operators:
operators:
Here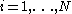 .
.
These satisfy the commutation relations: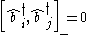
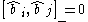

where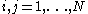 and
and 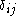 denotes the Kronecker delta.
denotes the Kronecker delta.
These may be rewritten as: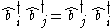
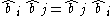
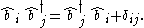
 ) we have
) we have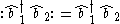
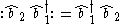
2. For three different bosons ( ) we have
) we have
Notice that since (by the commutation relations)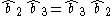 the order in which we write the annihilation operators does not matter.
the order in which we write the annihilation operators does not matter.
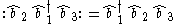
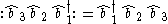
. We will now examine the normal ordering of fermionic creation and annihilation operator products.
These satisfy the anticommutator relationships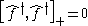
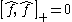
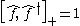
where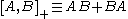 denotes the anticommutator. These may be rewritten as
denotes the anticommutator. These may be rewritten as
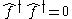
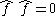

To define the normal ordering of a product of fermionic creation and annihilation operators we must take into account the number of interchanges between neighbouring operators. We get a minus sign for each such interchange.
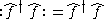
This expression is already in normal order so nothing is changed.
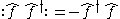
Here we introduce a minus sign because we have changed the order of two operators.
These can be combined, along with the anticommutation relations, to show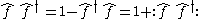
or
This equation, which is in the same form as the bosonic case above, is used in defining the contractions used in Wick's theorem
.
2. The normal order of any more complicated cases gives zero because there will be at least one creation or annihilation operator appearing twice. For example: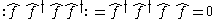
 different fermions there are
different fermions there are  operators:
operators:
Here .
.
These satisfy the commutation relations: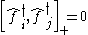
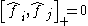
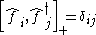
where and
and 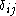 denotes the Kronecker delta.
denotes the Kronecker delta.
These may be rewritten as: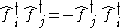
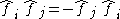
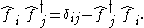
When calculating the normal order of products of fermion operators we must take into account the number of interchanges of neighbouring operators required to rearrange the expression. It is as if we pretend the creation and annihilation operators anticommute and then we reorder the expression to ensure the creation operators are on the left and the annihilation operators are on the right - all the time taking account of the anticommutation relations.
 ) we have
) we have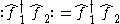
Here the expression is already normal ordered so nothing changes.
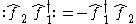
Here we introduce a minus sign because we have interchanged the order of two operators.
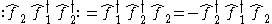
Note that the order in which we write the operators here, unlike in the bosonic case, does matter.
2. For three different fermions (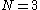 ) we have
) we have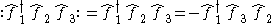
Notice that since (by the anticommutation relations)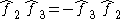 the order in which we write the operators does matter in this case.
the order in which we write the operators does matter in this case.
Similarly we have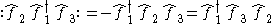
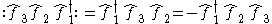
of a normal ordered product of creation and annihilation operators is zero. This is because, denoting the vacuum state
by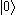 , the creation and annihilation operators satisfy
, the creation and annihilation operators satisfy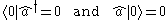
(here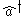 and
and 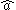 are creation and annihilation operators (either bosonic or fermionic)).
are creation and annihilation operators (either bosonic or fermionic)).
Any normal ordered operator therefore has a vacuum expectation value of zero. Although an operator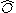 may satisfy
may satisfy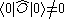
we always have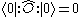
This is particularly useful when defining a quantum mechanical Hamiltonian
. If the Hamiltonian of a theory is in normal order then the ground state energy will be zero:
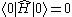 .
.
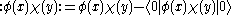
where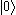 is again the vacuum state. Each of the two terms on the right hand side typically blows up in the limit as y approaches x but the difference between them has a well-defined limit. This allows us to define :φ(x)χ(x):.
is again the vacuum state. Each of the two terms on the right hand side typically blows up in the limit as y approaches x but the difference between them has a well-defined limit. This allows us to define :φ(x)χ(x):.

(with contractions).
This theorem provides a simple method for computing vacuum expectation values of operators. This theorem was the reason normal ordering was defined in the first place.
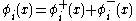 .
.
In a product of fields, the fields are split into the two parts and the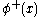 parts are moved so as to be always to the left of all the
parts are moved so as to be always to the left of all the 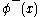 parts. In the usual case considered in the rest of the article, the
parts. In the usual case considered in the rest of the article, the 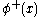 contains only creation operators, while the
contains only creation operators, while the  contains only annihilation operators. As this is a mathematical identity, one can split fields in any way one likes. However for this to be a useful procedure one demands that the normal ordered product of any combination of fields has zero expectation value
contains only annihilation operators. As this is a mathematical identity, one can split fields in any way one likes. However for this to be a useful procedure one demands that the normal ordered product of any combination of fields has zero expectation value
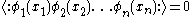
It is also important for practical calculations that all the commutators (anti-commutator for fermionic fields) of all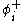 and
and 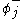 are all c-numbers. These two properties means that we can apply Wick's theorem in the usual way, turning expectation values of time-ordered products of fields into products of c-cumber pairs, the contractions. In this generalised setting, the contraction is defined to be the difference between the time-ordered product and the normal ordered product of a pair of fields.
are all c-numbers. These two properties means that we can apply Wick's theorem in the usual way, turning expectation values of time-ordered products of fields into products of c-cumber pairs, the contractions. In this generalised setting, the contraction is defined to be the difference between the time-ordered product and the normal ordered product of a pair of fields.
The simplest example is found in the context of Thermal quantum field theory
(Evans and Steer 1996). In this case the expectation values of interest are statistical ensembles, traces over all states weighted by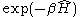 . For instance, for a single bosonic quantum harmonic oscillator we have that the thermal expectation value of the number operator is simply the Bose-Einstein distribution
. For instance, for a single bosonic quantum harmonic oscillator we have that the thermal expectation value of the number operator is simply the Bose-Einstein distribution
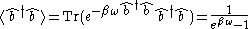
So here the number operator is normal ordered in the usual sense used in the rest of the article yet its thermal expectation values are non-zero. Applying Wick's theorem and doing calculation with the usual normal ordering in this thermal context is possible but computationally impractical. The solution is to define a different ordering, such that the
is normal ordered in the usual sense used in the rest of the article yet its thermal expectation values are non-zero. Applying Wick's theorem and doing calculation with the usual normal ordering in this thermal context is possible but computationally impractical. The solution is to define a different ordering, such that the 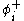 and
and 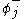 are linear combinations of the original annihilation and creations operators. The combinations are chosen to ensure that the thermal expectation values of normal ordered products are always zero so the split chosen will depend on the temperature.
are linear combinations of the original annihilation and creations operators. The combinations are chosen to ensure that the thermal expectation values of normal ordered products are always zero so the split chosen will depend on the temperature.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
a product of quantum fields, or equivalently their creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
, is usually said to be normal ordered (also called Wick order) when all creation operators are to the left of all annihilation operators in the product. The process of putting a product into normal order is called normal ordering (also called Wick ordering). The terms antinormal order and antinormal ordering are analogously defined, where the annihilation operators are placed to the left of the creation operators.
Normal ordering of a product quantum fields or creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
can also be defined in many other ways. Which definition is most appropriate depends on the expectation values needed for a given calculation. Most of this article uses the most common definition of normal ordering, that given above, which is appropriate when taking expectation values using the vacuum state of the creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
.
The process of normal ordering is particularly important for a quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
. When quantizing a classical
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
Hamiltonian there is some freedom when choosing the operator order, and these choices lead to differences in the ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
.
Notation
If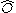 denotes an arbitrary operator, then the normal ordered form of
denotes an arbitrary operator, then the normal ordered form of 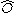 is denoted by
is denoted by  .
.An alternative notation involves placing the operator inside two colons denoted by
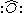
Bosons
Bosons are particles which satisfy Bose-Einstein statistics. We will now examine the normal ordering of bosonic creation and annihilation operator products.Single bosons
If we start with only one type of boson there are two operators of interest:-
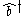 : the boson's creation operator.
: the boson's creation operator. -
 : the boson's annihilation operator.
: the boson's annihilation operator.
These satisfy the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
relationship

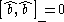
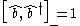
where
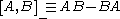 denotes the commutator
denotes the commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
. We may rewrite the last one as:
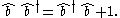
Examples
1. We'll consider the simplest case first. This is the normal ordering of :
: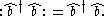
The expression
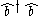 has not been changed because it is already in normal order - the creation operator
has not been changed because it is already in normal order - the creation operator 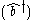 is already to the left of the annihilation operator
is already to the left of the annihilation operator 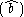 .
.2. A more interesting example is the normal ordering of
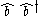 :
: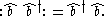
Here the normal ordering operation has reordered the terms by placing
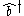 to the left of
to the left of 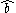 .
.These two results can be combined with the commutation relation obeyed by
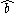 and
and 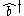 to get
to get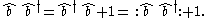
or
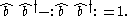
This equation is used in defining the contractions used in Wick's theorem
Wick's theorem
Wick's theorem is a method of reducing high-order derivatives to a combinatorics problem . It is named after Gian-Carlo Wick. It is used extensively in quantum field theory to reduce arbitrary products of creation and annihilation operators to sums of products of pairs of these operators...
.
3. An example with multiple operators is:
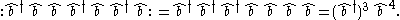
4. A more complicated example shows how we can normal order functions of operators by expanding them out in a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
and normal ordering each term:
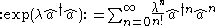
Multiple bosons
If we now consider different bosons there are
different bosons there are  operators:
operators:
-
 : the
: the 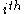 boson's creation operator.
boson's creation operator. -
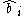 : the
: the 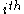 boson's annihilation operator.
boson's annihilation operator.
Here
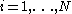 .
.These satisfy the commutation relations:
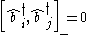
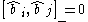

where
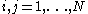 and
and 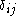 denotes the Kronecker delta.
denotes the Kronecker delta.These may be rewritten as:
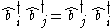
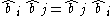
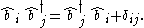
Examples
1. For two different bosons ( ) we have
) we have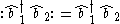
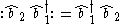
2. For three different bosons (
 ) we have
) we have
Notice that since (by the commutation relations)
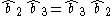 the order in which we write the annihilation operators does not matter.
the order in which we write the annihilation operators does not matter.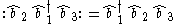
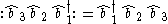
Fermions
Fermions are particles which satisfy Fermi-Dirac statisticsFermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
. We will now examine the normal ordering of fermionic creation and annihilation operator products.
Single fermions
For a single fermion there are two operators of interest:-
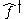 : the fermion's creation operator.
: the fermion's creation operator. -
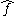 : the fermion's annihilation operator.
: the fermion's annihilation operator.
These satisfy the anticommutator relationships
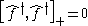
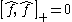
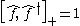
where
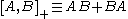 denotes the anticommutator. These may be rewritten as
denotes the anticommutator. These may be rewritten as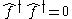
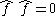

To define the normal ordering of a product of fermionic creation and annihilation operators we must take into account the number of interchanges between neighbouring operators. We get a minus sign for each such interchange.
Examples
1. We again start with the simplest cases: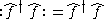
This expression is already in normal order so nothing is changed.
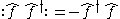
Here we introduce a minus sign because we have changed the order of two operators.
These can be combined, along with the anticommutation relations, to show
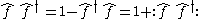
or

This equation, which is in the same form as the bosonic case above, is used in defining the contractions used in Wick's theorem
Wick's theorem
Wick's theorem is a method of reducing high-order derivatives to a combinatorics problem . It is named after Gian-Carlo Wick. It is used extensively in quantum field theory to reduce arbitrary products of creation and annihilation operators to sums of products of pairs of these operators...
.
2. The normal order of any more complicated cases gives zero because there will be at least one creation or annihilation operator appearing twice. For example:
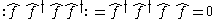
Multiple fermions
For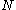 different fermions there are
different fermions there are  operators:
operators:
-
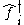 : the
: the 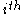 fermion's creation operator.
fermion's creation operator. -
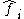 : the
: the 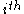 fermion's annihilation operator.
fermion's annihilation operator.
Here
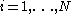 .
.These satisfy the commutation relations:
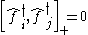
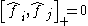
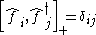
where
 and
and 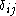 denotes the Kronecker delta.
denotes the Kronecker delta.These may be rewritten as:
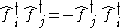
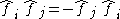
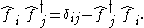
When calculating the normal order of products of fermion operators we must take into account the number of interchanges of neighbouring operators required to rearrange the expression. It is as if we pretend the creation and annihilation operators anticommute and then we reorder the expression to ensure the creation operators are on the left and the annihilation operators are on the right - all the time taking account of the anticommutation relations.
Examples
1. For two different fermions ( ) we have
) we have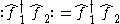
Here the expression is already normal ordered so nothing changes.
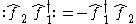
Here we introduce a minus sign because we have interchanged the order of two operators.
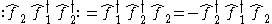
Note that the order in which we write the operators here, unlike in the bosonic case, does matter.
2. For three different fermions (
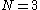 ) we have
) we have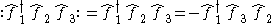
Notice that since (by the anticommutation relations)
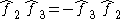 the order in which we write the operators does matter in this case.
the order in which we write the operators does matter in this case.Similarly we have
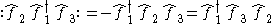
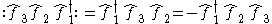
Uses in quantum field theory
The vacuum expectation valueVacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of a normal ordered product of creation and annihilation operators is zero. This is because, denoting the vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
by
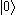 , the creation and annihilation operators satisfy
, the creation and annihilation operators satisfy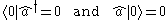
(here
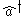 and
and 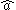 are creation and annihilation operators (either bosonic or fermionic)).
are creation and annihilation operators (either bosonic or fermionic)).Any normal ordered operator therefore has a vacuum expectation value of zero. Although an operator
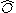 may satisfy
may satisfy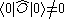
we always have
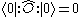
This is particularly useful when defining a quantum mechanical Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
. If the Hamiltonian of a theory is in normal order then the ground state energy will be zero:
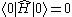 .
.Free fields
With two free fields φ and χ,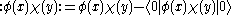
where
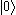 is again the vacuum state. Each of the two terms on the right hand side typically blows up in the limit as y approaches x but the difference between them has a well-defined limit. This allows us to define :φ(x)χ(x):.
is again the vacuum state. Each of the two terms on the right hand side typically blows up in the limit as y approaches x but the difference between them has a well-defined limit. This allows us to define :φ(x)χ(x):.Wick's theorem
Wick's theorem states that:
(with contractions).
This theorem provides a simple method for computing vacuum expectation values of operators. This theorem was the reason normal ordering was defined in the first place.
Alternative definitions
The most general definition of normal ordering involves splitting all quantum fields into two parts (for example see Evans and Steer 1996)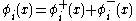 .
.In a product of fields, the fields are split into the two parts and the
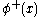 parts are moved so as to be always to the left of all the
parts are moved so as to be always to the left of all the 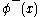 parts. In the usual case considered in the rest of the article, the
parts. In the usual case considered in the rest of the article, the 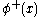 contains only creation operators, while the
contains only creation operators, while the  contains only annihilation operators. As this is a mathematical identity, one can split fields in any way one likes. However for this to be a useful procedure one demands that the normal ordered product of any combination of fields has zero expectation value
contains only annihilation operators. As this is a mathematical identity, one can split fields in any way one likes. However for this to be a useful procedure one demands that the normal ordered product of any combination of fields has zero expectation value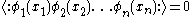
It is also important for practical calculations that all the commutators (anti-commutator for fermionic fields) of all
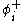 and
and 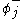 are all c-numbers. These two properties means that we can apply Wick's theorem in the usual way, turning expectation values of time-ordered products of fields into products of c-cumber pairs, the contractions. In this generalised setting, the contraction is defined to be the difference between the time-ordered product and the normal ordered product of a pair of fields.
are all c-numbers. These two properties means that we can apply Wick's theorem in the usual way, turning expectation values of time-ordered products of fields into products of c-cumber pairs, the contractions. In this generalised setting, the contraction is defined to be the difference between the time-ordered product and the normal ordered product of a pair of fields.The simplest example is found in the context of Thermal quantum field theory
Thermal quantum field theory
In theoretical physics, thermal quantum field theory or finite temperature field theory is a set of methods to calculate expectation values of physical observables of a quantum field theory at finite temperature....
(Evans and Steer 1996). In this case the expectation values of interest are statistical ensembles, traces over all states weighted by
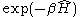 . For instance, for a single bosonic quantum harmonic oscillator we have that the thermal expectation value of the number operator is simply the Bose-Einstein distribution
. For instance, for a single bosonic quantum harmonic oscillator we have that the thermal expectation value of the number operator is simply the Bose-Einstein distributionBose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
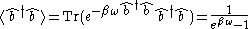
So here the number operator
 is normal ordered in the usual sense used in the rest of the article yet its thermal expectation values are non-zero. Applying Wick's theorem and doing calculation with the usual normal ordering in this thermal context is possible but computationally impractical. The solution is to define a different ordering, such that the
is normal ordered in the usual sense used in the rest of the article yet its thermal expectation values are non-zero. Applying Wick's theorem and doing calculation with the usual normal ordering in this thermal context is possible but computationally impractical. The solution is to define a different ordering, such that the 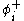 and
and 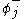 are linear combinations of the original annihilation and creations operators. The combinations are chosen to ensure that the thermal expectation values of normal ordered products are always zero so the split chosen will depend on the temperature.
are linear combinations of the original annihilation and creations operators. The combinations are chosen to ensure that the thermal expectation values of normal ordered products are always zero so the split chosen will depend on the temperature.

