
Ishimori equation
Encyclopedia
The Ishimori equation is a partial differential equation
proposed by the Japanese mathematician
. Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable
.

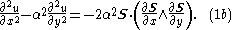
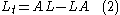
of the equation is given by
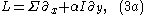

Here
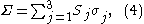
the are the Pauli matrices
are the Pauli matrices
and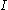 is the identity matrix.
is the identity matrix.
in 1+1 dimensions it reduces to the continuous classical Heisenberg ferromagnet equation
(CCHFE). The CCHFE is integrable.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
proposed by the Japanese mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
. Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
.
Equation
The IE has the form
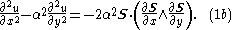
Lax representation
The Lax representation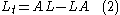
of the equation is given by
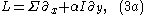

Here
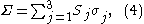
the
 are the Pauli matrices
are the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
and
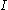 is the identity matrix.
is the identity matrix.Reductions
IE admits an important reduction:in 1+1 dimensions it reduces to the continuous classical Heisenberg ferromagnet equation
Heisenberg model (classical)
The Classical Heisenberg model is the n = 3 case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena.-Definition:...
(CCHFE). The CCHFE is integrable.
Equivalent counterpart
The equivalent counterpart of the IE is the Davey-Stewartson equation.See also
- Nonlinear Schrödinger equationNonlinear Schrödinger equationIn theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
- Heisenberg model (classical)Heisenberg model (classical)The Classical Heisenberg model is the n = 3 case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena.-Definition:...
- Spin waveSpin waveSpin waves are propagating disturbances in the ordering of magnetic materials. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are boson modes of the spin lattice...
- Landau-Lifshitz equation
- SolitonSolitonIn mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
- VortexVortexA vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
- Nonlinear systems
- Davey–Stewartson equationDavey–Stewartson equationIn fluid dynamics, the Davey–Stewartson equation was introduced in a paper by to describe the evolution of a three-dimensional wave-packet on water of finite depth....
External links
- Ishimori_system at the dispersive equations wiki

