
Inverse scattering transform
Encyclopedia
In mathematics
, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years. The method is a non-linear analogue of the Fourier transform
, which itself can be applied to solve many linear partial differential equations.
The inverse scattering transform may be applied to many of the so-called exactly solvable models, that is to say completely integrable infinite dimensional systems. These include the Korteweg–de Vries equation
, the nonlinear Schrödinger equation
, the coupled nonlinear Schrödinger equations, the Sine-Gordon equation
, the Kadomtsev–Petviashvili equation, the Toda lattice equation, the Ishimori equation
, the Dym equation etc. A further, particularly interesting, family of examples is provided by the Bogomolny equations (for a given gauge group and oriented Riemannian 3-fold), the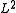 solutions of which are magnetic monopoles.
solutions of which are magnetic monopoles.
A characteristic of solutions obtained by the inverse scattering method is the existence of solitons which have no analogue for linear partial differential equations. The term "soliton" arises from non-linear optics.
The inverse scattering problem can be written as a Riemann–Hilbert factorization problem. This formulation can be generalized to differential operators of order greater than 2 and also to periodic potentials.
for a function
u; of two real
variables, one space variable x and one time variable t :
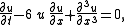
with and
and 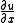 denoting partial derivative
denoting partial derivative
s with respect to t and x.
To solve the initial value problem for this equation where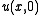 is a known function of x, one associates to this equation the Schrödinger eigenvalue equation
is a known function of x, one associates to this equation the Schrödinger eigenvalue equation
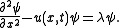
where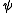 is an unknown function of t and x and u is the solution of the Korteweg–de Vries equation that is unknown except at
is an unknown function of t and x and u is the solution of the Korteweg–de Vries equation that is unknown except at 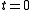 . The constant
. The constant 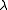 is an eigenvalue.
is an eigenvalue.
From the Schrödinger equation we obtain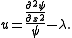
Substituting this into the Korteweg–de Vries equation and integrating gives the equation
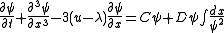
where C and D are constants.
of the situation being studied.
Step 2. Employ forward scattering. This consists in finding the Lax pair
. The Lax pair consists of two linear operators,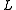 and
and 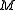 , such that
, such that 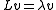 and
and 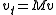 , where the subscript t in
, where the subscript t in 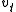 denotes the time derivative of
denotes the time derivative of  . It is extremely important that the eigenvalue
. It is extremely important that the eigenvalue 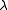 be independent of time; i.e.
be independent of time; i.e. 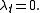 Necessary and sufficient conditions for this to occur are determined as follows: take the time derivative
Necessary and sufficient conditions for this to occur are determined as follows: take the time derivative
of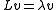 to obtain
to obtain

Plugging in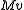 for
for 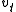 yields
yields
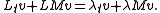
Rearranging on the far right term gives us
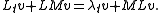
Thus,
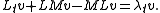
Since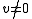 , this implies that
, this implies that 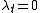 if and only if
if and only if
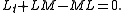
This is Lax's equation. One important thing to note about Lax's equation is that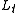 is the time derivative of
is the time derivative of 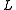 precisely where it explicitly depends on
precisely where it explicitly depends on  . The reason for defining the differentiation this way is motivated by the simplest instance of
. The reason for defining the differentiation this way is motivated by the simplest instance of  , which is the Schrödinger operator (see Schrödinger equation
, which is the Schrödinger operator (see Schrödinger equation
):

where u is the "potential". Comparing the expression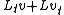 with
with 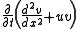 shows us that
shows us that 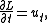 thus ignoring the first term.
thus ignoring the first term.
After concocting the appropriate Lax pair it should be the case that Lax's equation recovers the original nonlinear PDE.
Step 3. Determine the time evolution of the eigenfunctions associated to each eigenvalue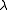 , the norming constants, and the reflection coefficient, all three comprising the so-called scattering data. This time evolution is given by a system of linear ordinary differential equations which can be solved.
, the norming constants, and the reflection coefficient, all three comprising the so-called scattering data. This time evolution is given by a system of linear ordinary differential equations which can be solved.
Step 4. Perform the inverse scattering procedure by solving the Gelfand–Levitan–Marchenko integral equation (Israel Moiseevich Gelfand and Boris Moiseevich Levitan; Vladimir Aleksandrovich Marchenko), a linear integral equation
, to obtain the final solution of the original nonlinear PDE. All the scattering data is required in order to do this. Note that if the reflection coefficient is zero, the process becomes much easier. Note also that this step works if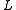 is a differential or difference operator of order two, but not necessarily for higher orders. In all cases however, the inverse scattering problem is reducible to a Riemann–Hilbert factorization problem.
is a differential or difference operator of order two, but not necessarily for higher orders. In all cases however, the inverse scattering problem is reducible to a Riemann–Hilbert factorization problem.
(See Ablowitz-Clarkson (1991) for either approach. See Marchenko (1986) for a mathematical rigorous treatment.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years. The method is a non-linear analogue of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, which itself can be applied to solve many linear partial differential equations.
The inverse scattering transform may be applied to many of the so-called exactly solvable models, that is to say completely integrable infinite dimensional systems. These include the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
, the nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
, the coupled nonlinear Schrödinger equations, the Sine-Gordon equation
Sine-Gordon equation
The sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
, the Kadomtsev–Petviashvili equation, the Toda lattice equation, the Ishimori equation
Ishimori equation
The Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .-Equation:The IE has the form...
, the Dym equation etc. A further, particularly interesting, family of examples is provided by the Bogomolny equations (for a given gauge group and oriented Riemannian 3-fold), the
 solutions of which are magnetic monopoles.
solutions of which are magnetic monopoles.A characteristic of solutions obtained by the inverse scattering method is the existence of solitons which have no analogue for linear partial differential equations. The term "soliton" arises from non-linear optics.
The inverse scattering problem can be written as a Riemann–Hilbert factorization problem. This formulation can be generalized to differential operators of order greater than 2 and also to periodic potentials.
Example: the Korteweg–de Vries equation
The Korteweg–de Vries equation is a nonlinear, dispersive, evolution partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
u; of two real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables, one space variable x and one time variable t :
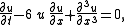
with
 and
and 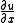 denoting partial derivative
denoting partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s with respect to t and x.
To solve the initial value problem for this equation where
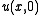 is a known function of x, one associates to this equation the Schrödinger eigenvalue equation
is a known function of x, one associates to this equation the Schrödinger eigenvalue equation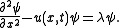
where
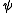 is an unknown function of t and x and u is the solution of the Korteweg–de Vries equation that is unknown except at
is an unknown function of t and x and u is the solution of the Korteweg–de Vries equation that is unknown except at 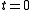 . The constant
. The constant 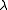 is an eigenvalue.
is an eigenvalue.From the Schrödinger equation we obtain
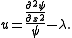
Substituting this into the Korteweg–de Vries equation and integrating gives the equation
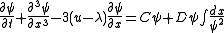
where C and D are constants.
Method of solution
Step 1. Determine the nonlinear partial differential equation. This is usually accomplished by analyzing the physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
of the situation being studied.
Step 2. Employ forward scattering. This consists in finding the Lax pair
Lax pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
. The Lax pair consists of two linear operators,
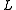 and
and 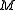 , such that
, such that 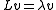 and
and 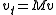 , where the subscript t in
, where the subscript t in 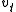 denotes the time derivative of
denotes the time derivative of  . It is extremely important that the eigenvalue
. It is extremely important that the eigenvalue 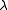 be independent of time; i.e.
be independent of time; i.e. 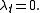 Necessary and sufficient conditions for this to occur are determined as follows: take the time derivative
Necessary and sufficient conditions for this to occur are determined as follows: take the time derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of
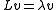 to obtain
to obtain
Plugging in
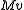 for
for 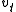 yields
yields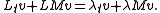
Rearranging on the far right term gives us
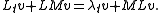
Thus,
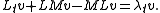
Since
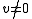 , this implies that
, this implies that 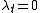 if and only if
if and only ifIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
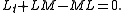
This is Lax's equation. One important thing to note about Lax's equation is that
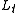 is the time derivative of
is the time derivative of 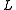 precisely where it explicitly depends on
precisely where it explicitly depends on  . The reason for defining the differentiation this way is motivated by the simplest instance of
. The reason for defining the differentiation this way is motivated by the simplest instance of  , which is the Schrödinger operator (see Schrödinger equation
, which is the Schrödinger operator (see Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
):

where u is the "potential". Comparing the expression
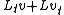 with
with 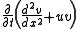 shows us that
shows us that 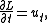 thus ignoring the first term.
thus ignoring the first term.After concocting the appropriate Lax pair it should be the case that Lax's equation recovers the original nonlinear PDE.
Step 3. Determine the time evolution of the eigenfunctions associated to each eigenvalue
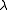 , the norming constants, and the reflection coefficient, all three comprising the so-called scattering data. This time evolution is given by a system of linear ordinary differential equations which can be solved.
, the norming constants, and the reflection coefficient, all three comprising the so-called scattering data. This time evolution is given by a system of linear ordinary differential equations which can be solved.Step 4. Perform the inverse scattering procedure by solving the Gelfand–Levitan–Marchenko integral equation (Israel Moiseevich Gelfand and Boris Moiseevich Levitan; Vladimir Aleksandrovich Marchenko), a linear integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
, to obtain the final solution of the original nonlinear PDE. All the scattering data is required in order to do this. Note that if the reflection coefficient is zero, the process becomes much easier. Note also that this step works if
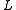 is a differential or difference operator of order two, but not necessarily for higher orders. In all cases however, the inverse scattering problem is reducible to a Riemann–Hilbert factorization problem.
is a differential or difference operator of order two, but not necessarily for higher orders. In all cases however, the inverse scattering problem is reducible to a Riemann–Hilbert factorization problem.(See Ablowitz-Clarkson (1991) for either approach. See Marchenko (1986) for a mathematical rigorous treatment.)
List of integrable equations
- Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
- nonlinear Schrödinger equationNonlinear Schrödinger equationIn theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
- Camassa-Holm equation
- Sine-Gordon equationSine-Gordon equationThe sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
- Toda lattice
- Ishimori equationIshimori equationThe Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .-Equation:The IE has the form...
- Dym equation and so on.

